支持向量机实现兵王问题的分类(Python问题)

问题分析

本文是基于浙江大学机器学习课程的兵王问题进行Python实现，虽然胡老师提供了Python代码，但是我觉得这个代码还是Matlab思想，没有Python的特点。因此对于这个问题重新进行编程。下面先对问题进行简单的分析，如果觉得我没讲清楚的可以戳下面的链接看胡老师对于这个问题的分析:
课程链接
在国际象棋中，存在着一种残局的现象。剩余三子，分别是黑方的王，白方的王和兵，那么无论这三子在棋盘的布局如何，只有两种结果，白方胜利和逼和。这就是一个二分类问题。

数据分布

关于这个问题的数据集krkopt.DATA可以在老师给的代码里面找到，然后老师也推荐了一个网址UCI Meachine Learning这个网址挺棒的，但是我没在里面找到老师说的那个数据集，大家可以去试试。
先给大家看一下，数据的一些形式：

老师说，前面六个就是棋子的位置，draw就是逼和，后面的数字six就代表，白棋最少用六步就能将死对方。然后呢，可以看一下最后一个有几种情况：

这里和老师讲的有点出入，因为老师并没有讲到zreo这个选项，这里也是我比较困惑的一点：

但是还是就是按照老师这个样子分类，并敲代码。
下面就是我的代码。

我的代码

import pandas as pd
from sklearn.model_selection import train_test_split,cross_val_score
from sklearn.svm import SVC
from sklearn.metrics import confusion_matrix,roc_curve,auc
import seaborn as sns
import matplotlib.pyplot as plt
# 读取数据
data = pd.read_csv('krkopt.DATA',header=None)
data.dropna(inplace=True)
# 将样本数值化
for i in [0,2,4]:
    data.loc[data[i]=='a',i] = 1
    data.loc[data[i]=='b',i] = 2
    data.loc[data[i]=='c',i] = 3
    data.loc[data[i]=='d',i] = 4
    data.loc[data[i]=='e',i] = 5
    data.loc[data[i]=='f',i] = 6
    data.loc[data[i]=='g',i] = 7
    data.loc[data[i]=='h',i] = 8
# 将标签数值化
data.loc[data[6]!='draw',6] = -1    
data.loc[data[6]=='draw',6] = 1
# 归一化处理
for i in range(6):
    data[i] = (data[i]-data[i].mean())/data[i].std()  
# 拆分训练集和测试集
X_train, X_test, y_train, y_test =  train_test_split(data.iloc[:,:6],data[6],test_size=0.82178500142572)
# 寻找C和gamma的粗略范围
CScale = [i for i in range(100,201,10)];
gammaScale = [i/10 for i in range(1,11)];
cv_scores = 0
for i in CScale:
    for j in gammaScale:
        model = SVC(kernel = 'rbf', C = i,gamma=j)
        scores = cross_val_score(model,X_train, y_train,cv =5,scoring = 'accuracy')
        if scores.mean()>cv_scores:
            cv_scores = scores.mean()
            savei = i
            savej = j*100
# 找到更精确的C和gamma
CScale = [i for i in range(savei-5,savei+5)];
gammaScale = [i/100+0.01 for i in range(int(savej)-5,int(savej)+5)];
cv_scores = 0
for i in CScale:
    for j in gammaScale:
        model = SVC(kernel = 'rbf', C = i,gamma=j)
        scores = cross_val_score(model,X_train, y_train,cv =5,scoring = 'accuracy')
        if scores.mean()>cv_scores:
            cv_scores = scores.mean()
            savei = i
            savej = j
#将确定好的参数重新建立svm模型
model = SVC(kernel = 'rbf', C=savei,gamma=savej)
model.fit(X_train, y_train)
pre = model.predict(X_test)
model.score(X_test,y_test)
# 绘制AUC和EER图形
cm = confusion_matrix(y_test, pre, labels=[-1, 1], sample_weight=None)
sns.set()
f,ax=plt.subplots()
sns.heatmap(cm,annot=True,ax=ax) #画热力图
ax.set_title('confusion matrix') #标题
ax.set_xlabel('predict') #x轴
ax.set_ylabel('true') #y轴
fpr,tpr,threshold = roc_curve(y_test, pre) ###计算真正率和假正率
roc_auc = auc(fpr,tpr) ###计算auc的值，auc就是曲线包围的面积，越大越好
plt.figure()
lw = 2
plt.figure(figsize=(10,10))
plt.plot(fpr, tpr, color='darkorange',lw=lw, label='ROC curve (area = %0.2f)' % roc_auc) ###假正率为横坐标，真正率为纵坐标做曲线
plt.plot([0, 1], [1, 0], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

结果

老师用Matlab得到的结果是99.61%，那么上述程序的正确率为99.53%，可以看到差距不是很大，而且呢就算是同一个程序得到的结果可能也会有差距，这是因为划分测试集和训练集的不同造成的。

对于上述的评价指标我还画出了混淆矩阵：

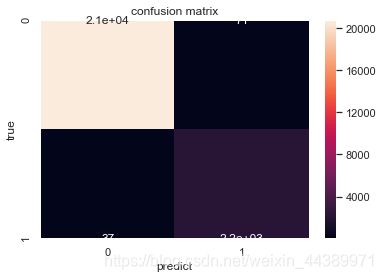
AUC和EER曲线：

auc是指黄色曲线和x轴的面积，eer是指蓝色曲线与黄色曲线的交点的横坐标，衡量一个系统的好坏就在于auc越大，性能越好，eer越小性能越好。

反思

由于Python对于绘制AUC是用折线图的而且是系统自带的库，就是就比较不美观，而且计算eer的值也不是很方便，只能通过肉眼进行估计。那么最后，就是这个代码依旧有改进的空间，如果各位有兴趣的话，可以进行讨论，有错误的话也可以指出。