工业大数据在对焊机的应用

        笔者在年初做了一个项目，这个项目比较特殊，客户的需求是：通过数据建模证明现有的设备工艺参数区间是合理的。现将主要过程进行复盘。

        一、客户： 客户是一家生产汽车启停电池的公司

        二、项目背景：客户准备给一家汽车主机厂供电池，在供应商准入前，主机厂来客户公司验厂，其中对焊是关键工序，主机厂要求客户给出有理有据的说法来证明现有工艺的合理性。比如“初始电压”参数的区间是3~3.5，那么就要说明这个[3~3.5]是科学合理的，而不是通过经验得到的。

        三、设备：TBS对焊机（德国进口）

        四、工艺：工艺过程简单来说，是让两极柱通过瞬间电流，接触点产生高温使铅合金熔化，然后冷却连接在一起，本质上来说是个焊接工序。该工序的质量对电池质量有较大的影响。

        五、工艺参数：设备PLC能控制的参数包括：开始电压、焊接间距、对接时间、脉冲、焊接电流、冷却时间、IC时间、实际功率、实际电流、实际电阻、传感器电压；

        无法直接采集到的数据包括：对焊液压、冷却水流量、环境温湿度、焊件存放时间、极柱合金关键元素百分比

       

        六、建模思路：

        1、数据采集，一部分是通过读取PLC数据，一部分是靠人工目视记录；收集一个月的数据。

        本项目数据采集和其他项目不同的地方在于：本次数据是由数采和人工采集共同完成，并且借鉴了“田口正交实验法”、按照“每个变量因子均匀改变，其他变量不变，使得变量对电阻的影响更加准确客观”的思路采集数据

        2、特征工程，变量太少，而且每一个都非常有用，没有必要做特征工程

        3、对焊工艺好坏的标准依据实际电阻，如果该值在工艺区间内（125±5），则该电池对焊质量合格；经过与现场工艺人员沟通，将最重要的变量做了筛选，最终建模的自变量和因变量如下：

                自变量X：开始电压、焊接间距、焊接时间、脉冲、冷却时间、总电压、对焊液压、冷却水流量

                因变量Y：实际电阻

        4、通过神经网络拟合f(x)=y的模型

下面是Python构建神经网络模型代码：

import matplotlib.pyplot as plt
from math import sqrt
from matplotlib import pyplot
import pandas as pd
from numpy import concatenate
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from tensorflow.keras.optimizers import Adam
from sklearn.model_selection import train_test_split
from keras.callbacks import EarlyStopping
import tensorflow as tf
from tensorflow import keras
from keras.models import load_model

dataset = pd.read_csv(r'C:\Users\Think\Desktop\dhj0418.csv')
scaler = MinMaxScaler(feature_range=(0, 1))
data=dataset.iloc[:,0:9]
scaled = scaler.fit_transform(data)
Y = scaled[:, -1]
X = scaled[:, 0:-1]
train_x, test_x, train_y, test_y = train_test_split(X, Y, test_size=0.2)

model = Sequential() 
input = X.shape[1]
model.add(Dense(128, input_shape=(input,)))
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(128, input_shape=(input,)))
model.add(Activation('relu'))
model.add(Dense(128, input_shape=(input,)))
model.add(Activation('relu'))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer=Adam())
early_stopping = EarlyStopping(monitor='val_loss', patience=50, verbose=2)

history = model.fit(train_x, train_y, epochs=350,batch_size=20,
                    validation_data=(test_x, test_y), verbose=2,
                    shuffle=False, callbacks=[early_stopping])

pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.title('Model loss')
pyplot.ylabel('Loss')
pyplot.xlabel('Epoch')
pyplot.legend()
pyplot.show()

yhat = model.predict(test_x)
# 预测y 逆标准化
inv_yhat0 = concatenate((test_x, yhat), axis=1)
inv_yhat1 = scaler.inverse_transform(inv_yhat0)
inv_yhat = inv_yhat1[:, -1]
# 原始y逆标准化
test_y = test_y.reshape(len(test_y), 1)
inv_y0 = concatenate((test_x, test_y), axis=1)
inv_y1 = scaler.inverse_transform(inv_y0)
inv_y = inv_y1[:, -1]



# 计算RMSE
rmse = sqrt(mean_squared_error(inv_y, inv_yhat))
print('Test RMSE: %.3f' % rmse)
plt.plot(inv_y)
plt.plot(inv_yhat)
plt.show()

通过数次建模，最优模型的RMSE=3（标准电阻是125，相当于模型的准确度在正负3左右），用此模型作为下面证明过程的模型

        七、论证逻辑：

        这一步是整个项目最重要的环节，即如何能够证明工艺参数的合理性。这个问题直接证明比较复杂，我用的是归纳法和反证法的思路：如果工艺区间是合理的，那么它必须解释三个问题

        1、工艺参数区间是否能使质量指标靠近目标值？

        2、工艺参数区间对应的质量是否稳定？

        3、是否有其他更优的参数区间？

        八、论证过程：

        每个参数都有对应的区间范围，本文只以“初始电压”这个参数为例，其他参数方法相同

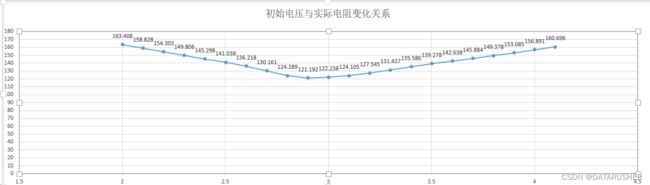
        1、初始电压的工艺文件标定的范围是[2.7~3.3]，将这个区间拆开成一维数组[2.7,2.8,2.9,3,3.1,3.2,3.3],再将数组每个元素代入进6.4构建的网络模型（其他变量不变）中，求出对应电阻，形成一个电阻变化曲线

从结果可以看出，区间[2.7-3.3]对应的电阻范围是[121-131]，是符合工艺要求的。因此能解释7.1“工艺参数区间是否能使质量指标靠近目标值”

        2、从上图可以看出初始电压从区间[2-4]对应的电阻，将初始电压分为三个区间[2-2.6]         [2.7- 3.3] [3.3-4],计算每个区间对应电阻标准差。

        初始电压 [2-2.6]    电阻标准差3.8

        初始电压 [2.7-3.3]    电阻标准差1.42

        初始电压 [3.3-4]    电阻标准差3

        工艺区间 [2.7-3.3] 对应电阻标准差最小，说明此区间内电阻波动小，波动小因此而稳定，因此可以解释7.2“工艺参数区间对应的质量是否稳定”

        3、将初始电压作为唯一的变量代入神经网络模型，求每个值对应的函数的偏导数，偏导数越小，说明该值对应的质量波动越小，即该参数是较优参数；但是神经网络是一个很复杂的网络结构，很难直接求函数偏导数；所以这里借鉴了蒙特卡洛模拟思想求近似偏导。对神经网络抽样，具体过程如下：初始电压记为X，X的变化率设为0.0001，电阻记为Y

∂X/∂Y=ΔY/ΔX|x=xi

ΔY=f(2.1)-f(2)   f(x)为上文构建的神经网络模型

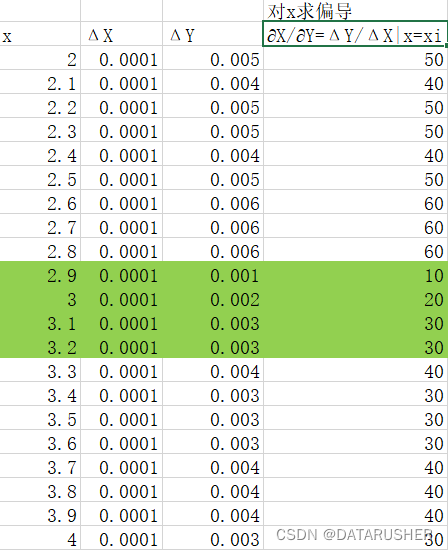
通过抽样20个样本得到以下数据

 从数据中可以看出，变化率最小的区间为[2.9-3.2],此区间正好是在工艺区间中，且没有更优区间因此可以解释7.3“是否有其他更优的参数区间”

至此，第七部分的三个问题都能解释，最终能够证明-初始电压的参数区间[2.7-3.3]是最优区间。

并且在此基础上能给出更优化的区间为[2.9-3.2]

        九、项目后续：

        跟客户汇报后，客户对论证过程比较认可，但是还是有一些问题。

        

        数据问题

        1、有很多关键参数无法自动采集，比如冷却水流量、焊件存放时间。这类数据只能目视采集

        2、生产计划不足，设备开几天后又停几天

        3、由于上述两个问题，间接导致数量样本不够，跑出来的模型精度可能不高

        无法反应多变量之间的关系

        1、参数论证无法同时分析多个参数的影响，未来如果有类似项目，这个问题是要解决的

        这个项目案例中，如果能获取到足够多的数据，还可以做更深的应用：比如分析某些质量异常的原因。这类问题用常规的思路不好解决，但是通过数据挖掘可以找到一些规律指导工艺员排查；