Machine Learning with Python Cookbook 学习笔记 第1章

Machine Learning with Python Cookbook 学习笔记 第1章

前言

• 本笔记是针对人工智能典型算法的课程中Machine Learning with Python Cookbook的学习笔记
• 学习的实战代码都放在代码压缩包中
• 实战代码的运行环境是python3.9 numpy 1.23.1 **anaconda 4.12.0 **
• 代码和笔记将会存放到仓库https://github.com/yy6768/Machine-Learning-with-Python-Cookbook-notebook中

Chapter 1 Vectors, Matrices, and Arrays

vector（向量）

matrice(矩阵)

array（数组）

1.0 简介

• numpy是python机器学习的基础
• 它可以对机器学习常用的数据结构进行操作
• 操作支持向量矩阵和数组

numpy相关资料：

NumPy 教程 | 菜鸟教程 (runoob.com)

1.1 创建一个vector

Problem

You need to create a vector

Solution

Use Numpy to create a one-dimensional array

在numpy中一维数组等价于向量

numpy.array函数

numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)

vectorExample.py

# 引入numpy库
import numpy as np

# 创建行向量
vector_row = np.array([1, 2, 3])

# 创建列向量
vector_column = np.array([[1],
                          [2],
                          [3]])

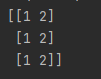
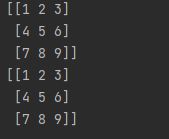
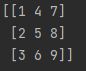
分别打印两者结果如下

1.2 创建一个矩阵

Problem

You need to create a matrix.

Solution

Use Numpy to create a two-dimensional array:

创建二维数组=矩阵

matrixExample.py

# 导入库
import numpy as np

# 创建一个 matrix
matrix = np.array([[1, 2],
                   [1, 2],
                   [1, 2]])

打印matrix如下

两个原因不推荐适用matrix

• First, arrays are the de facto standard data structure of NumPy.（数组是numpy标准的数据结构）
• Second the vast majority of NumPy operations return arrays, not matrix object.(大部分numpy的标准操作返回的是array)

1.3 Creating a Sparse Matrix（创建一个稀疏矩阵）

Sparse：稀疏

Problem

Given data with very few nonzero values, you want to efficiently represent it.

Solution

Create a sparse matrix:

sparseMatrixExample.py

import numpy as np
# 引入sparse
from scipy import sparse

# 创建一个矩阵
matrix = np.array([[0, 0],
                  [0, 1],
                  [3, 0]])

# create compressed sparse row (CSR) matrix
matrix_sparse = sparse.csr_matrix(matrix)

# view sparse matrix
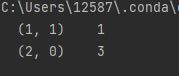
print(matrix_sparse)

打印结果

scipy库

• 需要额外安装，是一个开源的python高级科学计算库

  pip install scipy
  

• 额外支持的操作包括：数值积分、最优化、统计和一些专用函数

• 学习资源：SciPy 教程 | 菜鸟教程 (runoob.com)

Discussion

• A frequent situation in machine learning is having a huge amount of data; however most of the elements in the data are zeros. 机器学习中大多情形拥有大量数据但是数据很多时候为0

• Sparse matricies only store nonzero elements and assume all other values will be zero, leading to significant computational savings. 稀疏矩阵存储非零值并且假设其他值是0，从而节约计算量

• 稀疏矩阵的存储方式：CSR，存储非0坐标位置

  Compressed Sparse Row（CSR）——稀疏矩阵的存储格式 - 知乎 (zhihu.com)

# create larger matrix
matrix_large = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
                         [3, 0, 0, 0, 0, 0, 0, 0, 0, 0]])

# create compressed sparse row (CSR) matrix
matrix_large_sparse = sparse.csr_matrix(matrix_large)

# view original sparse matrix
print(matrix_sparse)

打印结果：

• 稀疏矩阵中0元素的添加不会影响其在存储中所占的空间
• 稀疏矩阵有许多类型：compressed sparse column, list of lists, and dictionary of keys

1.4 Selected Elements

Problem

You need to select one or more elements in a vector or matrix.

Solution

NumPy’s arrays make that easy

要求：访问特定的值

selectedExample.py

import numpy as np

# create row vector
vector = np.array([1, 2, 3, 4, 5, 6])

# create matrix
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])

# select the third element of vector
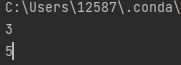
vector[2]
matrix[1,1]

结果：

Discussion

• numpy的数组下标从0开始

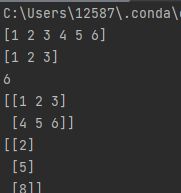
• With that caveat, NumPy offers a wide variety of methods for selecting (i.e., indexing and slicing) elements or groups of elements in arrays:（numpy数组提供了许多种访问方法）

  #访问全部元素
  vector[:]
  # 切片访问
  vector[:3]
  # 逆向访问
  vector[-1]
  # 访问前两行
  matrix[:2, :]
  # 访问所有行，第二列
  matrix[:,1:2]
  

结果：

1.5 Describing a Matrix

Problem

You want to describe the shape, size, and dimensions of the matrix

Solution

Use shape, size, and ndim:

描述矩阵信息

describeExample.py

# load library
import numpy as np

# create matrix
matrix = np.array([[1, 2, 3, 4],
                   [5, 6, 7, 8],
                   [9, 10, 11, 12]])

# 行和列
print(matrix.shape)
#大小
print(matrix.size)
#维度
print(matrix.ndim)

结果：

1.6 Applying Operations to Elements

Problem

You want to apply some function to multiple elements in an array.

Solutions

Use NumPy’s vectorize:

对多个元素进行函数操作

# load library
import numpy as np

# create matrix
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])

print(matrix)

#创建一个函数
add_1000 = lambda i: i + 1000


# vectorized
vectorized_add_1000 = np.vectorize(add_1000)

# 适用该函数
vectorized_add_1000(matrix)

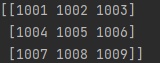
print(matrix)

运行结果

Discusion

NumPy’s vectorize class converts a function into a function that can apply to all elements in an array or slice of an array. It’s worth noting that vectorize is essentially a for loop over the elements and does not increase performance. Furthermore, NumPy arrays allow us to perform operations between arrays even if their dimensions are not the same (a process called broadcasting). For example, we can create a much simpler version of our solution using broadcasting:

• vectorized可应用于数组和数组切片的所有元素

• 本质上vectorized是for循环不会提升性能

• 另外即使维度不同数组之间也可以进行操作，例如广播

  matrix+1000
  

1.7 Finding Maximum and Minimum Values

Problem

You need to find the maximum or minimum value in an array.

Solution

Use NumPy’s max and min:

findingExample.py

# load library
import numpy as np

# create matrix
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])

# 最大值
np.max(matrix)
# 最小值
np.min(matrix)

结果：

Discussion

Often we want to know the maximum and minimum value in an array or subset of an array. This can be accomplished with the max and min methods. Using the axis parameter we can also apply the operation along a certain axis:

我们可以通过axis参数来求出每行或每列的最值

# 每行最值
print(np.max(matrix, axis=0))
# 每列最值
print(np.max(matrix, axis=1))

结果

1.8 Calculating the Average, Variance, and Standard Deviation

Problem

You want to calculate some descriptive statistics about an array.

Solution

Use NumPy’s mean, var, and std:

计算数组的统计数据

calculateExample.py

# load library
import numpy as np

# create matrix
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])

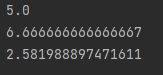
# mean是算术平均值
np.mean(matrix)
# var是 方差
np.var(matrix)
# deviation 是标准差
np.std(matrix)

结果

Discussion

Just like with max and min, we can easily get descriptive statistics about the whole matrix or do calculations alon a single axis:

也可以像min和max一样可以指定axis：

# find the mean value in each column
np.mean(matrix, axis=0)

结果：[4. 5. 6.]

1.9 Reshaping Arrays

Problem

You want to change the shape (number of rows and columns) of an array without changing the element values.

Solution

Use NumPy’s reshape:

更改数组形状

reshapeExample.py

# load library
import numpy as np

# create 4x3 matrix
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9],
                   [10, 11, 12]])

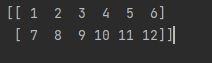
# 重构
matrix.reshape(2, 6)

结果：

Discussion

• The only requirement is that the shape of the original and new matrix contain the same number of elements (i.e., the same size). We can see the size of a matrix using size。reshape要求重构前和重构后的size相等，拥有相同数量

• reshape可以用参数-1表示尽可能多

• Finally, if we provide one integer, reshape will return a 1D array of that length:（如果只有一个数字那么数组将变为1维）

  print(matrix.size)
  print(matrix.reshape(1, -1))
  print(matrix.reshape(12))
  

  

1.10 Transposing a Vector or Matrix

Problem

You need to transpose a vector or matrix

Solution

Use the T method:

转置

transposingExample.py

# load library
import numpy as np

# create matrix
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])

# 转置矩阵
print(matrix.T)

结果

• Transposing is a common operation in linear algebra where the column and row indices of each element are swapped. One nuanced point that is typically overlooked outside of a linear algebra class is that, technically, a vector cannot be transposed because it is just a collection of values:（普通向量无法转置）

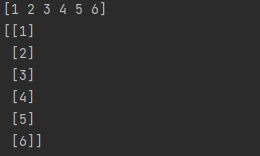
• However, it is common to refer to transposing a vector as converting a row vector to a column vector (notice the second pair of brackets) or vice versa:（行向量可以转置）

  # 转置向量
  np.array([1, 2, 3, 4, 5, 6]).T
  # 转置 行向量
  np.array([[1, 2, 3, 4, 5, 6]]).T
  

结果

1.11 Flattening a Matrix

Problem

You need to transform a matrix into a one-dimensional array.

Solution

Use flatten:

平铺矩阵,使用flatten()函数

# load library
import numpy as np

# create matrix
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])
# 平展矩阵
matrix.flatten()

输出：

Discussion

flatten is a simple method to transform a matrix into a one-dimensional array. Alternatively, we can use reshape to create a row vector:

#flatten等价于，但是不创建行向量
matrix.reshape(1, -1)

1.12 Finding the Rank of a Matrix

Problem

You need to know the rank of a matrix

Solution

Use NumPy’s linear algebra method matrix_rank:

计算矩阵的秩

rankExample

# load library
import numpy as np

# create matrix
matrix = np.array([[1, 1, 1],
                   [1, 1, 10],
                   [1, 1, 15]])

# 计算秩 
np.linalg.matrix_rank(matrix)

结果：2

Discussion

The rank of a matrix is the dimensions of the vector space spanned by its columns or rows. Finding the rank of a matrix is easy in NumPy thanks to matrix_rank.（求秩函数非常好用）

1.13 Calculating the Determinant

Problem

You need to know the determinant of a matrix

Solution

Use NumPy’s linear algebra method det:

求行列式

determinantExample.py

# load library
import numpy as np

# create matrix
matrix = np.array([[1, 2, 3],
                   [2, 4, 6],
                   [3, 8, 9]])

# 计算行列式
np.linalg.det(matrix)

结果：0.0

Discussion

It can sometimes be useful to calculate the determinant of a matrix. NumPy makes this easy with det

计算行列式非常好用

1.14 Getting the Diagonal of a Matrix

Problem

You need to get the diagonal elements of matrix.

Solution

Use diagonal:

矩阵的对角线用diagonal函数

diagonalExample.py

# load library
import numpy as np

# create matrix
matrix = np.array([[1, 2, 3],
                   [2, 4, 6],
                   [3, 8, 9]])

# 对角线
print(matrix.diagonal())

结果：

Discussion

NumPy makes getting the diagonal elements of a matrix easy with diagonal. It is also possible to get a diagonal off from the main diagonal by using the offset parameter:

可以用offset函数获得副对角线

print(matrix.diagonal(offset=1))
print(matrix.diagonal(offset=-1))

1.15 Calculating the Trace of a Matrix

Problem

You need to calculate the trace of a matrix

Solution

Use trace:

计算矩阵的迹

traceExample.py

# load library
import numpy as np

# create matrix
matrix = np.array([[1, 2, 3],
                   [2, 4, 6],
                   [3, 8, 9]])

# 矩阵的迹
matrix.trace()

结果：1+4+9=14

Discussion

The trace of a matrix is the sum of the diagonal elements and is often used under the hood in machine learning methods. Given a NumPy multidimensional array, we can calculate the trace using trace. We can also return the diagonal of a matrix and calculate its sum:

• 矩阵的迹通常在底层适用
• 多维数组我们可以通过trace计算轨迹
• 等价于sum函数求对角线和

#等价
print(sum(matrix.diagonal()))

1.16 Finding Eigenvalues and Eigenvectors

Problem

You need to find the eigenvalues and eigenvectors of a square matrix.

Solution

Use NumPy’s linalg.eig:

特征值和特征向量

eigenExample.py

# load library
import numpy as np

# create matrix
matrix = np.array([[1, -1, 3],
                   [1, 1, 6],
                   [3, 8, 9]])

#计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(matrix)

# 特征值
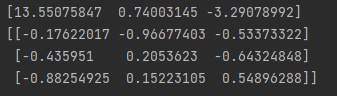
print(eigenvalues)
# 特征向量
print(eigenvectors)

Discussion

Eigenvectors are widely used in machine learning libraries. Intuitively, given a linear transformation represented by a matrix, $A$, eigenvectors are vectors that, when that transformation is applied, change only in scale (not direction). More formally:

$$Av=\lambda v$$

where $A$ is a square matrix, $\lambda$ contains the eigenvalues and $v$ contains the eigenvectors. In NumPy’s linear algebra toolset, eiglets us calculate the eigenvalues, and eigenvectors of any square matrix.

(解释特征值$\lambda$和特征向量$v$的定义)

1.17 Calculating Dot Products

Problem

You need to calculate the dot product of two vectors.

Solution

Use NumPy’s dot:

向量点积

dotExample

# load library
import numpy as np

# create two vectors
vector_a = np.array([1, 2, 3])
vector_b = np.array([4, 5, 6])

# 计算点积
print(np.dot(vector_a, vector_b))
print(vector_a@vector_b)

结果

Discussion

• The dot product of two vectors, a and b, is defined as:（点积定义）

  $$\sum (a_i\ast b_i)$$

• where $a_i$ is the ith element of vector a. We can use NumPy’s dot class to calculate the dot product. Alternatively, in Python 3.5+ we can use the new @operator:（3.5版本以上可以用@）

  vector_a @ vector_b
  

1.18 Adding and Subtracting Matricies

Problem

You want to add or subtract two matricies

Solution

Use NumPy’s add and subtract:

Discussion

Alternatively, we can simply use the + and - operators:

加法和减法

addAndSubstract.py

# load library
import numpy as np

# create matricies
matrix_a = np.array([[1, 1, 1],
                     [1, 1, 1],
                     [1, 1, 2]])

matrix_b = np.array([[1, 3, 1],
                     [1, 3, 1],
                     [1, 3, 8]])

# +
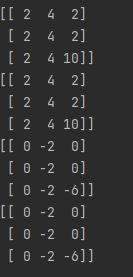
print(np.add(matrix_a, matrix_b))
# +
print(matrix_a + matrix_b)
# -
print(np.subtract(matrix_a, matrix_b))
# -
print(matrix_a - matrix_b)

1.19 Multiplying Matricies

Problem

You want to multiply two matrices.

Solution

Use NumPy’s dot:

Discussion

Alternatively, in Python 3.5+ we can use the @ operator:

矩阵点乘

# load library
import numpy as np

# create matrices
matrix_a = np.array([[1, 1],
                     [1, 2]])

matrix_b = np.array([[1, 3],
                     [1, 2]])

# multiply two matrices
np.dot(matrix_a, matrix_b)

1.20 Inverting a Matrix

Problem

You want to calculate the inverse of a square matrix.

Solution

Use NumPy’s linear algebra inv method:

invertingExample.py

# load library
import numpy as np

# create matrix
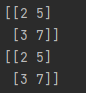
matrix = np.array([[1, 4],
                  [2, 5]])

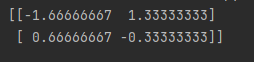
# inv求逆
print(np.linalg.inv(matrix))

Discussion

The inverse of a square matrix, $A$, is a second matrix $A^{–1}$, such that:

$A\ast A^{-1}=I$

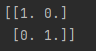
where $I$ is the identity matrix. In NumPy we can use linalg.inv to calculate $A^{–1}$ if it exists. To see this in action, we can multiply a matrix by its inverse and the result is the identity matrix:

（定义：矩阵乘其逆矩阵得到单位矩阵）

print(matrix @ np.linalg.inv(matrix))

1.21 Generating Random Values

Problem

You want to generate pseudorandom values.

Solution

Use NumPy’s random:

生成随机值

randomExample.py

# load library
import numpy as np

# 设置种子
np.random.seed(0)

# 生成大小为3的随机数组
print(np.random.random(3))

Discussion

• NumPy offers a wide variety of means to generate random numbers, many more than can be covered here. In our solution we generated floats; however, it is also common to generate integers:

  (numpy提供了许多生成随机数的方法，可以生成整数)

• Alternatively, we can generate numbers by drawing them from a distribution:

  （我们可以从特殊分布中提取数字）

• Finally, it can sometimes be useful to return the same random numbers multiple times to get predictable, repeatable results. We can do this by setting the “seed” (an integer) of the pseudorandom generator. Random processes with the same seed will always produce the same output. We will use seeds throughout this book so that the code you see in the book and the code you run on your computer produces the same results.

（有时可以通过设置相同的种子来产生多次相同的值，这有时候会很有用；种子产生的是伪随机数）

# 生成3个在 1 和 10的随机整数
print(np.random.randint(0, 11, 3))
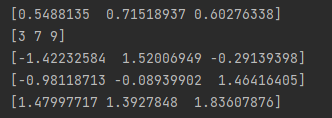
# 从均值为0的正态分布生成三个随机数
# 方差为1
print(np.random.normal(0.0, 1.0, 3))
# 从logistic分布中获得3个随机数
print(np.random.logistic(0.0, 1.0, 3))
# 从均值分布中获得3个随机数
print(np.random.uniform(1.0, 2.0, 3))

下一章：(88条消息) Machine Learning with Python Cookbook 学习笔记 第2章_五舍橘橘的博客-CSDN博客