Machine Learning with Python Cookbook 学习笔记 第9章

Chapter 9. Dimensionality Reduction Using Feature Extraction

前言

• 本笔记是针对人工智能典型算法的课程中Machine Learning with Python Cookbook的学习笔记
• 学习的实战代码都放在代码压缩包中
• 实战代码的运行环境是python3.9 numpy 1.23.1 anaconda 4.12.0
• 上一章：(97条消息) Machine Learning with Python Cookbook 学习笔记 第8章_五舍橘橘的博客-CSDN博客
• 代码仓库
  • Github:yy6768/Machine-Learning-with-Python-Cookbook-notebook: 人工智能典型算法笔记 (github.com)
  • Gitee:yyorange/机器学习笔记代码仓库 (gitee.com)

9.0 Introduction

• 访问数十万的feature是很常见的。
• 幸运的是，并非所有特征都是平等的，降维特征提取的目标是转换我们的特征集 poriginal ，以便我们最终得到一个新的集合 pnew ，其中 poriginal > pnew ，同时仍然保留大部分基础信息。换句话说，我们减少了特征的数量，而我们的数据生成高质量的能力只有很小的损失 预测。
• 在本章中，我们将介绍一些特征提取技术来做到这一点。 我们讨论的特征提取技术的一个缺点是我们生成的新特征将无法被人类解释。它们将包含与训练我们的模型一样多或几乎一样多的能力，但在人眼中将显示为随机数的集合。如果我们想保持解释模型的能力，通过特征选择降维是更好的选择。

9.1 Reducing Features Using Principal Components

• 使特征降维，但是保持数据中的方差
• scikit’s PCA

PCA.py

# Load libraries
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn import datasets
# 加载数据
digits = datasets.load_digits()
# 是数据集标准化
features = StandardScaler().fit_transform(digits.data)
# 创建一个保留99%方差的PCA
pca = PCA(n_components=0.99, whiten=True)
# 生成一个PCA features
features_pca = pca.fit_transform(features)
# 显示
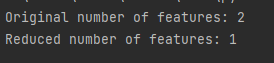
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_pca.shape[1])

Discussion

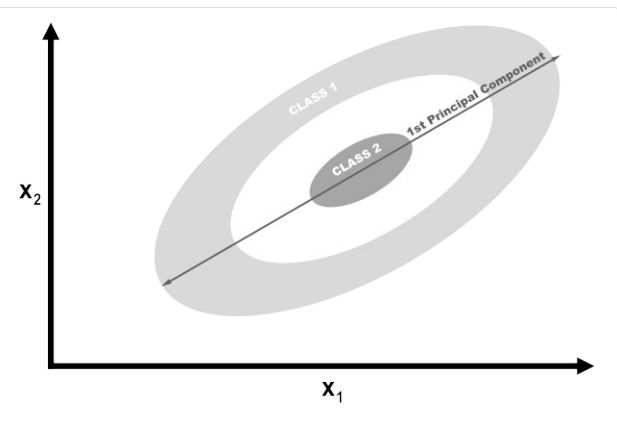
• Principal component analysis (PCA) 是一种流行的降维技术
• PCA 将观察结果投射到特征矩阵中保留最大方差的（希望更少）主成分上。
• PCA 是一种无监督技术，这意味着它不使用来自目标向量的信息，而只考虑特征矩阵。
• PCA 是在 scikit-learn 中使用 pca 方法实现的。
  • n_components 有两个操作，具体取决于提供的参数。如果n_components大于 1，它将返回参数所指定数量的特征，这导致了如何选择最优特征数量的问题。对我们来说，如果 n_components 的参数介于 0 和 1 之间，pca 会返回保留方差的最小特征量。我们通常使用 0.95 和 0.99 的值，这意味着分别保留了原始特征的 95% 和 99% 的方差。
  • whiten=True 转换每个主成分的值，使它们具有零均值和单位方差。（标准化）
  • 还有一个参数是svd_solver=“randomized”，它实现了一种随机算法，通常会以更短的时间找到第一个主成分。

PCA的数学原理

• 原书并没有介绍非常详细，只是简单举了一个例子

• 在这里看了几篇资料比较详细的是【机器学习】降维——PCA（非常详细） - 知乎 (zhihu.com)

• 概述：PCA（Principal Component Analysis） 是一种常见的数据分析方式，常用于高维数据的降维，可用于提取数据的主要特征分量。

• 原理：

  • 首先我们在数学上学过基的概念，如果想要把一个N维向量投影到k维，需要选择K个基，那么如何选择K个基使这N个向量保留原有的信息就是我们需要解决的问题；

  • 我们也学过方差（协方差），方差在一维上表示数值的分散程度，那么我们上述的问题其实也就简化成了所有数据变换转换到对应的基上，数据在这个基的方差最大

  • 为了方便计算我们需要对数据进行标准化（也就对应了案例中执行features = StandardScaler().fit_transform(digits.data)的语句）

  • 

  • 那么最后我们的问题就化简成了：将一组 N 维向量降为 K 维，其目标是选择 K 个单位正交基，使得原始数据变换到这组基上后，各变量两两间协方差为 0，而变量方差则尽可能大（在正交的约束下，取最大的 K 个方差）。

  • 根据我们的优化条件，我们需要将除对角线外的其它元素化为 0，并且在对角线上将元素按大小从上到下排列（变量方差尽可能大）

  • 矩阵对角化：原数据协方差矩阵C和转换后的协方差矩阵D满足：

    • $$\begin{gathered} D=\frac{1}{m}Y{Y}^T \\ =\frac{1}{m}(PX)(PX{)}^T \\ =\frac{1}{m}PX{X}^T{P}^T \\ =P(\frac{1}{m}X{X}^T)P^T=PC{P}^T \end{gathered}$$

    • （P是一组基，X是原来的矩阵，Y是转换后的矩阵,D是转换后的协方差矩阵，C是转换前的协方差矩阵）

    • 可以看得出我们实际上就是需要将C进行对角化处理=>目标：寻找一个矩阵 P，满足 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-P9KFuihY-1658540787278)(https://www.zhihu.com/equation?tex=PCP%5ET)] 是一个对角矩阵，并且对角元素按从大到小依次排列，那么 P 的前 K 行就是要寻找的基，用 P 的前 K 行组成的矩阵乘以 X 就使得 X 从 N 维降到了 K 维并满足上述优化条件。

  • 协方差矩阵有这样的特性：

    • 是一个实对称矩阵：实对称矩阵不同特征值对应的特征向量必然正交。
    • 设特征向量 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8PYizB6K-1658540787278)(https://www.zhihu.com/equation?tex=%5Clambda)] 重数为 r，则必然存在 r 个线性无关的特征向量对应于 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ineBXQgd-1658540787279)(https://www.zhihu.com/equation?tex=%5Clambda)] ，因此可以将这 r 个特征向量单位正交化。

    所以可以得出结论：协方差矩阵一定可以找到N个线性无关的单位正交向量，我们可以按列组成矩阵

    $E=(e_1,e_2,.....,e_N)$

    结合1、2两点可以得到：$E^{T}CE=\Lambda$

    其中$\Lambda$是对角矩阵，所以其实就可以得出$P=E^T$

  • 所以根据前面的优化条件我们已经可以得出我们所需的矩阵P，P是协方差矩阵特征向量单位化后按照从大到小的顺序排列出来的矩阵，其中每一行都是原矩阵C的特征向量，根据需要的维数将P压缩成P‘（前K行）$Y=P^{\prime }X$得到降维后的Y

  • 总结就是6步：

    • 将原始数据按列组成 n 行 m 列矩阵 X；
    • 将 X 的每一行进行零均值化，即减去这一行的均值；（标准化）
    • 求出协方差矩阵 $C=\frac{1}{m}X{X}^T$ ；
    • 求出协方差矩阵的特征值及对应的特征向量；
    • 将特征向量按对应特征值大小从上到下按行排列成矩阵，取前 k 行组成矩阵 P；
    • $Y=PX$ 即为降维到 k 维后的数据。

9.2 Reducing Features When Data Is Linearly Inseparable（线性不可分）

• 线性可分就是说可以用一个线性函数把两类样本分开
• 目标是把线性可分的数据进行降维
• 使用拓展的PCA算法——Kernel PCA 对非线性数据进行降维

linearlyInseparable.py

# Load libraries
from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import make_circles
# 创建一个线性可分的数据 圆数据集
features, _ = make_circles(n_samples=1000, random_state=1, noise=0.1, factor=0.1)
# 使用 kernal PCA  核函数RBF（高斯核函数） 系数15，降维到1维
kpca = KernelPCA(kernel="rbf", gamma=15, n_components=1)
features_kpca = kpca.fit_transform(features)
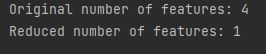
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_kpca.shape[1])

Discussion

• PCA用于降维。标准PCA用于线性情况的降维，如果是线性可分的数据集（可以用直线或者超平面将类分开）那么PCA的降维效果很好，反之，PCA降维效果就不行

• make_circles产生同心圆的数据集，这两个圆是线性可分的

  

• 但在本问题中，如果我们像上一节一样使用线性的PCA那么因为两个圆是非线性的，他们的投影会交织在一起，效果很差

• 理想情况下，我们需要一个既可以减少维度又可以使数据线性可分的转换。而KernelPCA就可以同时做到两个目标

• 内核允许我们将线性不可分的数据投影到线性可分的更高维度； 这称为kernel trick

• Kernel（这里应该指的是核函数）允许我们将线性不可分的数据投影到线性可分的更高维度。

• KernelPCA可以允许提供很多内核包括poly(多项式)，gbf(高斯核)，sigmoid（sigmoid函数），甚至linear(线性函数）

• linear情况下的效果与线性PCA一模一样

• KernelPCA一个缺点就是需要我们指定很多参数n_components表示参数数量，核函数本身就需要参数，例如本例中gbf核就需要gamma值

• 我们将在12章讨论如何确定这些参数

KernelPCA的原理

数据降维: 核主成分分析(Kernel PCA)原理解析 - 知乎 (zhihu.com)

• 大致复述一下详细的原理：

  • 对比PCA，我们需要将特征矩阵映射到更高维的空间，所以需要定义一个函数$\varphi (x):R^K\to R^D$ (这里D远大于K，意在于把特征向量映射到更高维的空间，使他可以被线性超平面划分)，所以对于整个特征矩阵都可以得到$\varphi (X)=[\varphi (x_1),\varphi (x_2),\dots \dots \varphi (x_n)]$

  • 之后就类似于PCA,我们先对原来的数据去中心化后，可以得到协方差矩阵$C_f=\frac{1}{n}\varphi (X)\varphi (X{)}^T$

  • 然后就转换成协方差矩阵的对角化问题：$p^T\frac{1}{n}\phi (X)\phi (X)^Tp=\Lambda $

  • 但是我们没有办法求出$\varphi (X)$，所以没有办法直接计算

  • kernel trick:因为我们只需要求较大的特征向量，所以我们并不需要求出实际的$\varphi (X)$

    • 因为我们已经得到$$p^T\frac{1}{N}\varphi (X)\varphi (X{)}^{T}p=\Lambda$$=>$\lambda p={\Sigma }_{i=1}^n\varphi (x_i)\varphi (x_i{)}^{T}p（1）$

    • 两边除以$\lambda$,得到$p=\frac{1}{\lambda }{\Sigma }_{i=1}^n\varphi (x_i)[\varphi (x_i{)}^{T}p]$

    • 使用方括号标出的部分为标量，上式表明，如果$\lambda \ne 0$，特征向量可以表示成$\varphi (x_i)$的一个线性组合：

      $p={\Sigma }_{i=1}^n{\alpha }_i\varphi (x_i)=\varphi (X)\alpha (2)$

      其中$\alpha =[{\alpha }_1,{\alpha }_2...,{\alpha }_n{]}^T$

    • 之后只需要把（2）式代入（1）：

      得到$\varphi (X{)}^T\varphi (X)\varphi (X{)}^T\varphi (X)\alpha =\varphi (X{)}^T\varphi (X)\alpha$

      定义$K=\varphi (X{)}^T\varphi (X)$

      所以只需求$K\alpha =\lambda \alpha$即可

    • 之后我们注意到K是一个对称矩阵，所以求出来的特征值对应着（1）式的特征值

    • 现在的问题就是如何计算K

    • 核技巧就是不需要声明$\varphi$只需要使用常用的核函数$k(x,y)=\varphi (x{)}^T\varphi (y)$,通过核函数，我们可以直接使用两个低维度向量x，y得到他们在高维的点积，所以我们就可以通过$k(x_i,x_j)$计算K矩阵，最后计算出$\alpha$

• 需要注意的点有：

  • 协方差矩阵和对角化的大部分与之前PCA的一致，大多数不同点集中在如何通过线性组合和线性变换使得我们把问题转换到另一个求特征向量的问题

  • 非线性映射 $\varphi$ 将 $X$ 中的向量 $x$，但是这个$\varphi$是不会显示指定的，只需要定义出高维特征空间的空间向量即可，这就是kernel trick的本质

  • 和PCA一样，为了方便协方差矩阵的计算，我们需要将数据进行去中心化处理

9.3 Reducing Features by Maximizing Class Separability

• 通过分类器来减少特征
• linear discriminant analysis (LDA)

# Load libraries
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 莺尾花数据
iris = datasets.load_iris()
features = iris.data
target = iris.target
# 创建lda
lda = LinearDiscriminantAnalysis(n_components=1)
features_lda = lda.fit(features, target).transform(features)
# 打印
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_lda.shape[1])
# 方差
print(lda.explained_variance_ratio_)

Discussion

• LDA 是一种分类方法，也是一种流行的降维技术。
• 对比LDA的不同：
  • LDA算法的思想是将数据投影到低维空间之后，使得同一类数据尽可能的紧凑，不同类的数据尽可能分散。
  • LDA是有监督的机器学习算法
  • LDA根据的是均值，PCA根据的是方差
• 在 scikit-learn 中，LDA 是使用 LinearDiscriminantAnalysis 实现的， 其中包括一个参数 n_components，表示我们想要返回的特征数量。
• 具体来说，我们可以运行 LinearDiscriminantAnalysis 并将 n_components 设置为 None 以返回每个组件特征解释的方差比率，然后计算需要多少组件才能超过某个解释的方差阈值（通常为 0.95 或 0.99）

​ 官方文档表明：If None, will be set to min(n_classes - 1, n_features)

# 测试参数
lda = LinearDiscriminantAnalysis(n_components=None)
features_lda = lda.fit(features, target)
# 方差值
lda_var_ratios = lda.explained_variance_ratio_
print(lda_var_ratios)


# 计算n_components多大时才能够达到goal_var的阈值
def select_n_components(var_ratio, goal_var: float) -> int:
    # 设置初始的参数
    total_variance = 0.0
    # 初始的特征数
    n_components = 0
    # 对于每个ratio计算
    for explained_variance in var_ratio:
        # Add the explained variance to the total
        total_variance += explained_variance
        # Add one to the number of components
        n_components += 1
        # If we reach our goal level of explained variance
        if total_variance >= goal_var:
            # End the loop
            break
    # Return the number of components
    return n_components


# 运行函数
print(select_n_components(lda_var_ratios, 0.99))

LDA原理

机器学习-LDA(线性判别降维算法) - 知乎 (zhihu.com)

机器学习-降维方法-有监督学习：LDA算法(线性判别分析)【流程：①类内散度矩阵Sw-＞②类间散度矩阵Sb-＞计算Sw^-1Sb的特征值、特征向量W-＞得到投影矩阵W-＞将样本X通过W投影进行降维】_u013250861的博客-CSDN博客_有监督lda

1. 首先明确目的：我们需要在降维后保持特征不重合的同时还要保证类内数据紧凑，类之间数据分散；

2. 我们需要把数据投影到一个超平面上（两类的就是直线上），那么现在就需要考虑如何确定这个超平面来保证类间和类内的点的距离

3. 假设就是2个类，投影在一条直线上，那么我们必须要保证类之间的距离最大，那么可以通过类中心来计算：假设${\mu }_1是第一个类的中心，{\mu }_2是第二个类的中心$，那么距离计算就是

   $|w^T{\mu }_1-w^T\mu 2|$($w^T$是投影方向转置)

4. 同时要类内距离最短，我们就需要类内的差距最小，那么自然而然就想到的是方差的计算方式，不过在这里定义的不是协方差矩阵而是散度矩阵（链接2其实介绍了两者本质无区别只是差了个常数）

​ ${\Sigma }_j(j=1,2)={\Sigma }_{x\in X_j}(x-{\mu }_j)(x-{\mu }_j{)}^T$

​ 那么需要最小化$w^T{\Sigma }_{0}w+w^T{\Sigma }_{1}w$

5、我们定义类内散度矩阵为：$S_w={\Sigma }_0+{\Sigma }_1$,类间散度矩阵为$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$

6、最后我们得到目标$argmaxJ(w)=w^T{S}_{b}w/w^T{S}_{w}w$

7、求J对W的偏导数取0，此时J最大，化简等式得到：$(w^T{S}_{B}w)S_{w}w=(w^T{S}_{w}w)S_{B}w$

8、由于（7）式内用括号括起来的都只是一个值，我们定义$\lambda =w^T{S}_{B}w/w^T{S}_{w}w$

9、根据（7）（8）化简得到$S_w^{-1}{S}_{B}w=\lambda w$最后只需要按照特征向量的求法，求出$w$即可得到我们需要的投影方向

9.4 Reducing Features Using Matrix

• 对一个没有负值的矩阵进行降维
• NMF算法

NMF.py

# Load libraries
from sklearn.decomposition import NMF
from sklearn import datasets
# 加载data
digits = datasets.load_digits()
# 加载特征矩阵
features = digits.data
# 创建、转换和应用 NMF
nmf = NMF(n_components=10, random_state=1)
features_nmf = nmf.fit_transform(features)
# 展示结郭
print("Original number of features:", features.shape[1])
print("Reduced number of features:", features_nmf.shape[1])

Discussion

• non-negative matrix factorization (NMF) 是一种用于线性降维的无监督技术，它将特征矩阵分解（即分解为乘积近似于原始矩阵的多个矩阵）为表示观察值与其特征之间潜在关系的矩阵。
• $V=WH$ 形式上，给定需要返回的特征 r，NMF 将我们的特征矩阵分解为： 其中 V 是我们的 d × n 特征矩阵（即 d 个特征，n 个观察值），W 是一个 d × r，H 是一个 r × n 矩阵。通过调整 r 的值，我们可以设置所需的降维量。
• NMF 没有为我们提供输出特征的解释方差。因此，我们找到 n_components 最佳值的最佳方法是尝试一系列值，以找到在最终模型中产生最佳结果的值（参见第 12 章）。

NMF原理

• 实际上上网搜索发现原书已经将基本的NMF原理讲出来了，所以没有什么其他的
• 但是对于更详细的信息网上可以参考这篇博客：NMF 非负矩阵分解 – 原理与应用_qq_26225295的博客-CSDN博客_nmf原理
• 其实大部分NMF的问题不是原理问题，而是K值，也就是这个n_components的参数怎么定才合适

9.5 Reducing Features on Sparse Data

• 对稀疏矩阵降维
• TSVD

TSVD.py

# Load libraries
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import TruncatedSVD
from scipy.sparse import csr_matrix
from sklearn import datasets
import numpy as np
# Load the data
digits = datasets.load_digits()
# 标准化
features = StandardScaler().fit_transform(digits.data)
# 稀疏化
features_sparse = csr_matrix(features)
# 创建一个 TSVD
tsvd = TruncatedSVD(n_components=10)
# 应用 TSVD
features_sparse_tsvd = tsvd.fit(features_sparse).transform(features_sparse)
# 显示
print("Original number of features:", features_sparse.shape[1])
print("Reduced number of features:", features_sparse_tsvd.shape[1])

Discussion

• Truncated Singular Value Decomposition(TSVD) 截断奇异值分解

• TSVD 类似于 PCA，事实上，PCA 实际上经常在其步骤之一中使用非截断奇异值分解 (SVD)。TSVD 的实际优势在于，与 PCA 不同，它适用于稀疏特征矩阵。

• TSVD 的一个问题是，由于它使用随机数生成器的方式，输出的符号可以在拟合之间翻转。一个简单的解决方法是每个预处理管道只使用一次 fit，然后多次使用 transform。

• 与LDA一样，我们必须指定我们想要输出的特征（components）的数量。这是通过 n_components 参数完成的。

• 那么一个自然而然的问题就是：components的最佳数量是多少？

  • 一种策略是将 n_components 作为hyperparameter包含在模型选择期间进行优化（即，选择 n_components 的值以产生最佳训练模型）
  • 由于 TSVD 为我们提供了每个分量解释的原始特征矩阵方差的比率，我们可以选择解释所需方差量的分量的数量（95% 或 99% 是常用值）。

  # 打印前3个维度上的方差和
  print(tsvd.explained_variance_ratio_[0:3].sum())
  

  

# 创建一个tsvd并运用
tsvd = TruncatedSVD(n_components=features_sparse.shape[1] - 1)
features_tsvd = tsvd.fit(features)
# 列出所有方差
tsvd_var_ratios = tsvd.explained_variance_ratio_


# 创建类似于第二节的function
def select_n_components(var_ratio, goal_var):
    total_variance = 0.0
    n_components = 0
    # 对于每一个比例的方差来说:
    for explained_variance in var_ratio:
        total_variance += explained_variance
        n_components += 1
        # 一旦方差大于指定的方差，返回
        if total_variance >= goal_var:
            break
    # Return the number of components
    return n_components


# 计算components
print(select_n_components(tsvd_var_ratios, 0.95))

TSVD原理

• 【zt】TSVD - 简书 (jianshu.com)

• TSVD截断奇异值分解_像在吹的博客-CSDN博客_截断奇异值分解

• 网上的TSVD讲的比较少，因为TSVD是SVD的变形，所以大多都是讲SVD

• TruncatedSVD与SVD最大的不同是只计算用户指定的最大的K个奇异值（特征值）

• TSVD实际上算法和PCA特别像实际上就是把协方差矩阵变成矩阵本身，所以过程上本质也是求出对角化矩阵并按照特征值按顺序大小进行排列的操作

下一章：(97条消息) Machine Learning with Python Cookbook 学习笔记 第10章_五舍橘橘的博客-CSDN博客