线性回归的简单python实现
单变量简单线性回归
以波士顿房价问题为例,数据集中共有三个输入变量,一个输出变量,在此我们只是用其中一个输入变量来进行拟合。
1、首先读取数据文件,python中的pandas库可以处理多种格式的数据文件,以csv文件为例,将数据集数据读入内存中:
# 读取数据文件
data=pd.read_csv("housing.csv")
examdf=DataFrame(data)2、将整个数据集划分为训练集和测试集,在这里用到了sklearn库中的train_test_split函数,该函数用于数据集的划分,设置训练集占80%,然后输出他们的样本量:
X_train,X_test,Y_train,Y_test = train_test_split(examdf.RM,examdf.MEDV,train_size=0.8)
print("自变量---源数据:",examdf.RM.shape, "; 训练集:",X_train.shape, "; 测试集:",X_test.shape)
print("因变量---源数据:",examdf.MEDV.shape, "; 训练集:",Y_train.shape, "; 测试集:",Y_test.shape)输出为:
可以看出,数据集中共有489的数据,其中391个被划分为训练集,98个被划分为测试集。
3、建立线性回归模型并使用训练集进行训练,由于此时X_train和Y_train都是一维数组,需要把他们转化为二维矩阵才可以,在这里借助numpy库中的reshape函数,将其转化为二维矩阵。
# 初始化训练模型
model=LinearRegression()
# 线性回归训练
X_train_new=np.array(X_train).reshape(-1,1)
Y_train_new=np.array(Y_train).reshape(-1,1)
model.fit(X_train_new,Y_train_new)4、使用测试集数据进行测试,得到预测结果,并将预测结果与真实结果绘制折线图,可以直观的表现出拟合效果。
X_test_new=np.array(X_test).reshape(-1,1)
y_test_predict=model.predict(X_test_new)
plt.plot(range(len(y_test_predict)),y_test_predict,'red', linewidth=2.5,label="predict data")
plt.plot(range(len(Y_test)),Y_test,'green',label="test data")
plt.legend(loc=2)
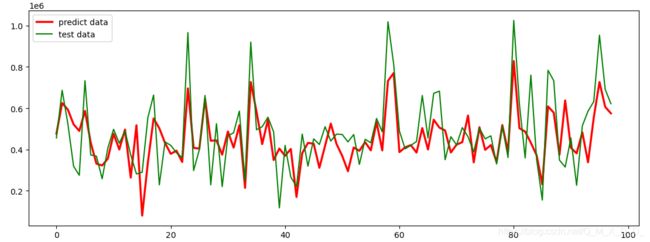
plt.show()输出结果如下图所示,其中绿色的是真实结果,红色的是程序预测结果:
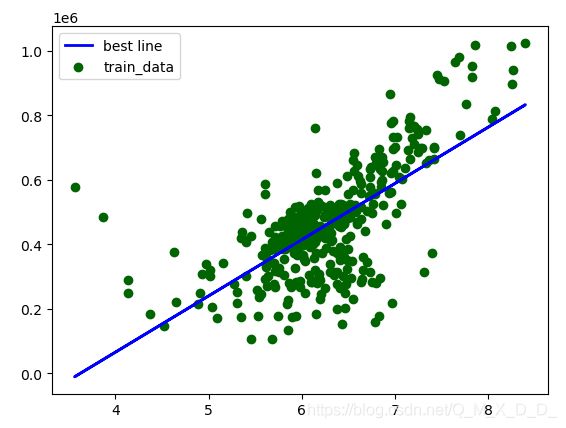
5、我们还可以将拟合函数与测试集数据画出来,也可以直观的看到回归函数与训练集的贴合程度。模型是使用训练集数据拟合出来的函数来进行预测的,所以将训练集数据输入到模型中就可以得到拟合函数。
y_train_predict=model.predict(X_train_new)
plt.plot(X_train,y_train_predict,color="blue",linewidth=2,label="best line")
plt.scatter(X_train,Y_train,color="darkgreen",label="train_data")
plt.legend(loc=2)
plt.show()输出结果为:
多变量线性回归
使用三个输入变量时就是多变量线性回归。
1、首先仍然是要读取数据集中的数据
data=pd.read_csv("housing.csv")
examdf=DataFrame(data)2、将数据集拆分为训练集和测试集,并创建回归模型,将训练集数据输入其中进行拟合。由于此时输入变量有三个,训练集就是一个二维数组,不需要用到reshape函数。
X_train,X_test,Y_train,Y_test = train_test_split(examdf.loc[:,:"PTRATIO"],examdf.MEDV,train_size=0.8)
model=LinearRegression()
model.fit(X_train,Y_train)3、使用测试集数据进行测试,并与真实结果进行对比。
Y_pred = model.predict(X_test)
plt.plot(range(len(Y_pred)),Y_pred,'red', linewidth=2.5,label="predict data")
plt.plot(range(len(Y_test)),Y_test,'green',label="test data")
plt.legend(loc=2)
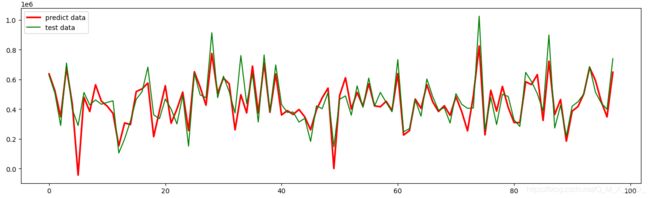
plt.show()输出结果如下图所示,可以看出比单变量的拟合效果更好一些: