基于MATLAB的K-means聚类算法
实验数据说明
Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性预测鸢尾花卉属于（Setosa(山鸢尾)，Versicolour(杂色鸢尾)，Virginica(维吉尼亚鸢尾)）三个种类中的哪一类。
鸢尾花（iris）数据集，它共有4个属性列和一个品种类别列：sepal length（萼片长度）、sepal width（萼片宽度）、petal length（花瓣长度）、petal width （花瓣宽度），单位都是厘米。3个品种类别是Setosa、Versicolour、Virginica，样本数量150个，每类50个。
技术介绍
聚类：一个将数据集中在某些方面相似的数据成员进行分类组织的过程.
K-means聚类：属于无监督学习的方法，K表示类别数，Means表示均值，K一般由人工来指定，或通过层次聚类(Hierarchical Clustering)的方法获得数据的类别数量作为选择K值的参考
选择较大的K可以降低数据的误差，但会增加过拟合的风险。
算法过程：
（1）随机选取K个初始质心
（2）分别计算所有样本到这K个质心的距离
（3）如果样本离质心Si最近，那么这个样本属于Si点群；如果到多个质心的距离相等，则可划分到任意组中
（4）按距离对所有样本分完组之后，计算每个组的均值（最简单的方法就是求样本每个维度的平均值），作为新的质心
（5）重复（2）（3）（4）直到新的质心和原质心相等，算法结束
考虑欧几里得距离的数据，使用误差平方和（Sum of the Squared Error,SSE）作为聚类的目标函数，两次运行K均值产生的两个不同的簇集，我们更喜欢SSE最小的那个：
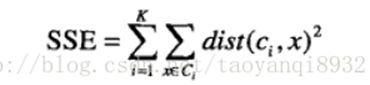
其中：k表示k个聚类中心，ci表示第几个中心，dist表示的是欧几里得距离。
前面说的我们更新质心是让所有的点的平均值，这里就是SSE所决定的：
实验一
**
用k-means聚类完成三维高斯分布数据的分类，以及结果可视化。
**
Step1:获取初始数据集：设置不同均值和协方差产生随机的高斯分布数据
mu1=[0 0 0]; %均值
S1=[0.3 0 0;0 0.35 0;0 0 0.3]; %协方差
data1=mvnrnd(mu1,S1,100); %产生高斯分布数据
Step2:将三类数据画在一个三维坐标
plot3(data1(:,1),data1(:,2),data1(:,3),'b+');
hold on;
plot3(data2(:,1),data2(:,2),data2(:,3),'r+');
plot3(data3(:,1),data3(:,2),data3(:,3),'g+');
grid on;
Step3:调用k-means进行聚类，其中参数含义如下
%ldx：每一类数据的分类标签
%data：输入的不带分类标号的数据
%c:每一个聚类中心的位置
%d:类间所有点与该类质心点距离之和
%re：最后产生带标号的数据，标号在所有数据的最后，意思就是数据再加一维度
[ldx,c,d]=kmeans2(data,3);
re=[data ldx];
Step4:画出聚类后的数据的三维坐标
Step5:画出聚类中每一个聚类中心的位置
plot3(c(1,1),c(1,2),c(1,3),'bo');
hold on;
plot3(c(2,1),c(2,2),c(2,3),'ro');
plot3(c(3,1),c(3,2),c(3,3),'go');
grid on;
预期图：
未聚类前的图
聚类后的图，黑色圆点代表聚类中心
实验二
**
使用k-means聚类实现鸢尾花数据的分类；
**
Step1:获取初始数据集
%Iris-setosa--0
%Iris-versicolor--1
%Iris-virginica--2
data=importdata('iris.csv');
Step2:将鸢尾花四维属性降二维
[data, mapping] = lda(data(:,1:4), data(:,5), 2);
Step3:调用k-means进行聚类，其中参数含义如下
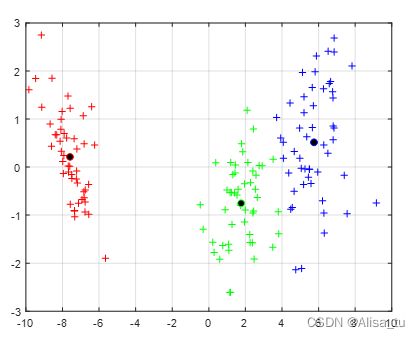
Step4:画出聚类后的数据的分布图
Step5:画出聚类中每一个聚类中心的位置
plot(c(1,1),c(1,2),'bo','MarkerFaceColor','black');
hold on;
plot(c(2,1),c(2,2),'ro','MarkerFaceColor','black');
plot(c(3,1),c(3,2),'go','MarkerFaceColor','black');
grid on;
效果图：下图为聚类后的分类图像，黑色圆点代表效果图
完整代码下载地址：
https://github.com/tutu424/matlab.git
