matlab编程实现k_means聚类（k均值聚类）

1. 聚类的定义

以下内容摘抄自周志华《机器学习》

根据训练数据是否拥有标记信息，机器学习任务可以大致分为两大类：“监督学习”（supervised learning）和“无监督学习”（unsupervised learning）。分类和回归是监督学习的代表，而聚类则是无监督学习的代表。
聚类试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个“簇”（cluster），通过这样的划分，每个簇可能对应一些潜在的概念（类别），而这些类别概念相对于聚类算法而言，事先是未知的，聚类过程只能自动形成簇结构，簇所对应的概念语义需由使用者来把握和命名。

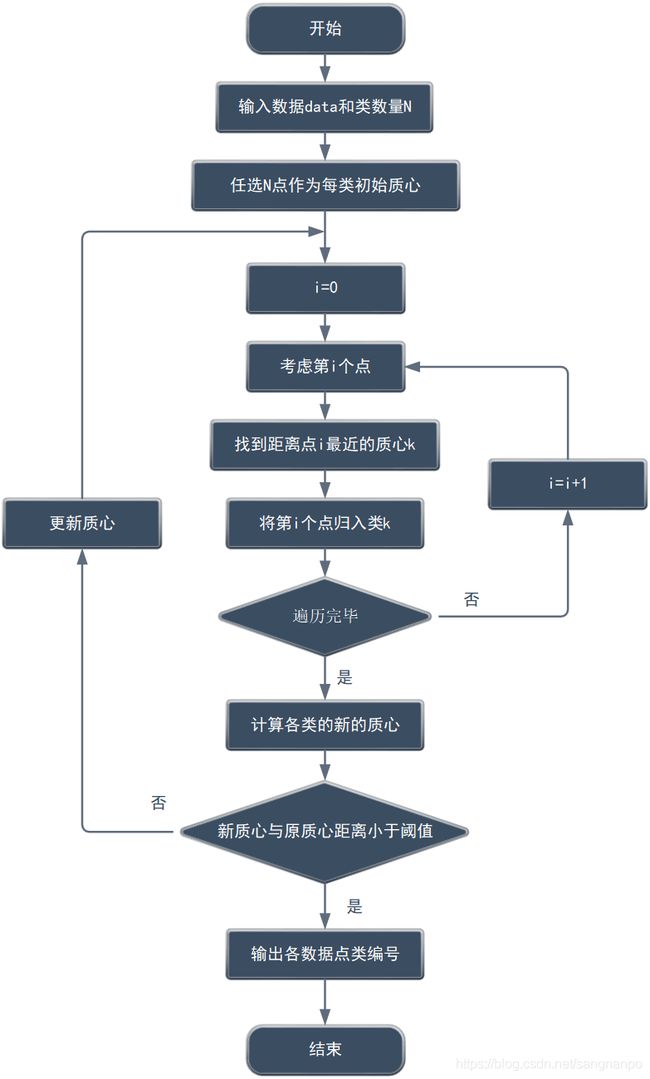
2. k_means聚类原理

k_means聚类流程图如下

3. k_means聚类函数代码

function T = k_means(data, m, num, e)
% 本函数用于k_means聚类
% 输入data为聚类数据，每行一个数据点
% 输入m为簇的数量
% 输入num为最大迭代次数
% 输入e为阈值，指标为质心距离矩阵的迹，即更新前后质心距离之和
% 输出T为数据对应的类别号组成的序列
% 输出文件'.\centroid.txt'，记录迭代次数及每次迭代的各类质心变化情况

% 数据维数
datadim = length(data(1, :));
% 总数据量
n = length(data(:, 1));
% 定义类别标记列表
T = zeros(n, 1);

% 得到初始m个质心
r = randperm(n, m); 
C0 = rand(m, datadim);
for k = 1 : m
    C0(k, :) = data(r(k), :);
end
C1 = zeros(m, datadim);
Num = 0;

% 打开文件
file = fopen('.\centroid.txt', 'wt');
%将写入指针移动至文章的开头
frewind(file);
% 如果两组质心之间的距离矩阵的迹仍大于阈值e，并且迭代次数没超过num，则进行循环
if file > 0
    while (trace(pdist2(C0, C1)) > e) && (Num <= num)
        for i = 1 : n
            mind = pdist2(data(i, :), C0(1, :));
            for j = 1 : m
                if pdist2(data(i, :), C0(j, :)) <= mind
                    T(i) = j;
                    mind = pdist2(data(i, :), C0(j, :));
                end
            end
        end
        % 更新质心
        C1 = C0;
        fprintf(file, '%d\n', Num);
        for j = 1 : m
            for k = 1 : datadim
                fprintf(file, '%f,\t', C0(j, k));
                C0(j, k) = mean(data(T==j, k));
            end
            fprintf(file, '\n');
        end
        Num = Num + 1;
    end
    fclose(file);
end

主函数：

% model_class = 3;
% dim = 3;
% % 期望值
% m = [0, 0, 0;
%     2, 2, 2;
%     -2, -2, -2];
% % 协方差阵
% s(:, :, 1) = [0.2, 0, 0;
%               0, 0.2, 0;
%               0, 0, 0.2];
% s(:, :, 2) = [0.5, 0, 0;
%               0, 0.5, 0;
%               0, 0, 0.5];
% s(:, :, 3) = [0.5, 0, 0;
%               0, 0.5, 0;
%               0, 0, 0.5];
%           
% num = [5000, 5000, 5000];
% data = generate_data_GMM(dim, model_class, m, s, num);
iris = load('iris.txt');
data = iris(:, (1:4));
T = k_means(data, 3, 30, 0.05);

注：主函数给了两个例子，一个是基于高斯分布数据，一个是基于鸢尾花测试数据。这里高斯分布数据用到了笔者自编写的generate_data_GMM函数，这个函数详细说明及代码请查看：
matlab生成多组多维高斯分布数据

4. 其他说明

1. k_means聚类算法简单，学聚类第一个接触的聚类算法几乎都是k_means聚类。k_menas聚类有两大重要的缺点：
   其一：需要知道聚类的类别数量
   其二：可能收敛到局部最优解
   但是类别的数量有方法可以估计出来，估计方法这里不在赘述，读者可查阅其他资料。在不需要实时应用时，也可以多次尝试选择最佳聚类数量。局部最优的情况也可以通过多次聚类来弥补。所以k_means聚类的特点可以归纳为：简单，但是一般够用。
2. 本函数中使用了欧拉距离作为距离的度量，也可以选择其他距离，更改函数代码中的pdist2函数的距离参数即可。