【入门向】k-means聚类函数详解(基于鸢尾花数据集)【MATLAB】
这是一个目录
- k-means聚类函数
-
- 先放例程
- 分段解析
-
- PART1——载入数据集
- PART2——画出数据集分布图
- PART3——kmeans对数据集聚类
- PART4——确定坐标栅格
- PART5——kmeans对网格点聚类
- PART6——作图
- 鸢尾花数据集
k-means聚类函数
先放例程
官方例程点这☜ Train a k-Means Clustering Algorithm.
load fisheriris
X = meas(:,3:4);
figure;
plot(X(:,1),X(:,2),'k*','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)';
rng(1); % For reproducibility
[idx,C] = kmeans(X,3);
% Assigns each node in the grid to the closest centroid
x1 = min(X(:,1)):0.01:max(X(:,1));
x2 = min(X(:,2)):0.01:max(X(:,2));
[x1G,x2G] = meshgrid(x1,x2);
XGrid = [x1G(:),x2G(:)]; % Defines a fine grid on the plot
idx2Region = kmeans(XGrid,3,'MaxIter',1,'Start',C);
% Assigns each node in the grid to the closest centroid
figure;
gscatter(XGrid(:,1),XGrid(:,2),idx2Region,...
[0,0.75,0.75;0.75,0,0.75;0.75,0.75,0],'..');
hold on;
plot(X(:,1),X(:,2),'k*','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)';
legend('Region 1','Region 2','Region 3','Data','Location','SouthEast');
hold off;
分段解析
- 注:“%”段为注释,MATLAB代码好像没办法在markdown编辑器中高亮(小声,也可能是我自己没研究明白QuQ)。
PART1——载入数据集
load fisheriris
X = meas(:,3:4);
加载样本数据并取数据数组的第3,4列存到变量X中。
这一步的目的主要是为了获取样本数据集,还有很多其他类型的数据集可以使用,可以参考这篇博客《一些用于聚类和分类问题的数据集》。
fisheriris——鸢尾花数据集(意为fisher算法的iris数据集),是一类多重变量分析的数据集,样本数量150个,每类50个。通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa(山鸢尾),Versicolour(杂色鸢尾),Virginica(维吉尼亚鸢尾))三个种类中的哪一类。
鸢尾花完整数据集放在文末。
PART2——画出数据集分布图
figure;
plot(X(:,1),X(:,2),'k*','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)';
figure——创建图窗窗口
X(:,1) 表示 X 数组的第一列,X(:,2) 同理。
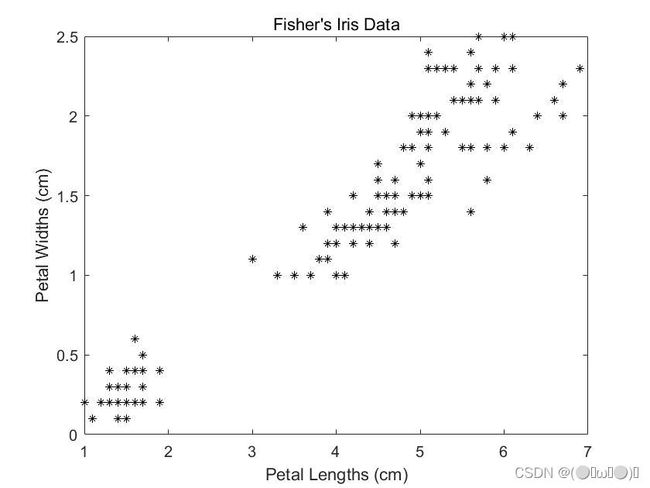
运行 plot 函数产生下图,其中 X 的第一列为横坐标取值,第二列为纵坐标取值。
PART3——kmeans对数据集聚类
rng(1); % For reproducibility
[idx,C] = kmeans(X,3);
rng——控制随机数生成器
常用语法有:
rng(seed)
rng(seed,generator)
s = rng
指定 MATLAB® 随机数生成器的种子。例如,rng(1) 使用种子 1 初始化梅森旋转生成器。相关例程请参考《rng控制随机数生成器》
kmeans——k均值聚类
常用语法有:
idx = kmeans(X,k)
idx = kmeans(X,k,Name,Value)
[idx,C] = kmeans(___)
[idx,C,sumd] = kmeans(___)
[idx,C,sumd,D] = kmeans(___)
此处idx是长度为N×1的标号数组,C是聚类中心坐标值组成的数组,因此处聚类组数k=3,所处空间为二维平面,因此C的大小为3×2
PART4——确定坐标栅格
% Assigns each node in the grid to the closest centroid
x1 = min(X(:,1)):0.01:max(X(:,1));
x2 = min(X(:,2)):0.01:max(X(:,2));
[x1G,x2G] = meshgrid(x1,x2);
XGrid = [x1G(:),x2G(:)]; % Defines a fine grid on the plot
x1,x2用于决定坐标范围,取0.01为最小间距。
使用“数据游标”工具,可以更加直观地看到数据横纵轴上下限。
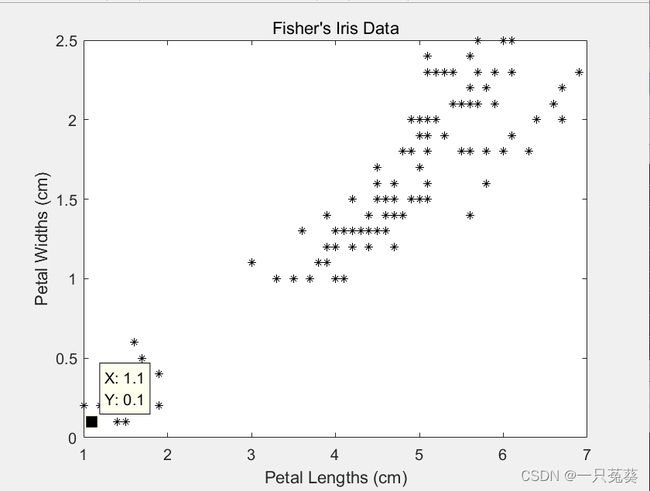
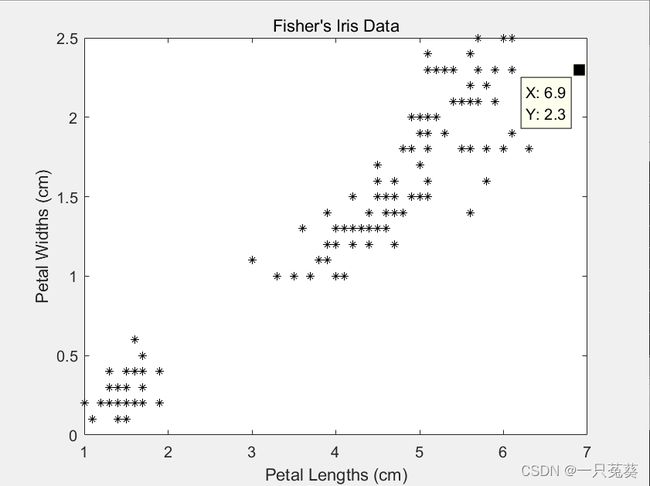

x ∈ [ 1 , 6.9 ] y ∈ [ 0.1 , 2.5 ] x \in [1,6.9] \\ y \in [0.1, 2.5] x∈[1,6.9]y∈[0.1,2.5]
以0.01为间距划分,可以计算出x1和x2的长度:
x 1 = ( 6.9 − 1 ) / 0.01 + 1 = 591 x 2 = ( 2.5 − 0.1 ) / 0.01 + 1 = 241 x1=(6.9-1)/0.01+1=591\\x2=(2.5-0.1)/0.01+1=241 x1=(6.9−1)/0.01+1=591x2=(2.5−0.1)/0.01+1=241
在工作区中可以看到变量长度与计算结果相同:
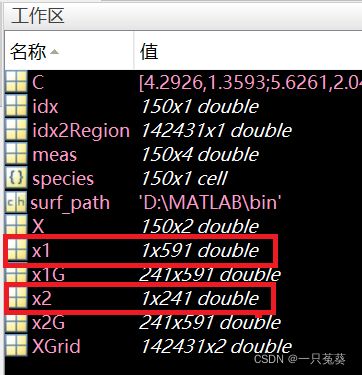
mshgrid建立二维网格
PART5——kmeans对网格点聚类
idx2Region = kmeans(XGrid,3,'MaxIter',1,'Start',C);
% Assigns each node in the grid to the closest centroid
MaxIter是指kmeans算法最大迭代次数,此处最大迭代次数为1。
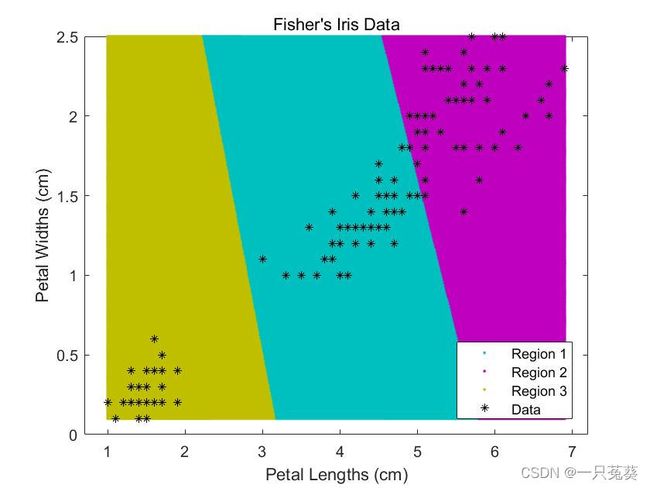
PART6——作图
figure;
gscatter(XGrid(:,1),XGrid(:,2),idx2Region,...
[0,0.75,0.75;0.75,0,0.75;0.75,0.75,0],'..');
hold on;
plot(X(:,1),X(:,2),'k*','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)';
legend('Region 1','Region 2','Region 3','Data','Location','SouthEast');
hold off;
gscatter——散点图绘制工具
常用语法有:
gscatter(x,y,g)
gscatter(x,y,g,clr,sym,siz)
gscatter(x,y,g,clr,sym,siz,doleg)
gscatter(x,y,g,clr,sym,siz,doleg,xnam,ynam)
gscatter(ax,___)
h = gscatter(___)
值得注意的是:咋此处gscatter并不是用来绘制“散点图”,而是利用带有颜色的密集散点形成带颜色的区域。因为region取值足够大,所以散点足够密集(就成一片了0m0)。

[0,0.75,0.75;0.75,0,0.75;0.75,0.75,0]是三个RGB颜色取值,对应颜色分别为:


gscatter(XGrid(:,1),XGrid(:,2),idx2Region,...
[0,0.75,0.75;0.75,0,0.75;0.75,0.75,0],'..');
这个’…‘指的(应该)是散点的形状,替换成’.'输出的图片一样。(我怀疑这里是写例程的老师手抖了,多大了一个.【狗头保命】)
legend——在坐标区上添加图例
常用语法有:
legend
legend(label1,…,labelN)
legend(labels)
legend(subset,___)
legend(target,___)
鸢尾花数据集
| 萼片长(sepal length) | 萼片宽(sepal width) | 花瓣长(petal length) | 花瓣宽(petal width) |
|---|---|---|---|
| 5.10 | 3.50 | 1.40 | 0.20 |
| 4.90 | 3.00 | 1.40 | 0.20 |
| 4.70 | 3.20 | 1.30 | 0.20 |
| 4.60 | 3.10 | 1.50 | 0.20 |
| 5.00 | 3.60 | 1.40 | 0.20 |
| 5.40 | 3.90 | 1.70 | 0.40 |
| 4.60 | 3.40 | 1.40 | 0.30 |
| 5.00 | 3.40 | 1.50 | 0.20 |
| 4.40 | 2.90 | 1.40 | 0.20 |
| 4.90 | 3.10 | 1.50 | 0.10 |
| 5.40 | 3.70 | 1.50 | 0.20 |
| 4.80 | 3.40 | 1.60 | 0.20 |
| 4.80 | 3.00 | 1.40 | 0.10 |
| 4.30 | 3.00 | 1.10 | 0.10 |
| 5.80 | 4.00 | 1.20 | 0.20 |
| 5.70 | 4.40 | 1.50 | 0.40 |
| 5.40 | 3.90 | 1.30 | 0.40 |
| 5.10 | 3.50 | 1.40 | 0.30 |
| 5.70 | 3.80 | 1.70 | 0.30 |
| 5.10 | 3.80 | 1.50 | 0.30 |
| 5.40 | 3.40 | 1.70 | 0.20 |
| 5.10 | 3.70 | 1.50 | 0.40 |
| 4.60 | 3.60 | 1.00 | 0.20 |
| 5.10 | 3.30 | 1.70 | 0.50 |
| 4.80 | 3.40 | 1.90 | 0.20 |
| 5.00 | 3.00 | 1.60 | 0.20 |
| 5.00 | 3.40 | 1.60 | 0.40 |
| 5.20 | 3.50 | 1.50 | 0.20 |
| 5.20 | 3.40 | 1.40 | 0.20 |
| 4.70 | 3.20 | 1.60 | 0.20 |
| 4.80 | 3.10 | 1.60 | 0.20 |
| 5.40 | 3.40 | 1.50 | 0.40 |
| 5.20 | 4.10 | 1.50 | 0.10 |
| 5.50 | 4.20 | 1.40 | 0.20 |
| 4.90 | 3.10 | 1.50 | 0.20 |
| 5.00 | 3.20 | 1.20 | 0.20 |
| 5.50 | 3.50 | 1.30 | 0.20 |
| 4.90 | 3.60 | 1.40 | 0.10 |
| 4.40 | 3.00 | 1.30 | 0.20 |
| 5.10 | 3.40 | 1.50 | 0.20 |
| 5.00 | 3.50 | 1.30 | 0.30 |
| 4.50 | 2.30 | 1.30 | 0.30 |
| 4.40 | 3.20 | 1.30 | 0.20 |
| 5.00 | 3.50 | 1.60 | 0.60 |
| 5.10 | 3.80 | 1.90 | 0.40 |
| 4.80 | 3.00 | 1.40 | 0.30 |
| 5.10 | 3.80 | 1.60 | 0.20 |
| 4.60 | 3.20 | 1.40 | 0.20 |
| 5.30 | 3.70 | 1.50 | 0.20 |
| 5.00 | 3.30 | 1.40 | 0.20 |
| 7.00 | 3.20 | 4.70 | 1.40 |
| 6.40 | 3.20 | 4.50 | 1.50 |
| 6.90 | 3.10 | 4.90 | 1.50 |
| 5.50 | 2.30 | 4.00 | 1.30 |
| 6.50 | 2.80 | 4.60 | 1.50 |
| 5.70 | 2.80 | 4.50 | 1.30 |
| 6.30 | 3.30 | 4.70 | 1.60 |
| 4.90 | 2.40 | 3.30 | 1.00 |
| 6.60 | 2.90 | 4.60 | 1.30 |
| 5.20 | 2.70 | 3.90 | 1.40 |
| 5.00 | 2.00 | 3.50 | 1.00 |
| 5.90 | 3.00 | 4.20 | 1.50 |
| 6.00 | 2.20 | 4.00 | 1.00 |
| 6.10 | 2.90 | 4.70 | 1.40 |
| 5.60 | 2.90 | 3.60 | 1.30 |
| 6.70 | 3.10 | 4.40 | 1.40 |
| 5.60 | 3.00 | 4.50 | 1.50 |
| 5.80 | 2.70 | 4.10 | 1.00 |
| 6.20 | 2.20 | 4.50 | 1.50 |
| 5.60 | 2.50 | 3.90 | 1.10 |
| 5.90 | 3.20 | 4.80 | 1.80 |
| 6.10 | 2.80 4.00 | 1.30 | |
| 6.30 | 2.50 | 4.90 | 1.50 |
| 6.10 | 2.80 | 4.70 | 1.20 |
| 6.40 | 2.90 | 4.30 | 1.30 |
| 6.60 | 3.00 | 4.40 | 1.40 |
| 6.80 | 2.80 | 4.80 | 1.40 |
| 6.70 | 3.00 | 5.00 | 1.70 |
| 6.00 | 2.90 | 4.50 | 1.50 |
| 5.70 | 2.60 | 3.50 | 1.00 |
| 5.50 | 2.40 | 3.80 | 1.10 |
| 5.50 | 2.40 | 3.70 | 1.00 |
| 5.80 | 2.70 | 3.90 | 1.20 |
| 6.00 | 2.70 | 5.10 | 1.60 |
| 5.40 | 3.00 | 4.50 | 1.50 |
| 6.00 | 3.40 | 4.50 | 1.60 |
| 6.70 | 3.10 | 4.70 | 1.50 |
| 6.30 | 2.30 | 4.40 | 1.30 |
| 5.60 | 3.00 | 4.10 | 1.30 |
| 5.50 | 2.50 | 4.00 | 1.30 |
| 5.50 | 2.60 | 4.40 | 1.20 |
| 6.10 | 3.00 | 4.60 | 1.40 |
| 5.80 | 2.60 | 4.00 | 1.20 |
| 5.00 | 2.30 | 3.30 | 1.00 |
| 5.60 | 2.70 | 4.20 | 1.30 |
| 5.70 | 3.00 | 4.20 | 1.20 |
| 5.70 | 2.90 | 4.20 | 1.30 |
| 6.20 | 2.90 | 4.30 | 1.30 |
| 5.10 | 2.50 | 3.00 | 1.10 |
| 5.70 | 2.80 | 4.10 | 1.30 |
| 6.30 | 3.30 | 6.00 | 2.50 |
| 5.80 | 2.70 | 5.10 | 1.90 |
| 7.10 | 3.00 | 5.90 | 2.10 |
| 6.30 | 2.90 | 5.60 | 1.80 |
| 6.50 | 3.00 | 5.80 | 2.20 |
| 7.60 | 3.00 | 6.60 | 2.10 |
| 4.90 | 2.50 | 4.50 | 1.70 |
| 7.30 | 2.90 | 6.30 | 1.80 |
| 6.70 | 2.50 | 5.80 | 1.80 |
| 7.20 | 3.60 | 6.10 | 2.50 |
| 6.50 | 3.20 | 5.10 | 2.00 |
| 6.40 | 2.70 | 5.30 | 1.90 |
| 6.80 | 3.00 | 5.50 | 2.10 |
| 5.70 | 2.50 | 5.00 | 2.00 |
| 5.80 | 2.80 | 5.10 | 2.40 |
| 6.40 | 3.20 | 5.30 | 2.30 |
| 6.50 | 3.00 | 5.50 | 1.80 |
| 7.70 | 3.80 | 6.70 | 2.20 |
| 7.70 | 2.60 | 6.90 | 2.30 |
| 6.00 | 2.20 | 5.00 | 1.50 |
| 6.90 | 3.20 | 5.70 | 2.30 |
| 5.60 | 2.80 | 4.90 | 2.00 |
| 7.70 | 2.80 | 6.70 | 2.00 |
| 6.30 | 2.70 | 4.90 | 1.80 |
| 6.70 | 3.30 | 5.70 | 2.10 |
| 7.20 | 3.20 | 6.00 | 1.80 |
| 6.20 | 2.80 | 4.80 | 1.80 |
| 6.10 | 3.00 | 4.90 | 1.80 |
| 6.40 | 2.80 | 5.60 | 2.10 |
| 7.20 | 3.00 | 5.80 | 1.60 |
| 7.40 | 2.80 | 6.10 | 1.90 |
| 7.90 | 3.80 | 6.40 | 2.00 |
| 6.40 | 2.80 | 5.60 | 2.20 |
| 6.30 | 2.80 | 5.10 | 1.50 |
| 6.10 | 2.60 | 5.60 | 1.40 |
| 7.70 | 3.00 | 6.10 | 2.30 |
| 6.30 | 3.40 | 5.60 | 2.40 |
| 6.40 | 3.10 | 5.50 | 1.80 |
| 6.00 | 3.00 | 4.80 | 1.80 |
| 6.90 | 3.10 | 5.40 | 2.10 |
| 6.70 | 3.10 | 5.60 | 2.40 |
| 6.90 | 3.10 | 5.10 | 2.30 |
| 5.80 | 2.70 | 5.10 | 1.90 |
| 6.80 | 3.20 | 5.90 | 2.30 |
| 6.70 | 3.30 | 5.70 | 2.50 |
| 6.70 | 3.00 | 5.20 | 2.30 |
| 6.30 | 2.50 | 5.00 | 1.90 |
| 6.50 | 3.00 | 5.20 | 2.00 |
| 6.20 | 3.40 | 5.40 | 2.30 |
| 5.90 | 3.00 | 5.10 | 1.80 |