Phoenixtree_DongZhao

MyDLNote - Attention: ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks

MyDLNote - Attention: [2020CVPR] ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks

Qilong Wang1 , Banggu Wu1 , Pengfei Zhu1 , Peihua Li2 , Wangmeng Zuo3 , Qinghua Hu1,∗

1 Tianjin Key Lab of Machine Learning, College of Intelligence and Computing, Tianjin University, China

2 Dalian University of Technology, China

3 Harbin Institute of Technology, China

【前言】本文的贡献是改变了对传统 SE 的认知，从中学到的收货是，对于一个网络，不要盲目顺从其中的细节，动手做些真实的实验，能得到新的结论和发现。

语言写作只能说正常。

MyDLNote - Attention: [2020CVPR] ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks

Abstract

Introduction

Proposed Method

Revisiting Channel Attention in SE Block

Efficient Channel Attention (ECA) Module

Coverage of Local Cross-Channel Interaction

ECA Module for Deep CNNs

Code

Abstract

Recently, channel attention mechanism has demonstrated to offer great potential in improving the performance of deep convolutional neural networks (CNNs). However, most existing methods dedicate to developing more sophisticated attention modules for achieving better performance, which inevitably increase model complexity. To overcome the paradox of performance and complexity trade-off, this paper proposes an Efficient Channel Attention (ECA) module, which only involves a handful of parameters while bringing clear performance gain.

本文的 motivation：传统的方法致力于复杂的注意力设计，而本文提出的方法只引入少量参数，却带来明显的性能增益。

By dissecting the channel attention module in SENet, we empirically show avoiding dimensionality reduction is important for learning channel attention, and appropriate cross-channel interaction can preserve performance while significantly decreasing model complexity.

本文的核心思想：避免降维对于学习通道注意是很重要的；适当的跨通道交互可以在显著降低模型复杂度的同时保持性能。

Therefore, we propose a local cross-channel interaction strategy without dimensionality reduction, which can be efficiently implemented via 1D convolution. Furthermore, we develop a method to adaptively select kernel size of 1D convolution, determining coverage of local cross-channel interaction.

本文的核心工作：

提出了一种无降维的局部跨通道交互策略，该策略可以通过一维卷积有效地实现；

建立了一种自适应选择一维卷积核大小的方法，确定了局部跨通道相互作用的覆盖范围。

The proposed ECA module is efficient yet effective, e.g., the parameters and computations of our modules against backbone of ResNet50 are 80 vs. 24.37M and 4.7e-4 GFLOPs vs. 3.86 GFLOPs, respectively, and the performance boost is more than 2% in terms of Top-1 accuracy. We extensively evaluate our ECA module on image classification, object detection and instance segmentation with backbones of ResNets and MobileNetV2. The experimental results show our module is more efficient while performing favorably against its counterparts.

实验结果。

Introduction

讲清楚一个故事：

Recently, incorporation of channel attention into convolution blocks has attracted a lot of interests, showing great potential in performance improvement [14, 33, 13, 4, 9, 18, 7].

第一段：大背景介绍 --- attention 用在卷积模块中获得很大成果。

[4] A2 -Nets: Double attention networks. In NIPS, 2018.

[7] Dual attention network for scene segmentation. In CVPR, 2019.

[9] Global second-order pooling convolutional networks. In CVPR, 2019.

[13] Gather-excite: Exploiting feature context in convolutional neural networks. In NeurIPS, 2018.

[14] Squeeze-and-excitation networks. In CVPR, 2018.

[18] Channel locality block: A variant of squeeze-andexcitation. arXiv, 1901.01493, 2019.

[33] CBAM: Convolutional block attention module. In ECCV, 2018.

Following the setting of squeeze (i.e., feature aggregation) and excitation (i.e., feature recalibration) in SENet [14], some researches improve SE block by capturing more sophisticated channel-wise dependencies [33, 4, 9, 7] or by combining with additional spatial attention [33, 13, 7]. Although these methods have achieved higher accuracy, they often bring higher model complexity and suffer from heavier computational burden. Different from the aforementioned methods that achieve better performance at the cost of higher model complexity, this paper focuses instead on a question: Can one learn effective channel attention in a more efficient way?

第二段：提出问题 --- 但是，这些成果都是在设计更复杂的通道 attention 或添加复杂的空间 attention。本文就想，能不能提出一个不用明显增加复杂度，而提高 attention 性能的方法呢？

To answer this question, we first revisit the channel attention module in SENet. Specifically, given the input features, SE block first employs a global average pooling for each channel independently, then two fully-connected (FC) layers with non-linearity followed by a Sigmoid function are used to generate channel weights. The two FC layers are designed to capture non-linear cross-channel interaction, which involve dimensionality reduction for controlling model complexity. Although this strategy is widely used in subsequent channel attention modules [33, 13, 9], our empirical studies show dimensionality reduction brings side effect on channel attention prediction, and it is inefficient and unnecessary to capture dependencies across all channels.

第三段：提出本文的核心发现 --- SE 的两个问题：

1. FC 中间隐含层降维：降维对同道注意力预测有负面影响；（这个问题大家都知道）

2. FC 层学习通道之间的关系：跨所有通道捕获依赖项是低效且不必要的。（这个问题我是第一次听说，还是蛮吸引人的）

Therefore, this paper proposes an Efficient Channel Attention (ECA) module for deep CNNs, which avoids dimensionality reduction and captures cross-channel interaction in an efficient way. As illustrated in Figure 2, after channel-wise global average pooling without dimensionality reduction, our ECA captures local cross-channel interaction by considering every channel and its neighbors. Such method is proven to guarantee both efficiency and effectiveness. Note that our ECA can be efficiently implemented by fast 1D convolution of size , where kernel size represents the coverage of local cross-channel interaction, i.e., how many neighbors participate in attention prediction of one channel. To avoid manual tuning of via cross-validation, we develop a method to adaptively determine , where coverage of interaction (i.e., kernel size ) is proportional to channel dimension. As shown in Figure 1 and Table 3, as opposed to the backbone models [11], deep CNNs with our ECA module (called ECA-Net) introduce very few additional parameters and negligible computations, while bringing notable performance gain. For example, for ResNet-50 with 24.37M parameters and 3.86 GFLOPs, the additional parameters and computations of ECA-Net50 are 80 and 4.7e- 4 GFLOPs, respectively; meanwhile, ECA-Net50 outperforms ResNet-50 by 2.28% in terms of Top-1 accuracy.

第四段：针对发现，提出解决方案 --- 1）避免 FC 中的降维，以有效的方式捕获跨通道交互；2）自动调整的大小。

具体地，1）就是将感知器换成局部卷积层，输出与输入维度相同；虽然很简单，但确实是常规思维的突破；

2）交互的范围(即，内核大小)与通道维数成正比。

Figure 2. Diagram of our efficient channel attention (ECA) module. Given the aggregated features obtained by global average pooling (GAP), ECA generates channel weights by performing a fast 1D convolution of size k, where k is adaptively determined via a mapping of channel dimension C.

Table 1 summarizes existing attention modules in terms of whether channel dimensionality reduction (DR), cross-channel interaction and lightweight model, where we can see that our ECA module learn effective channel attention by avoiding channel dimensionality reduction while capturing cross-channel interaction in an extremely lightweight way. To evaluate our method, we conduct experiments on ImageNet-1K [6] and MS COCO [23] in a variety of tasks using different deep CNN architectures.

第五段：提出解决方案和其它方法的直观对比，可以赢得渎者对本文方法的好感和信任。

Table 1. Comparison of existing attention modules in terms of whether no channel dimensionality reduction (No DR), crosschannel interaction and less parameters than SE (indicated by lightweight) or not.

The contributions of this paper are summarized as follows. (1) We dissect the SE block and empirically demonstrate avoiding dimensionality reduction and appropriate cross-channel interaction are important to learn effective and efficient channel attention, respectively. (2) Based on above analysis, we make an attempt to develop an extremely lightweight channel attention module for deep CNNs by proposing an Efficient Channel Attention (ECA), which increases little model complexity while bringing clear improvement. (3) The experimental results on ImageNet-1K and MS COCO demonstrate our method has lower model complexity than state-of-the-arts while achieving very competitive performance.

第六段：总结贡献：(1)我们解剖了SE块，并通过实证证明避免降维和适当的跨通道交互对学习对于有效的和高效的通道注意是重要的。(2)基于以上分析，我们提出了一种有效的通道注意(ECA)方法，尝试为深度CNNs开发一种非常轻量级的通道注意模块，该方法在提高模型复杂度的同时，也带来了明显的改进。(3)在ImageNet-1K和MS COCO上的实验结果表明，我们的方法在获得极具竞争力的性能的同时，具有较低的模型复杂度。

Proposed Method

In this section, we first revisit the channel attention module in SENet [14] (i.e., SE block). Then, we make a empirical diagnosis of SE block by analyzing effects of dimensionality reduction and cross-channel interaction. This motivates us to propose our ECA module. In addition, we develop a method to adaptively determine parameter of our ECA, and finally show how to adopt it for deep CNNs.

Revisiting Channel Attention in SE Block

Let the output of one convolution block be $X \in \mathbb{R}^{W\times H\times C}$ , where , and are width, height and channel dimension (i.e., number of filters). Accordingly, the weights of channels in SE block can be computed as

$\omega = \sigma(f_{\{W_1,W_2\}}(g(X)))$ , (1)

where $g(X)=(WH)^{-1}\sum^{W,H}_{i=1,j=1}X_{i,j}$ is channel-wise global average pooling (GAP) and $\sigma$ is a Sigmoid function. Let

, $f_{\{W_1,W_2\}}$ takes the form

$f_{\{W_1,W_2\}}(y) = W_2ReLU(W_1y)$ , (2)

where ReLU indicates the Rectified Linear Unit. To avoid high model complexity, sizes of and are set to $C \times ( C/r )$ and $( C/r ) \times C$ , respectively. We can see that $f_{\{W_1,W_2\}}$ involves all parameters of channel attention block. While dimensionality reduction in Eq. (2) can reduce model complexity, it destroys the direct correspondence between channel and its weight. For example, one single FC layer predicts weight of each channel using a linear combination of all channels. But Eq. (2) first projects channel features into a low-dimensional space and then maps them back, making correspondence between channel and its weight be indirect.

提出了SE的问题：Eq.(2)首先将信道特征投影到低维空间中，然后将其映射回来，使得信道与其权值之间的对应是间接的。

Efficient Channel Attention (ECA) Module

Avoiding Dimensionality Reduction

As discussed above, dimensionality reduction in Eq. (2) makes correspondence between channel and its weight be indirect. To verify its effect, we compare the original SE block with its three variants (i.e., SE-Var1, SE-Var2 and SEVar3), all of which do not perform dimensionality reduction. As presented in Table 2, SE-Var1 with no parameter is still superior to the original network, indicating channel attention has ability to improve performance of deep CNNs. Meanwhile, SE-Var2 learns the weight of each channel independently, which is slightly superior to SE block while involving less parameters. It may suggest that channel and its weight needs a direct correspondence while avoiding dimensionality reduction is more important than consideration of nonlinear channel dependencies. Additionally, SE-Var3 employing one single FC layer performs better than two FC layers with dimensionality reduction in SE block. All of above results clearly demonstrate avoiding dimensionality reduction is helpful to learn effective channel attention. Therefore, we develop our ECA module without channel dimensionality reduction.

这小节给出了重要实验观察，即：

SE-Var1：没有参数的 SE-Var1 仍优于原网络（这句是不是写错了？），说明信道注意有能力提高深度CNNs的性能。

SE-Var2：SE- var2 独立学习每个通道的权值（depth-wise 卷积吗？），在参数较少的情况下略优于 SE 块。

SE-Var3：使用单个 FC 层的 SE- var3 要比使用两个降维的 FC 层的 SE 块性能更好。

以上结果清楚地表明，避免降维有助于学习有效的渠道注意。因此，我们开发的ECA模块没有降低通道维数。

Table 2. Comparison of various channel attention modules using ResNet-50 as backbone model on ImageNet. #.Param. indicates number of parameters of the channel attention module; $\odot$ indicates element-wise product; GC and C1D indicate group convolutions and 1D convolution, respectively; k is kernel size of C1D.

Local Cross-Channel Interaction

Given the aggregated feature $y \in \mathbb{R}^C$ without dimensionality reduction, channel attention can be learned by $\omega =\sigma(Wy)$ , where is a $C \times C$ parameter matrix. In particular, for SE-Var2 and SE-Var3 we have

where $W_{var2}$ for SE-Var2 is a diagonal matrix, involving parameters; $W_{var3}$ for SE-Var3 is a full matrix, involving $C \times C$ parameters. As shown in Eq. (4), the key difference is that SE-Var3 considers cross-channel interaction while SE-Var2 does not, and consequently SE-Var3 achieves better performance. This result indicates that cross-channel interaction is beneficial to learn channel attention. However, SE-Var3 requires a mass of parameters, leading to high model complexity, especially for large channel numbers.

上一小节说明了无缩放的 SE-Var2 和 SE-Var3 效果最好。这一段呢，就解释一下，为啥 SE-Var3 优于 SE-Var2：SE-Var3考虑跨通道交互，而SE-Var2不考虑，因此SE-Var3获得了更好的性能。

进一步推理，那把 SE-Var2 和 SE-Var3 结合一下，会好吗？

A possible compromise between SE-Var2 and SE-Var3 is extension of $W_{var2}$ to a block diagonal matrix, i.e.,

where Eq. (5) divides channel into groups each of which includes channels, and learns channel attention in each group independently, which captures cross-channel interaction in a local manner. Accordingly, it involves parameters. From perspective of convolution, SE-Var2, SEVar3 and Eq. (5) can be regarded as a depth-wise separable convolution, a FC layer and group convolutions, respectively. Here, SE block with group convolutions (SE-GC) is indicated by $\sigma(GC_G(y)) = \sigma(W_Gy)$ . However, as shown in [24], excessive group convolutions will increase memory access cost and so decrease computational efficiency. Furthermore, as shown in Table 2, SE-GC with varying groups bring no gain over SE-Var2, indicating it is not an effective scheme to capture local cross-channel interaction. The reason may be that SE-GC completely discards dependences among different groups.

SE-Var2 和 SE-Var3 结合的方法，就是用组卷积方法 --- SE-GC。

虽然很巧妙，但效果不好。原因可能是SE-GC完全抛弃了不同组之间的依赖性。

In this paper, we explore another method to capture local cross-channel interaction, aiming at guaranteeing both efficiency and effectiveness. Specifically, we employ a band matrix to learn channel attention, and has

Clearly, in Eq. (6) involves $k \times C$ parameters, which is usually less than those of Eq. (5). Furthermore, Eq. (6) avoids complete independence among different groups in Eq. (5). As compared in Table 2, the method in Eq. (6) (namely ECA-NS) outperforms SE-GC of Eq. (5). As for Eq. (6), the weight of is calculated by only considering interaction between and its neighbors, i.e.,

where $\Omega_i^k$ indicates the set of adjacent channels of .

A more efficient way is to make all channels share the same learning parameters, i.e.,

SE-GC 效果不好的原因是交互性不好，那就提一个交互性好的方法，就是公式（6）。

我分析觉得这是一个分成个的 $1\times k$ 的卷积，且相邻卷积的中心位置步进为 1。

进一步为了减少参数，所有的卷积共享参数，即，这是一个 $1\times k$ 、步进为 1 的卷积。

Note that such strategy can be readily implemented by a fast 1D convolution with kernel size of , i.e.,

$\omega = \sigma(C1D_k(y))$ , (9)

where indicates 1D convolution. Here, the method in Eq. (9) is called by efficient channel attention (ECA) module, which only involves parameters. As presented in Table 2, our ECA module with achieves similar results with SE-var3 while having much lower model complexity, which guarantees both efficiency and effectiveness by appropriately capturing local cross-channel interaction.

惊讶不！做了半天实验，推导了半天，最后就是一个 $1\times 3$ 卷积代替了原来的 FC 层！！！

这就是 efficient channel attention (ECA) module。结论很简单，但过程比较细致。

当然了，这个 3 是实验值，下面提出了一种自适应的方法，来确定卷积核的长度。

Coverage of Local Cross-Channel Interaction

Since our ECA module (9) aims at appropriately capturing local cross-channel interaction, so the coverage of interaction (i.e., kernel size k of 1D convolution) needs to be determined. The optimized coverage of interaction could be tuned manually for convolution blocks with different channel numbers in various CNN architectures. However, manual tuning via cross-validation will cost a lot of computing resources. Group convolutions have been successfully adopted to improve CNN architectures [37, 34, 16], where high-dimensional (low-dimensional) channels involve long range (short range) convolutions given the fixed number of groups. Sharing the similar philosophy, it is reasonable that the coverage of interaction (i.e., kernel size of 1D convolution) is proportional to channel dimension . In other words, there may exist a mapping $\varphi$ between and :

$C = \varphi (k)$ . (10)

The simplest mapping is a linear function, i.e., $\varphi (k) = \gamma \ast k- b$ .

交互的覆盖范围应该与输入通道个数成正比，然后给出了最简单的线性形式 $\varphi (k) = \gamma \ast k- b$ 。

[16] Deep roots: Improving cnn efficiency with hierarchical filter groups. In CVPR, 2017

[34] Aggregated residual transformations for deep neural networks. In CVPR, 2017.

[37] Interleaved group convolutions. In ICCV, 2017.

However, the relations characterized by linear function are too limited. On the other hand, it is well known that channel dimension C (i.e., number of filters) usually is set to power of 2. Therefore, we introduce a possible solution by extending the linear function $\varphi (k) = \gamma \ast k- b$ to a non-linear one, i.e.,

$C = \varphi (k) = 2^{(\gamma \ast k-b)}$ . (11)

Then, given channel dimension , kernel size can be adaptively determined by

where $|t|_{odd}$ indicates the nearest odd number of . In this paper, we set $\gamma$ and to 2 and 1 throughout all the experiments, respectively. Clearly, through the mapping $\Psi$ , high-dimensional channels have longer range interaction while low-dimensional ones undergo shorter range interaction by using a non-linear mapping.

但是呢，线性的方式过于简单，或者说不能很好地拟合交互覆盖范围与输入通道数之间的潜在关系。

考虑到一般都是 2 的幂次方，因此，设计了非线性关系表达式：

$C = \varphi (k) = 2^{(\gamma \ast k-b)}$

最后，反求，当然，为奇数。

$\gamma=2, ~~ b=1$ 。

ECA Module for Deep CNNs

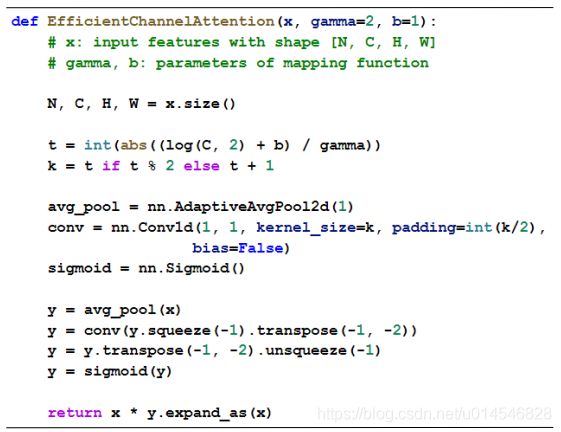
Figure 2 illustrates the overview of our ECA module. After aggregating convolution features using GAP without dimensionality reduction, ECA module first adaptively determines kernel size , and then performs 1D convolution followed by a Sigmoid function to learn channel attention. For applying our ECA to deep CNNs, we replace SE block by our ECA module following the same configuration in [14]. The resulting networks are named by ECA-Net. Figure 3 gives PyTorch code of our ECA. 4.

为了将ECA应用到深度CNNs，用ECA模块替换SE块，在[14]中使用相同的配置。

[14] Densely connected convolutional networks. In CVPR, 2017.

Code

Figure 3. PyTorch code of our ECA module.

实验部分等用的时候再分析吧。。。【持续更新。。。】

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
将cmd中命令输出保存为txt文本文件落难Coder Windows cmd window
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
JavaScript 中，深拷贝（Deep Copy）和浅拷贝（Shallow Copy）跳房子的前端前端面试 javascript 开发语言 ecmascript
在JavaScript中，深拷贝（DeepCopy）和浅拷贝（ShallowCopy）是用于复制对象或数组的两种不同方法。了解它们的区别和应用场景对于避免潜在的bugs和高效地处理数据非常重要。以下是对深拷贝和浅拷贝的详细解释，包括它们的概念、用途、优缺点以及实现方式。1.浅拷贝（ShallowCopy）概念定义：浅拷贝是指创建一个新的对象或数组，其中包含了原对象或数组的基本数据类型的值和对引用数
推荐3家毕业AI论文可五分钟一键生成！文末附免费教程！小猪包333 写论文人工智能 AI写作深度学习计算机视觉
在当前的学术研究和写作领域，AI论文生成器已经成为许多研究人员和学生的重要工具。这些工具不仅能够帮助用户快速生成高质量的论文内容，还能进行内容优化、查重和排版等操作。以下是三款值得推荐的AI论文生成器：千笔-AIPassPaper、懒人论文以及AIPaperPass。千笔-AIPassPaper千笔-AIPassPaper是一款基于深度学习和自然语言处理技术的AI写作助手，旨在帮助用户快速生成高质
AI大模型的架构演进与最新发展季风泯灭的季节 AI大模型应用技术二人工智能架构
随着深度学习的发展，AI大模型（LargeLanguageModels,LLMs）在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进，包括从Transformer的提出到GPT、BERT、T5等模型的历史演变，并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍：Transformer的核心原理Transformer架构的背景在Transfo
[实践应用] 深度学习之模型性能评估指标 YuanDaima2048 深度学习工具使用深度学习人工智能损失函数性能评估 pytorch python 机器学习
文章总览：YuanDaiMa2048博客文章总览深度学习之模型性能评估指标分类任务回归任务排序任务聚类任务生成任务其他介绍在机器学习和深度学习领域，评估模型性能是一项至关重要的任务。不同的学习任务需要不同的性能指标来衡量模型的有效性。以下是对一些常见任务及其相应的性能评估指标的详细解释和总结。分类任务分类任务是指模型需要将输入数据分配到预定义的类别或标签中。以下是分类任务中常用的性能指标：准确率(
[实践应用] 深度学习之优化器 YuanDaima2048 深度学习工具使用 pytorch 深度学习人工智能机器学习 python 优化器
文章总览：YuanDaiMa2048博客文章总览深度学习之优化器1.随机梯度下降（SGD）2.动量优化（Momentum）3.自适应梯度（Adagrad）4.自适应矩估计（Adam）5.RMSprop总结其他介绍在深度学习中，优化器用于更新模型的参数，以最小化损失函数。常见的优化函数有很多种，下面是几种主流的优化器及其特点、原理和PyTorch实现：1.随机梯度下降（SGD）原理:随机梯度下降通过
生成式地图制图 Bwywb_3 深度学习机器学习深度学习生成对抗网络
生成式地图制图（GenerativeCartography）是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统（GIS）技术与现代生成模型（如深度学习、GANs等），能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点：自动化生成：通过算法和模型，系统能够根据输入的地理或空间数据自动生成地图，而无需人工逐
深度 Qlearning：在直播推荐系统中的应用 AGI通用人工智能之禅程序员提升自我硅基计算碳基计算认知计算生物计算深度学习神经网络大数据 AIGC AGI LLM Java Python 架构设计 Agent 程序员实现财富自由
深度Q-learning：在直播推荐系统中的应用关键词：深度Q-learning,强化学习,直播推荐系统,个性化推荐1.背景介绍1.1问题的由来随着互联网技术的飞速发展,直播平台如雨后春笋般涌现。面对海量的直播内容,用户很难快速找到自己感兴趣的内容。因此,个性化推荐系统在直播平台中扮演着越来越重要的角色。1.2研究现状目前,主流的个性化推荐算法包括协同过滤、基于内容的推荐等。这些方法在一定程度上缓
吴恩达深度学习笔记(30)-正则化的解释极客Array
正则化（Regularization）深度学习可能存在过拟合问题——高方差，有两个解决方法，一个是正则化，另一个是准备更多的数据，这是非常可靠的方法，但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高，但正则化通常有助于避免过拟合或减少你的网络误差。如果你怀疑神经网络过度拟合了数据，即存在高方差问题，那么最先想到的方法可能是正则化，另一个解决高方差的方法就是准备更多数据，这也是非常
个人学习笔记7-6：动手学深度学习pytorch版-李沐浪子L 深度学习深度学习笔记计算机视觉 python 人工智能神经网络 pytorch
#人工智能##深度学习##语义分割##计算机视觉##神经网络#计算机视觉13.11全卷积网络全卷积网络（fullyconvolutionalnetwork，FCN）采用卷积神经网络实现了从图像像素到像素类别的变换。引入l转置卷积（transposedconvolution）实现的，输出的类别预测与输入图像在像素级别上具有一一对应关系：通道维的输出即该位置对应像素的类别预测。13.11.1构造模型下
深度学习-点击率预估-研究论文2024-09-14速读 sp_fyf_2024 深度学习人工智能
深度学习-点击率预估-研究论文2024-09-14速读1.DeepTargetSessionInterestNetworkforClick-ThroughRatePredictionHZhong,JMa,XDuan,SGu,JYao-2024InternationalJointConferenceonNeuralNetworks,2024深度目标会话兴趣网络用于点击率预测摘要：这篇文章提出了一种新
损失函数与反向传播 Star_. PyTorch pytorch 深度学习 python
损失函数定义与作用损失函数(lossfunction)在深度学习领域是用来计算搭建模型预测的输出值和真实值之间的误差。1.损失函数越小越好2.计算实际输出与目标之间的差距3.为更新输出提供依据（反向传播)常见的损失函数回归常见的损失函数有：均方差（MeanSquaredError，MSE）、平均绝对误差（MeanAbsoluteErrorLoss，MAE）、HuberLoss是一种将MSE与MAE
【深度学习】训练过程中一个OOM的问题，太难查了 weixin_40293999 深度学习深度学习人工智能
现象：各位大佬又遇到过ubuntu的这个问题么？现象是在训练过程中，ssh上不去了，能ping通，没死机，但是ubunutu的pc侧的显示器，鼠标啥都不好用了。只能重启。问题原因：OOM了95G，尼玛！！！！pytorch爆内存了，然后journald假死了，在journald被watchdog干掉之后，系统就崩溃了。这种规模的爆内存一般，即使被oomkill了，也要卡半天的，确实会这样，能不能配
探索未来，大规模分布式深度强化学习——深入解析IMPALA架构汤萌妮Margaret
探索未来，大规模分布式深度强化学习——深入解析IMPALA架构scalable_agent项目地址:https://gitcode.com/gh_mirrors/sc/scalable_agent在当今的人工智能研究前沿，深度强化学习（DRL）因其在复杂任务中的卓越表现而备受瞩目。本文要介绍的是一个开源于GitHub的重量级项目：“ScalableDistributedDeep-RLwithImp
云服务业界动态简报-20180128 Captain7
一、青云青云QingCloud推出深度学习平台DeepLearningonQingCloud，包含了主流的深度学习框架及数据科学工具包，通过QingCloudAppCenter一键部署交付，可以让算法工程师和数据科学家快速构建深度学习开发环境，将更多的精力放在模型和算法调优。二、腾讯云1.腾讯云正式发布腾讯专有云TCE(TencentCloudEnterprise)矩阵，涵盖企业版、大数据版、AI
机器学习VS深度学习 nfgo 机器学习
机器学习（MachineLearning,ML）和深度学习（DeepLearning,DL）是人工智能（AI）的两个子领域，它们有许多相似之处，但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分：1.概念层面机器学习：是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习，常用的模型有决策树、支持向量机、线性回归等。深度学习：是机器学习的一个子领
ResNet的半监督和半弱监督模型 Valar_Morghulis
Billion-scalesemi-supervisedlearningforimageclassificationhttps://arxiv.org/pdf/1905.00546.pdfhttps://github.com/facebookresearch/semi-supervised-ImageNet1K-models/权重在timm中也有：https://hub.fastgit.org/r
联邦学习 Federated learning Google I/O‘19 笔记努力搬砖的星期五笔记联邦学习机器学习机器学习 tensorflow
FederatedLearning:MachineLearningonDecentralizeddatahttps://www.youtube.com/watch?v=89BGjQYA0uE文章目录FederatedLearning:MachineLearningonDecentralizeddata1.DecentralizeddataEdgedevicesGboard:mobilekeyboa
PCL 怎样可视化深度图像 LeonDL168 PCL 计算机视觉人工智能视觉检测图像处理算法
本小节讲解如何可视化深度图像的两种方法，在3D视窗中以点云形式进行可视化（深度图像来源于点云），另一种是，将深度值映射为颜色，从而以彩色图像方式可视化深度图像。代码首先，在PCL（PointCloudLearning）中国协助发行的书提供光盘的第7章例2文件夹中，打开名为range_image_visualization.cpp的代码文件，同文件夹下可以找到相关的测试点云文件room_scan1.
大数据毕业设计hadoop+spark+hive知识图谱租房数据分析可视化大屏租房推荐系统 58同城租房爬虫房源推荐系统房价预测系统计算机毕业设计机器学习深度学习人工智能 2401_84572577 程序员大数据 hadoop 人工智能
做了那么多年开发，自学了很多门编程语言，我很明白学习资源对于学一门新语言的重要性，这些年也收藏了不少的Python干货，对我来说这些东西确实已经用不到了，但对于准备自学Python的人来说，或许它就是一个宝藏，可以给你省去很多的时间和精力。别在网上瞎学了，我最近也做了一些资源的更新，只要你是我的粉丝，这期福利你都可拿走。我先来介绍一下这些东西怎么用，文末抱走。（1）Python所有方向的学习路线（
深度学习-13-小语言模型之SmolLM的使用皮皮冰燃深度学习深度学习
文章附录1SmolLM概述1.1SmolLM简介1.2下载模型2运行2.1在CPU/GPU/多GPU上运行模型2.2使用torch.bfloat162.3通过位和字节的量化版本3应用示例4问题及解决4.1attention_mask和pad_token_id报错4.2max_new_tokens=205参考附录1SmolLM概述1.1SmolLM简介SmolLM是一系列尖端小型语言模型，提供三种规
基于深度学习的农作物病害检测 SEU-WYL 深度学习dnn 深度学习人工智能
基于深度学习的农作物病害检测利用卷积神经网络（CNN）、生成对抗网络（GAN）、Transformer等深度学习技术，自动识别和分类农作物的病害，帮助农业工作者提高作物管理效率、减少损失。1.农作物病害检测的挑战病害种类繁多：农作物病害的类型多样，不同病害在同一作物上的表现差异很大，同时同一种病害在不同生长阶段的症状也可能不同。环境影响：天气、光照、湿度等外部环境因素会影响农作物的表现，使得病害检
基于深度学习的文本引导的图像编辑 SEU-WYL 深度学习dnn 深度学习人工智能
基于深度学习的文本引导的图像编辑（Text-GuidedImageEditing）是一种通过自然语言文本指令对图像进行编辑或修改的技术。它结合了图像生成和自然语言处理（NLP）的最新进展，使用户能够通过描述性文本对图像内容进行精确的调整和操控。1.文本引导的图像编辑的挑战文本和图像之间的对齐：如何将文本中的语义信息准确地映射到图像中的特定区域或元素是一个关键挑战。这涉及到多模态数据的对齐和理解。编
深度学习--对抗生成网络（GAN, Generative Adversarial Network） Ambition_LAO 深度学习生成对抗网络
对抗生成网络（GAN,GenerativeAdversarialNetwork）是一种深度学习模型，由IanGoodfellow等人在2014年提出。GAN主要用于生成数据，通过两个神经网络相互对抗，来生成以假乱真的新数据。以下是对GAN的详细阐述，包括其概念、作用、核心要点、实现过程、代码实现和适用场景。1.概念GAN由两个神经网络组成：生成器（Generator）和判别器（Discrimina
深度学习：怎么看pth文件的参数奥利给少年深度学习人工智能
.pth文件是PyTorch模型的权重文件，它通常包含了训练好的模型的参数。要查看或使用这个文件，你可以按照以下步骤操作：1.确保你有模型的定义你需要有创建这个.pth文件时所用的模型的代码。这意味着你需要有模型的类定义和架构。2.加载模型权重使用PyTorch的load_state_dict方法来加载权重。这里是如何操作的：importtorchimporttorch.nnasnn#定义模型结构
chatgpt赋能python：如何在Python中安装Keras库？ turensu ChatGpt python chatgpt keras 计算机
如何在Python中安装Keras库？Keras是一个简单易用的神经网络库，由FrançoisChollet编写。它在Python编程语言中实现了深度学习的功能，可以使您更轻松地构建和试验不同类型的神经网络。如果您是一名Python开发人员，肯定会想知道如何在您的Python项目中安装Keras库。在本文中，我们将向您展示如何安装和配置Keras库。步骤1：安装Python要使用Keras库，您需
如何理解深度学习的训练过程奋斗的草莓熊深度学习人工智能 python scikit-learn virtualenv numpy pandas
文章目录1.训练是干什么？2.预训练模型进行训练，主要更改的是预训练模型的什么东西？1.训练是干什么？以yolov5为例子，训练的目的是把一组输入猫狗图像放到神经网络中，得到一个输出模型，这个模型下次可以直接用来识别哪个是猫，哪个是狗2.预训练模型进行训练，主要更改的是预训练模型的什么东西？超参数（Hyperparameters）：这是模型结构中定义的参数，比如：卷积核大小（kernel_size
Keras深度学习框架入门及实战指南司莹嫣Maude
Keras深度学习框架入门及实战指南keraskeras-team/keras:是一个基于Python的深度学习库，它没有使用数据库。适合用于深度学习任务的开发和实现，特别是对于需要使用Python深度学习库的场景。特点是深度学习库、Python、无数据库。项目地址:https://gitcode.com/gh_mirrors/ke/keras一、项目介绍Keras简介Keras是一款高级神经网络
深度学习驱动的车牌识别：技术演进与未来挑战逼子歌深度学习车牌识别神经网络字符识别 YOLO 卷积神经网络
一、引言1.1研究背景在当今社会，智能交通系统的发展日益重要，而车牌识别作为其关键组成部分，发挥着至关重要的作用。车牌识别技术广泛应用于交通管理、停车场管理、安防监控等领域。在交通管理中，它可以用于车辆识别、交通违法监控和车流统计等，提高交通管理的效率和准确性。在停车场管理中，实现车辆的自动识别和收费，提升管理和服务水平。在安防监控领域，可用于追踪嫌疑人及犯罪行为。深度学习的出现为车牌识别带来了重
Hadoop(一) 朱辉辉33 hadoop linux
今天在诺基亚第一天开始培训大数据，因为之前没接触过Linux，所以这次一起学了，任务量还是蛮大的。首先下载安装了Xshell软件，然后公司给了账号密码连接上了河南郑州那边的服务器，接下来开始按照给的资料学习，全英文的，头也不讲解，说锻炼我们的学习能力，然后就开始跌跌撞撞的自学。这里写部分已经运行成功的代码吧. 在hdfs下，运行hadoop fs -mkdir /u
maven An error occurred while filtering resources blackproof maven 报错
转：http://stackoverflow.com/questions/18145774/eclipse-an-error-occurred-while-filtering-resources maven报错： maven An error occurred while filtering resources Maven -> Update Proje
jdk常用故障排查命令 daysinsun jvm
linux下常见定位命令： 1、jps 输出Java进程 -q 只输出进程ID的名称，省略主类的名称； -m 输出进程启动时传递给main函数的参数； &nb
java 位移运算与乘法运算周凡杨 java 位移运算乘法
对于 JAVA 编程中，适当的采用位移运算，会减少代码的运行时间，提高项目的运行效率。这个可以从一道面试题说起：问题：用最有效率的方法算出2 乘以8 等於几?” 答案：2 << 3 由此就引发了我的思考，为什么位移运算会比乘法运算更快呢？其实简单的想想，计算机的内存是用由 0 和 1 组成的二
java中的枚举(enmu) g21121 java
从jdk1.5开始，java增加了enum(枚举)这个类型，但是大家在平时运用中还是比较少用到枚举的，而且很多人和我一样对枚举一知半解，下面就跟大家一起学习下enmu枚举。先看一个最简单的枚举类型，一个返回类型的枚举： public enum ResultType { /** * 成功 */ SUCCESS, /** * 失败 */ FAIL,
MQ初级学习 510888780 activemq
1.下载ActiveMQ 去官方网站下载：http://activemq.apache.org/ 2.运行ActiveMQ 解压缩apache-activemq-5.9.0-bin.zip到C盘，然后双击apache-activemq-5.9.0-\bin\activemq-admin.bat运行ActiveMQ程序。启动ActiveMQ以后，登陆：http://localhos
Spring_Transactional_Propagation 布衣凌宇 spring transactional
//事务传播属性 @Transactional(propagation=Propagation.REQUIRED)//如果有事务，那么加入事务，没有的话新创建一个 @Transactional(propagation=Propagation.NOT_SUPPORTED)//这个方法不开启事务 @Transactional(propagation=Propagation.REQUIREDS_N
我的spring学习笔记12-idref与ref的区别 aijuans spring
idref用来将容器内其他bean的id传给<constructor-arg>/<property>元素，同时提供错误验证功能。例如： <bean id ="theTargetBean" class="..." /> <bean id ="theClientBean" class=&quo
Jqplot之折线图 antlove js jquery Web timeseries jqplot
timeseriesChart.html <script type="text/javascript" src="jslib/jquery.min.js"></script> <script type="text/javascript" src="jslib/excanvas.min.js&
JDBC中事务处理应用百合不是茶 java JDBC编程事务控制语句
解释事务的概念; 事务控制是sql语句中的核心之一;事务控制的作用就是保证数据的正常执行与异常之后可以恢复事务常用命令: Commit提交
[转]ConcurrentHashMap Collections.synchronizedMap和Hashtable讨论 bijian1013 java 多线程线程安全 HashMap
在Java类库中出现的第一个关联的集合类是Hashtable，它是JDK1.0的一部分。 Hashtable提供了一种易于使用的、线程安全的、关联的map功能，这当然也是方便的。然而，线程安全性是凭代价换来的――Hashtable的所有方法都是同步的。此时，无竞争的同步会导致可观的性能代价。Hashtable的后继者HashMap是作为JDK1.2中的集合框架的一部分出现的，它通过提供一个不同步的
ng-if与ng-show、ng-hide指令的区别和注意事项 bijian1013 JavaScript AngularJS
angularJS中的ng-show、ng-hide、ng-if指令都可以用来控制dom元素的显示或隐藏。ng-show和ng-hide根据所给表达式的值来显示或隐藏HTML元素。当赋值给ng-show指令的值为false时元素会被隐藏，值为true时元素会显示。ng-hide功能类似，使用方式相反。元素的显示或
【持久化框架MyBatis3七】MyBatis3定义typeHandler bit1129 TypeHandler
什么是typeHandler? typeHandler用于将某个类型的数据映射到表的某一列上，以完成MyBatis列跟某个属性的映射内置typeHandler MyBatis内置了很多typeHandler，这写typeHandler通过org.apache.ibatis.type.TypeHandlerRegistry进行注册，比如对于日期型数据的typeHandler，
上传下载文件rz,sz命令 bitcarter linux命令rz
刚开始使用rz上传和sz下载命令：因为我们是通过secureCRT终端工具进行使用的所以会有上传下载这样的需求：我遇到的问题： sz下载A文件10M左右，没有问题但是将这个文件A再传到另一天服务器上时就出现传不上去，甚至出现乱码，死掉现象，具体问题解决方法：上传命令改为;rz -ybe 下载命令改为：sz -be filename 如果还是有问题：那就是文
通过ngx-lua来统计nginx上的虚拟主机性能数据 ronin47 ngx-lua　统计解禁ip
介绍以前我们为nginx做统计,都是通过对日志的分析来完成.比较麻烦,现在基于ngx_lua插件,开发了实时统计站点状态的脚本,解放生产力.项目主页: https://github.com/skyeydemon/ngx-lua-stats 功能支持分不同虚拟主机统计, 同一个虚拟主机下可以分不同的location统计. 可以统计与query-times request-time
java-68-把数组排成最小的数。一个正整数数组，将它们连接起来排成一个数，输出能排出的所有数字中最小的。例如输入数组{32, 321}，则输出32132 bylijinnan java
import java.util.Arrays; import java.util.Comparator; public class MinNumFromIntArray { /** * Q68输入一个正整数数组，将它们连接起来排成一个数，输出能排出的所有数字中最小的一个。 * 例如输入数组{32, 321}，则输出这两个能排成的最小数字32132。请给出解决问题
Oracle基本操作 ccii Oracle SQL总结 Oracle SQL语法 Oracle基本操作 Oracle SQL
一、表操作 1. 常用数据类型 NUMBER(p,s)：可变长度的数字。p表示整数加小数的最大位数，s为最大小数位数。支持最大精度为38位 NVARCHAR2(size)：变长字符串，最大长度为4000字节（以字符数为单位） VARCHAR2(size)：变长字符串，最大长度为4000字节（以字节数为单位） CHAR(size)：定长字符串，最大长度为2000字节，最小为1字节，默认
[强人工智能]实现强人工智能的路线图 comsci 人工智能
1：创建一个用于记录拓扑网络连接的矩阵数据表 2:自动构造或者人工复制一个包含10万个连接(1000*1000)的流程图 3：将这个流程图导入到矩阵数据表中 4：在矩阵的每个有意义的节点中嵌入一段简单的
给Tomcat，Apache配置gzip压缩(HTTP压缩)功能 cwqcwqmax9 apache
背景： HTTP 压缩可以大大提高浏览网站的速度，它的原理是，在客户端请求网页后，从服务器端将网页文件压缩，再下载到客户端，由客户端的浏览器负责解压缩并浏览。相对于普通的浏览过程HTML ,CSS,Javascript , Text ，它可以节省40%左右的流量。更为重要的是，它可以对动态生成的，包括CGI、PHP , JSP , ASP , Servlet,SHTML等输出的网页也能进行压缩，
SpringMVC and Struts2 dashuaifu struts2 springMVC
SpringMVC VS Struts2 1: spring3开发效率高于struts 2: spring3 mvc可以认为已经100%零配置 3: struts2是类级别的拦截，一个类对应一个request上下文， springmvc是方法级别的拦截，一个方法对应一个request上下文，而方法同时又跟一个url对应所以说从架构本身上 spring3 mvc就容易实现r
windows常用命令行命令 dcj3sjt126com windows cmd command
在windows系统中，点击开始－运行，可以直接输入命令行，快速打开一些原本需要多次点击图标才能打开的界面，如常用的输入cmd打开dos命令行，输入taskmgr打开任务管理器。此处列出了网上搜集到的一些常用命令。winver 检查windows版本 wmimgmt.msc 打开windows管理体系结构(wmi) wupdmgr windows更新程序 wscrip
再看知名应用背后的第三方开源项目 dcj3sjt126com ios
知名应用程序的设计和技术一直都是开发者需要学习的，同样这些应用所使用的开源框架也是不可忽视的一部分。此前《 iOS第三方开源库的吐槽和备忘》中作者ibireme列举了国内多款知名应用所使用的开源框架，并对其中一些框架进行了分析，同样国外开发者 @iOSCowboy也在博客中给我们列出了国外多款知名应用使用的开源框架。另外txx's blog中详细介绍了 Facebook Paper使用的第三
Objective-c单例模式的正确写法 jsntghf 单例 ios iPhone
一般情况下，可能我们写的单例模式是这样的： #import <Foundation/Foundation.h> @interface Downloader : NSObject + (instancetype)sharedDownloader; @end #import "Downloader.h" @implementation
jquery easyui datagrid 加载成功，选中某一行 hae jquery easyui datagrid 数据加载
1.首先你需要设置datagrid的onLoadSuccess $( '#dg' ).datagrid({onLoadSuccess : function (data){ $( '#dg' ).datagrid( 'selectRow' ,3); }}); 2.onL
jQuery用户数字打分评价效果 ini JavaScript html jquery Web css
效果体验：http://hovertree.com/texiao/jquery/5.htmHTML文件代码： <!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"> <head> <title>jQuery用户数字打分评分代码 - HoverTree</
mybatis的paramType kerryg DAO sql
MyBatis传多个参数： 1、采用#{0},#{1}获得参数： Dao层函数方法： public User selectUser(String name,String area); 对应的Mapper.xml <select id="selectUser" result
centos 7安装mysql5.5 MrLee23 centos
首先centos7 已经不支持mysql，因为收费了你懂得，所以内部集成了mariadb，而安装mysql的话会和mariadb的文件冲突，所以需要先卸载掉mariadb，以下为卸载mariadb，安装mysql的步骤。 #列出所有被安装的rpm package rpm -qa | grep mariadb #卸载 rpm -e mariadb-libs-5.
利用thrift来实现消息群发 qifeifei thrift
Thrift项目一般用来做内部项目接偶用的，还有能跨不同语言的功能，非常方便，一般前端系统和后台server线上都是3个节点，然后前端通过获取client来访问后台server，那么如果是多太server，就是有一个负载均衡的方法，然后最后访问其中一个节点。那么换个思路，能不能发送给所有节点的server呢，如果能就
实现一个sizeof获取Java对象大小 teasp java HotSpot 内存对象大小 sizeof
由于Java的设计者不想让程序员管理和了解内存的使用，我们想要知道一个对象在内存中的大小变得比较困难了。本文提供了可以获取对象的大小的方法，但是由于各个虚拟机在内存使用上可能存在不同，因此该方法不能在各虚拟机上都适用，而是仅在hotspot 32位虚拟机上，或者其它内存管理方式与hotspot 32位虚拟机相同的虚拟机上适用。
SVN错误及处理 xiangqian0505 SVN提交文件时服务器强行关闭
在SVN服务控制台打开资源库“SVN无法读取current” ---摘自网络写道 SVN无法读取current修复方法 Can't read file : End of file found 文件：repository/db/txn_current、repository/db/current 其中current记录当前最新版本号，txn_current记录版本库中版本

MyDLNote - Attention: ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks

MyDLNote - Attention: [2020CVPR] ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks

Abstract

Introduction

Proposed Method

Revisiting Channel Attention in SE Block

Efficient Channel Attention (ECA) Module

Coverage of Local Cross-Channel Interaction

ECA Module for Deep CNNs

Code

你可能感兴趣的:(deep,learning,深度学习)