彩色分割--数字图像处理作业
简答题
从下面任选一图,分割出图中的鱼、花或蝴蝶。(需包含所用算法原理 、处理步骤、结果图片及关键代码)
答案
1. 选题。选择向日葵图片进行分割。
2. 思路。图片背景是蓝色的天空,考虑对蓝色部分分割出来后,在原图基础上减去分割所得图像即可达到向日葵。
3. 算法原理。在RGB空间上使用基于曼哈顿距离的分割算法。
1. 曼哈顿距离。基于曼哈顿距离的优势在于,相较于欧式距离,它的计算量大大减少,其核心思想是在边界盒中心α 处,沿每一个颜色轴选择的维数与沿每个轴的样本的标准差成比例,标准差的计算只使用一次样本颜色数据。
2. 基于曼哈顿距离的彩色分割算法原理。通过采样可以确定欲分割区域的彩色平均向量α,选定边界盒各通道的范围之后,将各通道颜色位于边界范围内的像素点提取出来,便完成了分割。被分割像素需满足的色彩标准为:
![]()
其中η是阈值系数,σ是各通道的标准差
4. 步骤。
step1. 读取图像,划出要去除的(或分割)的区域
step2. 计算各通道的平均曼哈顿距离,(使用单通道曼哈顿法只计算要去除那个通道就行)
step3. 调整各通道对应的标准差的比例系数,作为阈值,对同时满足三个阈值限制的像素位置记1否则记0,进一步得到二值图.(单通道法计算单个通道)
step4. 原图与二值图对应元素相乘,便得到了分割后的图像
5. 代码
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = 'sunflower.jpg'
f_bgr = cv2.imread(img, cv2.IMREAD_COLOR)
f_rgb = cv2.cvtColor(f_bgr, cv2.COLOR_BGR2RGB)
#确定要分割出来的颜色的区域
bndbox = {'xmin': 380,'ymin': 200,'xmax': 474,'ymax': 300}
f_rec = cv2.rectangle(f_rgb.copy(),
(bndbox['xmin'], bndbox['ymin']),
(bndbox['xmax'], bndbox['ymax']),
color=(255, 255, 0), thickness=3)
cv2.imwrite("bndbox.jpg",f_rec)
plt.imshow(f_rec)
plt.savefig("bndbox")
plt.show()
def binary_mix(f, b):
"""
混合输入图像和二值化图像,相当于图像的与操作
:参数 f: 输入图像
:参数 b: 二值图像
"""
g = f.copy()
H, W, C = g.shape
#遍历每个通道的每个像素,与对应二值相乘
for c in range(C):
g[:, :, c] = np.multiply(g[:, :, c], b)
return g
def single_Manhattan(f, box, eta, channel=0):
"""
计算单通道平均曼哈顿距离并返回二值化图像
:参数 f: img
:参数 box: 选择的分割的区域
:参数 eta: 阈值系数
:参数 channel: 通道索引
"""
H, W, C = f.shape #读取图像维度
b = np.zeros((H, W), dtype='int') #设置空矩阵
c = f[box[0]:box[2], box[1]:box[3] , channel] #取出框出的部分该通道的数值
a = np.mean(c) #求该通道灰度平均值
sigma = np.std(c) #求该通道灰度标准差
#遍历整幅图像的对应通道,对满足色彩条件的记1,形成二值图像
for w in range(W):
for h in range(H):
z = f[h, w, channel]
if np.abs(z - a) <= eta * sigma:
b[h, w] = 1
return b
def multi_weight_Manhattan(f, box, etas):
"""
计算多通道平均曼哈顿距离并返回二值化图像
:参数 f: img
:参数 box: 选择的分割的区域
:参数 eta: 阈值系数
:参数 channel: 通道索引
"""
H, W, C = f.shape
bs = np.zeros_like(f, dtype='int') # bs 是图像每个通道的有效二值化矩阵
#先求每个通道的二值化图像
for c in range(C):
bs[:, :, c] = single_Manhattan(f, box, etas[c], c)
b = np.sum(bs, axis=2) #三张二值图像对应位置求和
for w in range(W):
for h in range(H):
if b[h, w] == C: #当三个条件都满足时,该值为3,此时可以记1,从而得到整个图的二值图
temp = 1
else:
temp = 0
b[h, w] = temp
return b
#开始分割
fig, axs = plt.subplots(1, 3, figsize=(10, 4))
#各通道灰度图
axs[0].set_title('R')
axs[0].imshow(f_rgb[:, :, 0], cmap='gray')
axs[1].set_title('G')
axs[1].imshow(f_rgb[:, :, 1], cmap='gray')
axs[2].set_title('B')
axs[2].imshow(f_rgb[:, :, 2], cmap='gray')
plt.suptitle('RGB')
plt.savefig("rgb_gray")
plt.show()
# 多通道带权重的的平均曼哈顿距离
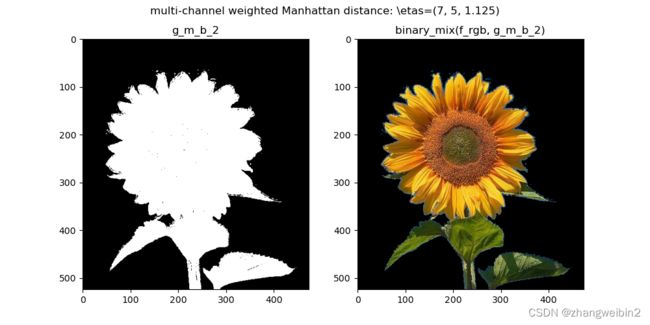
eta2 = (7, 5, 1.125) #设置阈值系数
g_m_b_2 = multi_weight_Manhattan(f_rgb, list(bndbox.values()), etas=eta2)
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
axs[0].set_title('g_m_b_2')
axs[0].imshow(g_m_b_2, cmap='gray')
axs[1].set_title('binary_mix(f_rgb, g_m_b_2)')
axs[1].imshow(binary_mix(f_rgb, g_m_b_2))
plt.suptitle(r'multi-channel weighted Manhattan distance: \etas={}'.format(str(eta2)))
plt.savefig('result')
plt.show()6. 实验结果及分析
图1所示,选择颜色过渡的地方作为取色区域,计算该区域的均值,标准差。由图2可见,欲分割部分,R通道灰度值较高,G通道灰度值适中,B通道灰度值很小。于是大致上,依照R通道阈值放较宽、G通道阈值小一点、B通道阈值设置较小的原则调整阈值系数,最终得到图3的分割效果。