《信息检索导论》第五章总结
一、索引压缩概述
使用压缩的目的:
(1)因为我们想要把尽量多的数据放入内存,因此压缩能够达到这个目的;
(2)从磁盘到内存的传输时间会缩短;
压缩分类:
(1)无损压缩:压缩后的数据能还原全部信息;
(2)有损压缩:压缩后会丢失一些信息;
如果有损压缩后丢失的信息用户并不关心,则有损压缩也是可以接受的;
二、Heaps定律
通过整个文档集词条数来估计词项数目;
主要思想:随着文档集增加,词项数目会增加,并且没有上限;
M=kT^b;
三、Zipf定律
通过词项在文档集中的词频排名来估计词项之间的词频比例;
如果词项A出现次数排名第一,词项B出现次数排名第二,词项C出现次数排名第三,则A出现次数是B出现次数的两倍,则A出现次数是C出现次数的1/3;
四、词典压缩
虽然与倒排记录表相比,词典的空间很小,但是为了能够把词典全部都放在内存中,我们必须要对其进行压缩;
1.词项定长存储
固定词项分配大小为20B;
需要空间:M*(20+4+4)=M*28;
缺点:
(1)大部分单词都少于20B,浪费空间;
(2)对于某几个大于20B的单词也不能存储;
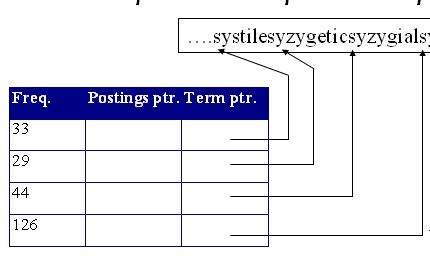
2.词项作为一个字符串
将每个词项合并,并组成一个长字符串;
对于每个词项增加一个指针;
需要空间:M*(8+4+4+3)=M*19;
相比之前,减少了1/3;
3.按块存储
将词典分组,分成n块,并且只有每个块的第一个词项有指针指向长字符串;
在长字符串的每个词项前面添加一个词项长度;
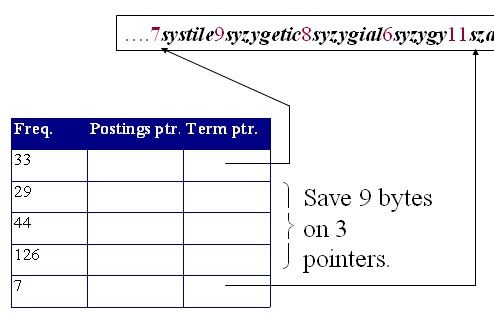
如果每个块大小为4,则每个块可以减少3个指针,加上4个字节表示4个词项的长度;
因此需要空间:M(4+4+8)+M/4*3-M=M(16-1/4);
相比之前又减少了15M/4;
但是每个块越大,压缩率越大,则查询的时间就越长;
因为一开始先通过二分搜索查找到词项所在块的入口,然后线性搜索找到词项;
二叉树高度计算方法:
已知n个结点,这些节点构成的二叉树的高度为:
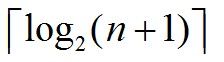
如果给定高度为n,则满二叉树的节点个数为
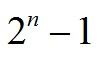
4.前端编码
对于3的改进方法是对于长字符串的编排进行改进;
我们可以提取公共前缀;
比如原来8automate9automatic,可以变成automat*1e.2ic;
此方法能够减少存储空间;
五、posting压缩
一般来说词项出现频率高,则posting连续两个docID不会相差(gap)太远,比如:
the ---> 10000 10001 10002;
如果我们通过记录两docID的间距,则会大大减少存储的空间;
the ---> 10000 1 1;
压缩率越高,解压缩时间就越长;
1.VB编码
规则:
(1)编码结果是整数个字节;
(2)每个字节的第一位是延续位,如果为1,则表示是最后一个字节,否则,则表示不是最后一个字节;
(3)每个字节的其他7位为正常编码位;
举例:
3 ---> 1 0000011;
注意:可变字节编码的解码消耗比起可变位编码消耗要低得多;
一个字节用VB编码的最大间距是127;2^7-1;因为如果需要编码,则说明此数肯定不是0,因此从1开始;
2.一元编码
如果为数n,则n个1后面添一个0;
举例:5 ---> 111110
3.gamma编码
规则:
(1)不记录最高位的1;比如12 ---> 100;
(2)编码分为长度和偏移(长度指的是偏移的长度)
(3)长度采用一元编码,根据偏移的长度进行编码;
(4)偏移采用(1)的编码;
举例:12 ---> 1110(长度),100(偏移);
编码长度:2log(G)+1;
总结:gamma编码能够压缩成原始posting的1/4,即如果原来posting为400M,则现在gamma编码后只需要100M即可;
注意:
(1)gamma编码永远是基数位;
(2)前缀无关即解码结果唯一性;
4.最优编码长度
如果数G,则最优编码为log(G);
举例:如果为12,则最优编码为4;
5.Universal code
和最优编码长度只相差常数个倍数的编码方式,gamma就是一个universal code;