西瓜书第一章绪论

先放上参考和转载部分程序的链接：
https://blog.csdn.net/u014134327/article/details/94397454
https://blog.csdn.net/weixin_42702793/article/details/104178807
https://blog.csdn.net/dicker6315/article/details/81265066

以上都是我学习过程中看到的很好的文章，感谢他们对我的帮助！

---

前言

为了更好地迎接研究生阶段的到来，准备在大四学年提前完善自己在机器学习方面的知识体系。在西瓜书里有很多数学公式的推导和课后的习题，在学习过程中需要不断记录，希望小菜鸡我可以坚持下来。
由于我能力还比较弱，就想做一个记录的形式，所以在这个过程中可能有的部分会引用一些其他人的程序和思路，但我都会在一开始注明来源，如果说有遗漏的或者弄错了来源，麻烦看到的大家提醒我一下下！

---

内容：公式推导、习题理解

一、公式推导

第一章里面的“没有免费的午餐”定理（No Free Lunch Theorem,NFL），我主要记录一下我起初没有很看懂的地方，然后展开推导一下。
在式（1.2）的第2行推导至第3行的过程中，有一处是这样的：

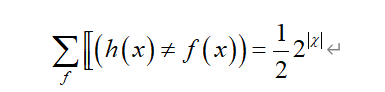
举个例子来理解，假设样本空间有3个样本时，X={x1,x2,x3}（就是样本空间，也就是上面式子里2的次方绝对值里面的东西，但我还不会用csdn敲符号，所以就写成X，但是事实上在这个证明里面X另有所指哈，还是要严谨），|X|=3，那么所有真实目标函数f有如下几种可能：
（1）f1: f1(x1)=0, f1(x2)=0, f1(x3)=0;
（2）f2: f2(x1)=0, f2(x2)=0, f2(x3)=1;
（3）f3: f3(x1)=0, f3(x2)=1, f3(x3)=0;
（4）f4: f4(x1)=0, f4(x2)=1, f4(x3)=1;
（5）f5: f5(x1)=1, f5(x2)=0, f5(x3)=0;
（6）f6: f6(x1)=1, f6(x2)=0, f6(x3)=1;
（7）f7: f7(x1)=1, f7(x2)=1, f7(x3)=0;
（8）f8: f8(x1)=1, f8(x2)=1, f8(x3)=1;
也就是有2^|X|=2³=8个可能的真实目标函数。
那么，也就意味着由算法学习出来的模型h(x)对每个样本的预测值无论是0还是1，都一定会有一半数量的可能真实目标函数与之预测值相同。比如说，h(x)对x1的预测值是1，那么只有f5、f6、f7和f8满足与h(x)的预测值一致。

二、习题理解

1.1

1、（色泽=青绿；根蒂=蜷缩；敲声=浊响）
2、（色泽=ALL；根蒂=蜷缩；敲声=浊响）
3、（色泽=青绿；根蒂=ALL；敲声=浊响）
4、（色泽=青绿；根蒂=蜷缩；敲声=ALL）
5、（色泽=青绿；根蒂=ALL；敲声=ALL）
6、（色泽=ALL；根蒂=蜷缩；敲声=ALL）
7、（色泽=ALL；根蒂=ALL；敲声=浊响）

为了便于理解，形成代码如下：

//代码参考来源：https://blog.csdn.net/u014134327/article/details/94397454
color = {0: '01', 1: '10', 2: '11'}
root = {0: '01', 1: '10', 2: '11'}
sound = {0: '01', 1: '10', 2: '11'}

good = 0b010101
bad = 0b101010

space = []

for i in range(3):
    for j in range(3):
        for k in range(3):
            tempStr = '0b' + color[i] + root[j] + sound[k]
            tempInt = int(tempStr, 2)
            if tempInt | good == tempInt and tempInt | bad != tempInt:
                space.append(bin(tempInt))

print(space)

1.2

首先感谢这篇写的超级无敌清楚的博客：https://blog.csdn.net/weixin_42702793/article/details/104178807
接下来，我就再按照自己的理解重述一下下

第一步，先来解决题目中关于“k个合取式的析合范式”怎么理解的问题。
通过参考上面的博客，我想这种方式是比较直观并且好理解的，就是将每一个好瓜的特征描述用一个数字表示，比如说：（色泽=青绿；根蒂=蜷缩；敲声=浊响）表示为1，（色泽=乌黑；根蒂=蜷缩；敲声=浊响）表示为2，诸如此类。
对于本道题中的数据，可以知道瓜的三种特性分别有如下取值情况：
（1）色泽：青绿、乌黑
（2）根蒂：蜷缩、硬挺、稍蜷
（3）敲声：浊响、清脆、沉闷
所以说，也就一共有2X3X3=18种组合。
于是我们就把这18种情况简化成一个集合:
S=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]

第二步，我们来讨论k在不同取值下的假设空间。
（1）当k=1时，共有18个析合范式，如下:[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]

（2）当k=2时，共有153个析合范式，如下：
[(1,2),(1,3),(1,4),…,(1,18),(2,3),(2,4),…,(2,18),(3,4),(3,5),…,(17,18)]

Attention：这里有一个小问题，就是为什么没有(1,1)，(2,1)之类的呢？那是因为(1,1)与1是等价的（k取其他值也是一样的），而(2,1)与(1,2)也是等价的呀，所以就会出现了冗余的问题，因此这些都是没有必要的！！

（3）当k=3时，共有816个析合范式，如下：
[(1,2,3),(1,2,4),…(1,3,4),…]
形成代码如下：

//代码参考来源：https://blog.csdn.net/weixin_42702793/article/details/104178807
result=0
for i in range(1,17):
    for j in range((i+1),19):
        for k in range((j+1),19):
            print((i,j,k))
            result=result+1
print(result)

所以综上所述，k取其他值的时候也可以一样分析出结果啦
下面列出一下k各取值情况下的假设个数：
k=0是，result=1
k=1时，result=18
k=2时，result=153
k=3时，result=816
k=4时，result=3060
k=5时，result=8568
k=6时，result=18564
k=7时，result=31824
k=8时，result=43758
k=9时，result=48620
k=10时，result=43758
k=11时，result=31824
k=12时，result=18564
k=13时，result=8568
k=14时，result=3060
k=15时，result=816
k=16时，result=153
k=17时，result=18
k=18时，result=1

1.3

首先，“数据包含噪声”可以理解为对于训练集的数据，存在一些属性值（attribute value）相同的样本，但是其标记（label）却不同。
那么，在这种情况下，可以选择去除任一类属性值相同但标记不同的数据，比如说两个数据属性值相同，但标记一个positive，一个negative，那么我们可以设计归纳偏好是去除positive的那一类，当然也可以设计成去除negative的那一类。

1.4

这里的证明过程参考了：https://blog.csdn.net/dicker6315/article/details/81265066
此处只放上主体证明部分，引理证明请看上面

1.5

略

---

总结

以上就是第一章的内容，希望能帮助到有需要的人，如果我有表述不当或者错误的地方，也希望大家帮我指正一下，谢谢qwq！