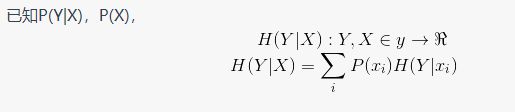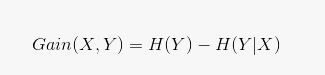机器学习--决策树实验及源码(Python版)
【实验原理】
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称决策树。在机器学习中,决策树是一个预测模型,他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度,使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。
比如说我们想养一只宠物,但是不知道养哪种宠物比较合适。其实我们可以绘制一个决策树,如下图所示:
1、决策树的算法原理
(1)找到划分数据的特征,作为决策点
(2)利用找到的特征对数据进行划分成n个数据子集。
(3)如果同一个子集中的数据属于同一类型就不再划分,如果不属于同一类型,继续利用特征进行划分。
(4)指导每一个子集的数据属于同一类型停止划分。
2、决策树的优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关的特征数据
缺点:可能产生过度匹配的问题
3、那么我们该如何构建一颗决策树呢?在构建一颗决策树的时候我们需要解决的问题有三个:根结点放置哪个条件属性;下面的结点放置哪个属性;什么时候停止树的生长。
为了解决上面三个问题,我们需要引入一些概念。
(1)第一个引入的概念叫信息熵,英文名为 Entropy。在 Tom Mitchell 的书中是这样解释信息熵的:它确定了要编码集合 S 中任意成员(即以均匀的概率随机抽出的一个成员)的分类所需要的最少二进制位数。把它转化成通俗点的语言就是说,信息熵就是“预测随机变量Y的取值”的难度,或者说度量“随机变量Y”的不确定性。
当一个事情非常容易判断的时候,也就是我们以很大的概率认为它会发生或者不会发生,那么它的信息熵就偏向0,当一个事情非常难判断的时候,我们可以认为最难的时候就是这个事件的所有可能性均相等的时候,那么它的信息熵为1。
有很多学者都提出了他们认为的信息熵表达式,我们可以通过下面这个表格看一下目前的一些信息熵的定义。
虽然有这么多的定义,但我们平时很多情况下用的都是香农信息熵。
(2)有了信息熵的概念之后,我们自然而然就可以得出条件信息熵的概念,条件信息熵就是度量“在随机变量X的前提下,预测随机变量Y”的难度。那么条件信息熵的数学表达式就是:
(3)有了信息熵和条件信息熵的概念,那我们就自然而然地就可以引出第三个概念,那就是信息增益,信息增益的数学定义是:
我们通过看这个数学表达式不难看出信息增益所表达的意思。被减数是信息熵,也就是在没人给我们通风报信的时候判断结果的难度;减数是条件信息熵,也就是当我们知道了一个条件后,判断结果的难度。信息增益这个变量表达的意思就是条件x对判断结果减少了多少难度,即度量X对预测Y的能力的影响。
比方说参加问答,当答题选手无法判断答案的时候会选择三种求助方式,其实求助方式就是一种条件,当选手用过了求助方式后对回答问题的难度的减少量,就是信息增益。如果难度降低很大,那么我们就可以说信息增益很大。
【实验环境】
环境一:直接在百度AI Studio上创建一个项目即可。
环境二:
Ubuntu 16.04
Anaconda 4.3
python 3.6
Pycharm(Community)
【实验内容】
本次实验任务我们使用贷款申请样本数据表,该数据表中每列数据分别代表ID、年龄、高薪、有房、信贷情况、类别,我们根据如下数据生成决策树,使用代码来实现该决策树算法。
【实验步骤】
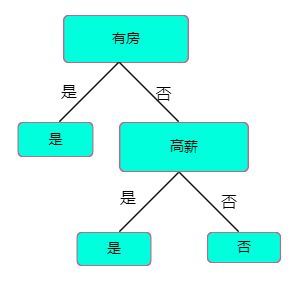
1.构建决策树如下:
该决策树的结构,可以用字典表示为:
{'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
接下来我们编写python代码来递归构建决策树。
# -*- coding: UTF-8 -*-
from math import log
import operator
#计算数据集的香农商
def calcShannonnt(dataSet):
numEntires = len(dataSet) #返回数据集的行数
labelCounts = {} #保存每个标签(Label)出现次数的字典
for featVec in dataSet: #对每组特征向量进行统计
currentLabel = featVec[-1] #提取标签Label的信息
if currentLabel not in labelCounts.keys():
#如果标签label没有放入统计次数的字典,则添加进去
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 #Label计数
shannonEnt = 0.0 #香农熵
for key in labelCounts: #计算香农熵
prob = float(labelCounts[key])/numEntires #选择标签Label的概率
shannonEnt -= prob * log(prob,2) #利用计算公式
return shannonEnt
#创建测试数据集
def testDataset():
dataSet = [[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = ['年龄', '高薪', '有房', '信用情况'] #特征标签
return dataSet, labels
#创建函数splitDataset,按照特征划分数据集。
#axis:划分数据集的特征,value:需要返回的特征值
def splitDataset(dataSet, axis, value):
retDataSet = [] #创建返回的数据集列表
for featVec in dataSet: #遍历数据集
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] #去掉axis特征
reducedFeatVec.extend(featVec[axis+1:]) #将符合条件的添加到返回的数据集中
retDataSet.append(reducedFeatVec)
return retDataSet
#选择最优特征
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #特征数量
baseEntropy = calcShannonent(dataSet) #计算数据集的香农熵
bestInfoGain = 0.0 #信息增益
bestFeature = -1 #最优特征的索引值
for i in range(numFeatures): #遍历所有特征
#获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) #创建set集合{},元素不可重复
newEntropy = 0.0 #经验条件熵
for value in uniqueVals: #计算信息增益
subDataSet = splitDataset(dataSet, i, value) #subDataSet划分后的子集
prob = len(subDataSet) / float(len(dataSet)) #计算子集的概率
newEntropy += prob * calcShannonent(subDataSet) #根据公式计算经验条件熵
infoGain = baseEntropy - newEntropy #信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain)) #打印每个特征的信息增益
if (infoGain > bestInfoGain): #计算信息增益
bestInfoGain = infoGain #更新信息增益,找到最大的信息增益
bestFeature = i #记录信息增益最大的特征的索引值
return bestFeature
#统计classList中出现次数最多的元素(类标签)。
def createTree(dataSet, labels, featLabels):
classList = [example[-1] for example in dataSet] #取分类标签(是否放贷:yes or no)
if classList.count(classList[0]) == len(classList): #如果类别完全相同则停止继续划分
return classList[0]
if len(dataSet[0]) == 1: #遍历完所有特征时返回出现次数最多的类标签
return mostTags(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) #选择最优特征
bestFeatLabel = labels[bestFeat] #最优特征的标签
featLabels.append(bestFeatLabel)
myTree = {bestFeatLabel:{}} #根据最优特征的标签生成树
del(labels[bestFeat]) #删除已经使用特征标签
featValues = [example[bestFeat] for example in dataSet] #得到训练集中所有最优特征的属性值
uniqueVals = set(featValues) #去掉重复的属性值
for value in uniqueVals: #遍历特征,创建决策树。
myTree[bestFeatLabel][value] = createTree(splitDataset(dataSet, bestFeat, value), labels, featLabels)
return myTree
def classify(inputTree,featLabels,testVec):
firstStr=next(iter(inputTree))
secondDict=inputTree[firstStr]
featIndex=featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex]==key:
if type(secondDict[key]).__name__=='dict':
classLabel=classify(secondDict[key],featLabels,testVec)
else:
classLabel=secondDict[key]
return classLabel
if __name__ == '__main__':
dataSet, labels = testDataset()
featLabels = []
myTree = createTree(dataSet, labels, featLabels)
print(myTree)
testVec=[0,1]
result=classify(myTree,featLabels,testVec)
if result=='yes':
print("同意贷款")
if result=='no':
print("拒绝贷款")