2.吴恩达机器学习--逻辑回归
1. 线性可分
根据学生的两门学生成绩,预测该学生是否会被大学录取。数据集 ex2data1.txt 中包含了两门课的成绩以及是否被大学录取,0代表未录取,1代表录取。
1. 导入库,加载数据集
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
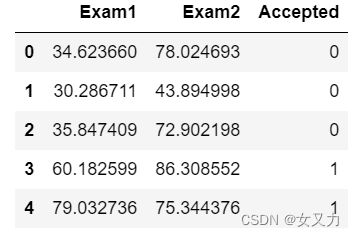
data = pd.read_csv('../data/ex2data1.txt', names=['Exam1', 'Exam2', 'Accepted'])
data.head()
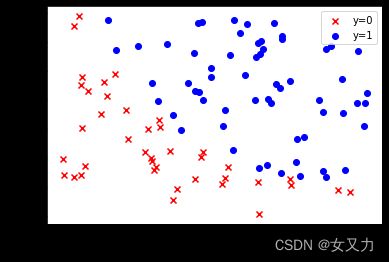
2. 数据可视化扎实
fig, ax = plt.subplots()
ax.scatter(data[data['Accepted']==0]['Exam1'], data[data['Accepted']==0]['Exam2'], c='r', marker='x', label='y=0')
ax.scatter(data[data['Accepted']==1]['Exam1'], data[data['Accepted']==1]['Exam2'], c='b', marker='o', label='y=1')
ax.legend()
ax.set(xlabel='exam1', ylabel='exam2')
plt.show()
3. 构造数据集
# 与线性回归做法一致
def get_Xy(data):
data.insert(0, 'ones', 1)
X_ = data.iloc[:, 0:-1]
X = X_.values
y_ = data.iloc[:, -1]
y = y_.values.reshape(len(y_), 1)
return X, y
X, y = get_Xy(data)
4. 定义sigmoid函数和损失函数
对于逻辑回归模型,我们构建的模型为: P ( y = 1 ∣ x ; θ ) = 1 1 + e − θ T x P(y=1|x;\theta) = \frac{1}{1 + e^{-\theta^Tx}} P(y=1∣x;θ)=1+e−θTx1
代码中( m m m表示样本维度, n n n表示样本个数): X = [ 1 x 01 x 02 ⋯ x 0 m 1 x 11 x 12 ⋯ x 1 m ⋮ ⋮ ⋮ ⋮ 1 x n 1 x n 2 ⋯ x n m ] , θ = [ θ 0 θ 1 ⋮ θ m ] X=\begin{bmatrix} 1 & x_{01} & x_{02} & \cdots & x_{0m}\\ 1 & x_{11} & x_{12} & \cdots & x_{1m} \\ \vdots & \vdots & \vdots & \vdots \\ 1 &x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix}, \theta=\begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_m \end{bmatrix} X=⎣⎢⎢⎢⎡11⋮1x01x11⋮xn1x02x12⋮xn2⋯⋯⋮⋯x0mx1mxnm⎦⎥⎥⎥⎤,θ=⎣⎢⎢⎢⎡θ0θ1⋮θm⎦⎥⎥⎥⎤
所以在实际实现中,是直接用 X X X与 θ \theta θ做内积。
在模型的数学形式确定后,剩下的就是如何去求解模型中的参数 θ \theta θ。而在已知模型和一定样本的情况下,估计模型的参数,在统计学中常用的是极大似然估计方法。即找到一组参数 θ \theta θ,使得在这组参数下,样本数据的似然度(概率)最大。
对于逻辑回归模型,假定的概率分布是伯努利分布,根据伯努利分布的定义,其概率质量函数 P M F PMF PMF为: P ( X = n ) = { 1 − p n = 0 p n = 1 P(X = n) =\left\{ \begin{array}{rcl} 1 - p & & n = 0\\ p & & n = 1 \end{array} \right. P(X=n)={1−ppn=0n=1
所以似然函数可以写成: L ( θ ) = ∏ i = 1 m P ( y = 1 ∣ x i ) y i P ( y = 0 ∣ x i ) 1 − y i L(\theta)=\prod_{i=1}^m{P(y=1|x_i)^{y_i}P(y=0|x_i)^{1-y_i}} L(θ)=i=1∏mP(y=1∣xi)yiP(y=0∣xi)1−yi
对数似然函数则为: ln L ( θ ) = ∑ i = 1 m [ y i ln P ( y = 1 ∣ x i ) + ( 1 − y i ) ln P ( y = 0 ∣ x i ) ] \ln L(\theta)=\sum_{i=1}^m[y_i\ln P(y=1|x_i) + (1 - y_i)\ln P(y=0|x_i)] lnL(θ)=i=1∑m[yilnP(y=1∣xi)+(1−yi)lnP(y=0∣xi)] ln L ( θ ) = ∑ i = 1 m [ y i ln P ( y = 1 ∣ x i ) + ( 1 − y i ) ln ( 1 − P ( y = 1 ∣ x i ) ) ] \ln L(\theta)=\sum_{i=1}^m[y_i\ln P(y=1|x_i) + (1 - y_i)\ln (1 - P(y=1|x_i))] lnL(θ)=i=1∑m[yilnP(y=1∣xi)+(1−yi)ln(1−P(y=1∣xi))]
由于在机器学习中,我们通常是对代价函数做最小化处理,所以最大化似然函数,可以在似然函数前面加个负号形成代价函数,从而转换为最小化化代价函数: c o s t ( y , p ( y ∣ x ) ) = − 1 m ∑ i = 1 m [ y i ln P ( y = 1 ∣ x i ) + ( 1 − y i ) ln ( 1 − P ( y = 1 ∣ x i ) ) ] cost(y, p(y|x))=-\frac{1}{m}\sum_{i=1}^m[y_i\ln P(y=1|x_i) + (1 - y_i)\ln (1 - P(y=1|x_i))] cost(y,p(y∣x))=−m1i=1∑m[yilnP(y=1∣xi)+(1−yi)ln(1−P(y=1∣xi))]
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def costFunction(X, y, theta):
return -np.sum(y * np.log(sigmoid(X @ theta)) + (1 - y) * np.log(1 - sigmoid(X @ theta))) / len(X)
5. 初始化参数
theta = np.zeros((3, 1))
cost_init = costFunction(X, y, theta)
cost_init
此时求得的初始化损失值为:0.6931471805599453
6. 定义梯度下降函数
损失函数关于 θ \theta θ的偏导数为: θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j := \theta_j - \alpha\frac{\partial }{\partial \theta_j}J(\theta) θj:=θj−α∂θj∂J(θ)
∂ ∂ θ j J ( θ ) = 1 m ∑ i = 1 m ( h θ ( x i ) − y i ) x i j \frac{\partial }{\partial \theta_j}J(\theta) = \frac{1}{m}\sum_{i=1}^m(h_\theta(x_i) - y_i)x_{ij} ∂θj∂J(θ)=m1i=1∑m(hθ(xi)−yi)xij
# 梯度下降函数
def gradientDescent(X, y, theta, iters, alpha):
m = len(X)
costs = []
for i in range(iters):
A = sigmoid(X @ theta)
theta = theta - alpha * X.T @ (A - y) / m
cost = costFunction(X, y, theta)
costs.append(cost)
if i % 100 == 0:
print(f'迭代次数i={i},损失函数值cost={cost}')
return costs, theta
7. 执行梯度下降函数,获取最佳参数
alpha = 0.004
iters = 200000
costs, theta_final = gradientDescent(X, y, theta, iters, alpha)
theta_final
经过计算可得最佳参数为:array([[-23.77446812], [0.20684452], [0.19996036]])
8. 预测及准确率
def predict(X, theta):
prob = sigmoid(X @ theta)
return [1 if x >= 0.5 else 0 for x in prob
y_ = np.array(predict(X, theta_final))
y_pre = y_.reshape(len(y_), 1)
acc = np.mean(y_pre == y)
acc
所得模型的准确率为:0.91
9. 可视化展示
由假设的模型可知, θ T X = 0 \theta^TX=0 θTX=0 为两类别的分界线,即 θ 0 + θ 1 x 1 + θ 2 x 2 = 0 \theta_0 + \theta_1x_1 + \theta_2x_2 = 0 θ0+θ1x1+θ2x2=0。由此,可根据 x 1 x_1 x1 计算出 x 2 x_2 x2 的值,即得到 x 2 x_2 x2 关于 x 1 x_1 x1 的函数: x 2 = − θ 0 θ 2 − θ 1 θ 2 x 1 x_2 = -\frac{\theta_0}{\theta_2} -\frac{\theta_1}{\theta_2}x_1 x2=−θ2θ0−θ2θ1x1
coef1 = -theta_final[0, 0] / theta_final[2, 0]
coef2 = -theta_final[1, 0] / theta_final[2, 0]
x1 = np.linspace(20, 100, 100)
x2 = coef1 + coef2 * x1
fig,ax = plt.subplots()
ax.scatter(data[data['Accepted']==0]['Exam1'],data[data['Accepted']==0]['Exam2'],c='r',marker='x',label='y=0')
ax.scatter(data[data['Accepted']==1]['Exam1'],data[data['Accepted']==1]['Exam2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='exam1',
ylabel='exam2')
ax.plot(x1,x2,c='g')
plt.show()
2. 线性不可分
设想你是工厂的生产主管,你要决定是否芯片要被接受或抛弃。ex2data2.txt是芯片在两次测试中的结果。
1. 读取数据并进行可视化展示
data = pd.read_csv('../data/ex2data2.txt', names=['Test1', 'Test2', 'Accepted'])
data.head()
fig, ax = plt.subplots()
ax.scatter(data[data['Accepted']==0]['Test1'],data[data['Accepted']==0]['Test2'],c='r',marker='x',label='y=0')
ax.scatter(data[data['Accepted']==1]['Test1'],data[data['Accepted']==1]['Test2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='Test1', ylabel='Test2')
plt.show()
2. 特征映射
当逻辑回归问题较复杂,原始特征不足以支持构建模型时,可以通过组合原始特征成为多项式,创建更多特征,使得决策边界呈现高阶函数的形状,从而适应复杂的分类问题。
# 特征映射:共映射到(power+1)*(power+2)/2个特征
def feature_mapping(x1, x2, power):
data = {}
for i in np.arange(power + 1):
for j in np.arange(i + 1):
data['F{}{}'.format(i-j, j)] = np.power(x1, i-j) * np.power(x2, j)
return pd.DataFrame(data)
x1 = data['Test1']
x2 = data['Test2']
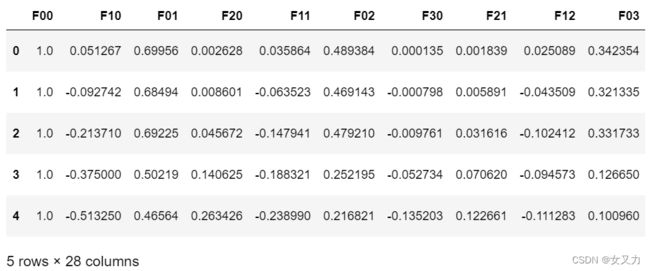
data2 = feature_mapping(x1, x2, 6)
data2.head()
3. 构造数据集
X = data2.values
y = data.iloc[:, -1].values.reshape(len(X), 1)
4. 定义sigmoid函数和损失函数
算法没有很好的拟合训练集,称为欠拟合或高偏差。算法有很强的偏见,罔顾数据的不符,先入为主地拟合一条直线,最终导致拟合训练集效果很差。
算法过度拟合数据集,称为过拟合或高方差(变量数量多,高阶项太多)。它无法泛化到新的样本中。泛化指的是模型应用到新样本的能力。
下图中依次是:低偏差低方差,低偏差高方差,高偏差低方差,高偏差高方差

解决过拟合,要么减少特征变量的数量,要么使用正则化。但是舍弃特征变量的缺点是,同时舍弃了关于问题的一些信息,我们可能不想舍弃。所以我们接下来使用正则化,保留所有的特征变量,但是减小量级或者限制 θ \theta θ 的大小。
如图所示,在原有的需要最小化的代价函数的基础上,添加了 1000 θ 3 2 + 1000 θ 4 2 1000\theta_3^2 + 1000\theta_4^2 1000θ32+1000θ42 两项,称为惩罚项。

现在我们想要 J J J 尽可能小,就是要 θ 3 \theta_3 θ3 和 θ 4 \theta_4 θ4 尽可能小,尽量接近0,就像我们去掉了 θ 3 \theta_3 θ3 和 θ 4 \theta_4 θ4,那么我们这个高阶项就近乎没有了。
正则化思想是参数值较小意味着更简单的假设模型,一般来说, θ \theta θ 的值越小,我们得到的曲线越平滑,也越简单,更不容易出现过拟合。
由于我们并不知道哪个参数该减小,所以我们选择惩罚所有参数,缩小每一个 θ j \theta_j θj 的值除了 θ 0 \theta_0 θ0 ,因为 x 0 ( i ) = 1 x_0^{(i)} = 1 x0(i)=1 ,正则化后的损失函数为:
c o s t ( y , p ( y ∣ x ) ) = − 1 m ∑ i = 1 m [ y i ln P ( y = 1 ∣ x i ) + ( 1 − y i ) ln ( 1 − P ( y = 1 ∣ x i ) ) ] + λ 2 m ∑ j = 1 m θ j 2 cost(y, p(y|x))=-\frac{1}{m}\sum_{i=1}^m[y_i\ln P(y=1|x_i) + (1 - y_i)\ln (1 - P(y=1|x_i))] + \frac{\lambda}{2m}\sum_{j=1}^m{\theta_j^2} cost(y,p(y∣x))=−m1i=1∑m[yilnP(y=1∣xi)+(1−yi)ln(1−P(y=1∣xi))]+2mλj=1∑mθj2
正则化系数 λ \lambda λ 控制两个目标之间的取舍:第一个目标是第一项,我们想更好地拟合数据,希望第一项尽可能小;第二个目标与正则化系数有关,我们要保持参数尽可能小,保持模型的相对简单,避免过拟合。 λ \lambda λ 控制这两个目标的平衡关系,过小则惩罚力度不够导致过拟合,过大则所有参数为0导致欠拟合。
梯度下降的过程为:

def sigmoid(z):
return 1 / (1 + np.exp(-z))
def costFunction(X, y, theta, lamda):
A = sigmoid(X @ theta)
m = len(X)
cost = -np.sum(y * np.log(A) + (1 - y) * np.log(1 - A)) / m
reg = np.sum(np.power(theta[1:], 2)) * lamda / (2 * m)
return cost + reg
5. 初始化参数
theta = np.zeros((28, 1))
lamda = 1
cost_init = costFunction(X, y, theta, lamda)
cost_init
得到的初始损失值为:0.6931471805599454
6. 定义梯度下降函数
def gradientDescent(X, y, theta, alpha, iters, lamda):
costs = []
m= len(X)
for i in range(iters):
reg = theta[1:] * lamda / m
reg = np.insert(reg, 0, values=0, axis=0)
theta = theta - (X.T @ (sigmoid(X @ theta) - y)) / m - reg
cost = costFunction(X, y, theta, lamda)
costs.append(cost)
if i % 1000 == 0:
print(f'迭代次数i={i},损失函数值cost={cost}')
return theta, costs
7. 寻找最佳参数
alpha = 0.001
iters = 200000
lamda = 0.1
theta_final, costs = gradientDescent(X, y, theta, alpha, iters, lamda)
8. 预测,计算准确率
def predict(X, theta):
prob = sigmoid(X @ theta)
return [1 if x >= 0.5 else 0 for x in prob]
y_ = np.array(predict(X, theta_final))
y_pre = y_.reshape(len(y_), 1)
acc = np.mean(y_pre == y)
acc
得到的准确率为:0.8389830508474576
9. 可视化展示
x = np.linspace(-1.2,1.2,200)
xx,yy = np.meshgrid(x,x)
z = feature_mapping(xx.ravel(),yy.ravel(),6).values
zz = z @ theta_final
zz = zz.reshape(xx.shape)
fig,ax = plt.subplots()
ax.scatter(data[data['Accepted']==0]['Test1'],data[data['Accepted']==0]['Test2'],c='r',marker='x',label='y=0')
ax.scatter(data[data['Accepted']==1]['Test1'],data[data['Accepted']==1]['Test2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='Test1', ylabel='Test2')
plt.contour(xx,yy,zz,0)
plt.show()