【论文笔记】Generating Radiology Reports via Memory-driven Transformer (EMNLP 2020)

论文原文：https://arxiv.org/pdf/2010.16056v2.pdf

代码链接（含数据集）：https://github.com/cuhksz-nlp/R2Gen/

 

Abstract

• generate radiology reports with memory-driven Transformer
  • a relational memory is designed to record key information of the generation process 关系存储器用于记录生成过程中的关键信息
  • a memory-driven conditional layer normalization is applied to incorporating the memory into the decoder of Transformer 应用存储器驱动的条件层规范化，将存储器纳入变压器的解码器中

 

Introduction

• memory-driven Transformer: generate radiology reports
  • relational memory 关联式存储器(RM): record the information from previous generation processes 记录来自上一代流程的信息
  • memory-driven conditional layer normalization 内存驱动的条件层规范化(MCLN): incorporate the relational memory into Transformer 将关系内存合并到Transformer中

contributions

1. propose to generate radiology reports via a novel memory-driven Transformer model 提出通过一种新的记忆驱动的Transformer模型生成放射学报告
2. propose a relational memory to record the previous generation process and the MCLN to incorporate relational memory into layers in the decoder of Transformer 提出一个关系存储器来记录以前的生成过程，并提出一个MCLN来将关系存储器合并到Transformer解码器的各个层中
3. Extensive experiments are performed and the results show that our proposed models outperform the baselines and existing models 大量的实验结果表明，我们提出的模型优于基线和现有模型
4. We conduct analyses to investigate the effect of our model with respect to different memory sizes and show that our model is able to generate long reports with necessary medical terms and meaningful image-text attention mappings 我们的模型能够生成带有必要的医学术语和有意义的图像-文本注意映射的长报告

 

The Proposed Method

treat the input from a radiology image as the source sequence $\mathbf{X}=\{{\mathbf{X}}_1,{\mathbf{X}}_2,...,{\mathbf{X}}_S\},{\mathbf{X}}_S\in {\mathbb{R}}^d$

 

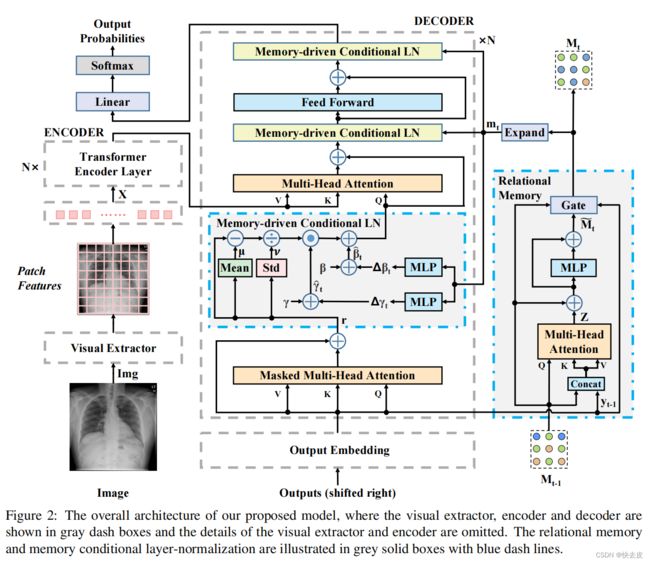
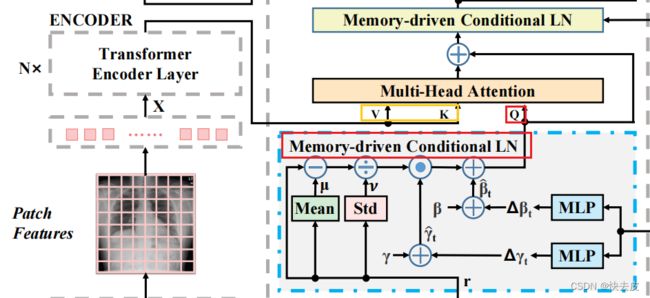
The Model Structure

Visual Extractor

视觉提取器

given a radiology image $Img$

• its $\text{X}$ are extracted by pre-trained CNN / VGG / ResNet 使用预训练的卷积神经网络
• the encoded results are used as the source sequence for all subsequent modules 编码后的结果被用作所有后续模块的源序列

process:
$$\{{\mathbf{X}}_1,{\mathbf{X}}_2,...,{\mathbf{X}}_S\}=f_v(Img)$$

• $f_v(\cdot )$: visual extractor 提取器

 

Encoder

standard encoder from Transformer 标准的编码器

process:
$$\{{\mathbf{h}}_1,{\mathbf{h}}_2,...,{\mathbf{h}}_S\}=f_e({\mathbf{X}}_1,{\mathbf{X}}_2,...,{\mathbf{X}}_S)$$

• ${\text{h}}_i$: hidden state
• $f_e(\cdot )$: encoder

 

Decoder

introduce an extra memory module to Transformer by improving the original layer normalization with MCLN for each decoding layer 通过对每个解码层用MCLN改进原始层归一化，为Transformer引入一个额外的内存模块（Relational Memory）

Transformer介绍：https://zhuanlan.zhihu.com/p/82312421

process:
$$y_t=f_d({\mathbf{h}}_1,...,{\mathbf{h}}_S,\text{MCLN}(\mathbf{R}\mathbf{M}(y_1,...,y_{t-1})))$$

• $f_d(\cdot )$: decoder

 

Objective

entire generation process can be formalized as a recursive application of the chain rule:
$$p(Y|Img)=\prod _{t=1}^T(p(y_t)|y_1,...,y_{t-1},Img)$$

• $Y=y_1,y_2,...,y_T$: target text sequence

model - maximize $p(Y|Img)$ through the negative conditional log-likelihood of $Y$ 负条件对数似然:
$${\theta }^{\ast }={\text{arg}}_{\theta }\text{max}\sum _{t=1}^T\text{log}p(y_t|y_1,...,y_{t-1},Img;\theta )$$

• $\theta$: parameters

 

Relational Memory

关联记忆网络 - 建模模式化信息

relevant $Img$ may share similar patterns in reports

• use an extra component - relational memory to enhance Transformer
  • facilitate computing the interactions among patterns and the generation process 便于计算模式之间的交互和生成过程
  • use a matrix to transfer its states over generation steps 使用矩阵在生成步骤中转移它的状态
     

matrix

• states record important pattern information with each row - represent some pattern information 状态用每一行记录重要的模式信息——表示一些模式信息
• during generation: updated step-by-step with incorporating the output from previous steps 在生成期间:通过合并前面步骤的输出逐步更新

$H$ sets of queries, keys and values via 3 linear transformations

• for each head, obtain the query 查询, key 键 and value 值 in the relational memory through:

$$\begin{gathered} \mathbf{Q}={\mathbf{M}}_{t-1}\cdot {\mathbf{W}}_{\mathbf{q}} \\ \mathbf{K}=[{\mathbf{M}}_{t-1};{\mathbf{y}}_{t-1}]\cdot {\mathbf{W}}_{\mathbf{k}} \\ \mathbf{V}=[{\mathbf{M}}_{t-1};{\mathbf{y}}_{t-1}]\cdot {\mathbf{W}}_{\mathbf{v}} \end{gathered}$$

• ${\mathbf{y}}_{t-1}$: embedding of the last output (at step $t-1$)
• $[{\mathbf{M}}_{t-1};{\mathbf{y}}_{t-1}]$: row-wise concatenation of ${\text{M}}_{t-1}$ and ${\text{y}}_{t-1}$ row-wise连接
• ${\mathbf{W}}_{\mathbf{q}},{\mathbf{W}}_{\mathbf{k}},{\mathbf{W}}_{\mathbf{v}}$: trainable weights of linear transformation of the query, key, value

 

Multi-head Module

Multi-head attention is uesd to model $Q,K,V$ so as to depict relations of different patterns 采用多头注意对Q、K、V进行建模，以刻画不同模式之间的关系

result:
$$\mathbf{Z}=\text{softmax}({\mathbf{Q}\mathbf{T}}^{\mathrm{T}}/\sqrt{d_k})\cdot \mathbf{V}$$

• $d_k$: the dimension of $\mathbf{K}$
• $\mathbf{Z}$: output of the multi-head attention module

Consider that the relational memory is performed in a recurrent manner along with the decoding process, it potentially suffers from gradient vanishing and exploding 考虑到关系存储是在解码过程中以循环的方式执行的，它可能会遭受梯度消失和爆炸

solution: introduce residual connections and a gate mechanism

• residual connections:

$$\widetilde{{\mathbf{M}}_t}=f_{mlp}(\mathbf{Z}+{\mathbf{M}}_{t-1})+\mathbf{Z}+{\mathbf{M}}_{t-1}$$

• $f_{mlp}(\cdot )$: multi-layer perceptron (MLP)

• gate mechanism:
  

• forget & input gates: balance the inputs from ${\mathbf{M}}_{t-1}$ and $y_{t-1}$

formalized as:
$$\begin{gathered} {\mathbf{G}}_t^f={\mathbf{Y}}_{t-1}{\mathbf{W}}^f+\text{tanh}({\mathbf{M}}_{t-1})\cdot {\mathbf{U}}^f \\ {\mathbf{G}}_t^i={\mathbf{Y}}_{t-1}{\mathbf{W}}^i+\text{tanh}({\mathbf{M}}_{t-1})\cdot {\mathbf{U}}^i \end{gathered}$$

• ${\mathbf{W}}^f,{\mathbf{W}}^i$: trainable weights for ${\mathbf{Y}}_{t-1}$ in each gate
• ${\mathbf{U}}^f,{\mathbf{U}}^i$: trainable weights for ${\mathbf{M}}_{t-1}$ in each gate

final output of the gate mechanism:
$${\mathbf{M}}_t=\sigma ({\mathbf{G}}_t^f)\odot {\mathbf{M}}_{t-1}+\sigma ({\mathbf{G}}_t^i)\odot \text{tanh}({\tilde{\mathbf{M}}}_t)$$

• $\odot$: Hadamard product 哈达玛积

  哈达玛积参考：https://baike.baidu.com/item/%E5%93%88%E8%BE%BE%E7%8E%9B%E7%A7%AF/18894493?fr=aladdin

• $\sigma$: sigmoid function

• ${\mathbf{M}}_t$: output of the entire relational memory module at step $t$

 

MLP

MLP: used to predict a change $\Delta {\gamma }_t$ on ${\gamma }_t$ from ${\mathbf{m}}_t$, 预测变化 update it via:
$$\begin{gathered} \Delta {\gamma }_t=f_{mlp}({\mathbf{m}}_t) \\ {\tilde{\gamma }}_t=\gamma +\Delta {\gamma }_t \end{gathered}$$
$\Delta {\beta }_t$ and ${\tilde{\beta }}_t$ are performed by:
$$\begin{gathered} \Delta {\beta }_t=f_{mlp}({\mathbf{m}}_t) \\ {\tilde{\beta }}_t=\beta +\Delta {\beta }_t \end{gathered}$$
then the predicted ${\tilde{\beta }}_t$ and ${\tilde{\gamma }}_t$ are applied to the mean and variance results of the multi-head self-attention from the previous generated outputs: 应用于先前生成的输出的多头自我注意的均值和方差结果
$$f_{mcln}(\mathbf{r})={\hat{\gamma }}_t\odot \frac{\mathbf{r}-\mu }{v}+{\hat{\beta }}_t$$

• $\mathbf{r}$: output from the previous module
• $\mu ,v$: mean and standard deviation 平均值和标准差 of $\mathbf{r}$
• $f_{mcln}(\mathbf{r})$: result for MCLN
  • then fed to the next module (1st & 2nd MCLN)
  • or used as the final output for generation (3rd MCLN)

 

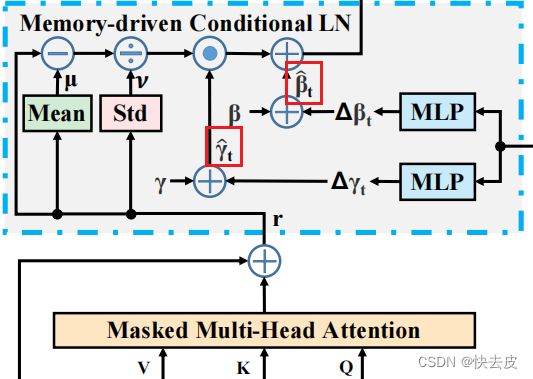
Memory-driven Conditional Layer Normalization (MCLN)

基于记忆的层归一化

• incorporate the relational memory 合并关系存储器 to enhance the decoding of Transformer
  • by feeding its output ${\mathbf{M}}_t$ to $\gamma$ and $\beta$

3 MCLNs in each Transformer decoding layer

• first MCLN: output is functionalized as the query to be fed into the following multi-head attention module together with the hidden states from the encoder as key and value

• the output of the relational memory ${\mathbf{M}}_t$ is expended into a vector ${\mathbf{m}}_t$ by simply concatenating all rows from ${\mathbf{M}}_t$

 

Experiment Settings

• datasets: IU X-RAY & MIMIC-CXR

• baselines:

  • BASE: vanilla Transformer

    • 3 layers, 8 heads, 512 hidden units without other extensions and modifications

  • BASE+RM: the relational memory is directly concatenated to the output of the Transformer ahead of the softmax at each time step 关系内存直接连接到Transformer的输出，位于softmax之前

    • to demonstrate the effect of using memory as an extra component instead of integration within the Transformer 演示将内存作为额外组件而不是集成到Transformer中的效果

• learning rate: 5e-5 and 1e-4 for the visual extractor and other parameters

• for MCLN: use two MLPs to obtain $\Delta {\gamma }_t$ and $\Delta \beta$ where they do not share parameters

 

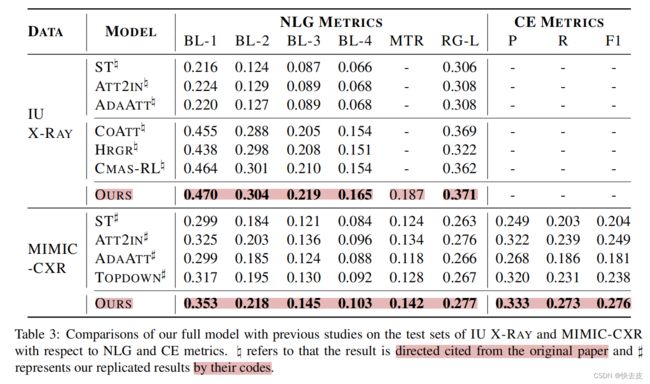
Results and Analyses

hyper-parameters & generation results

 

Memory Size

$|S|\in \{1,2,3,4\}$: numbers of memory slots

• too large memory may introduce redundant and invalid information 冗余无效信息

 

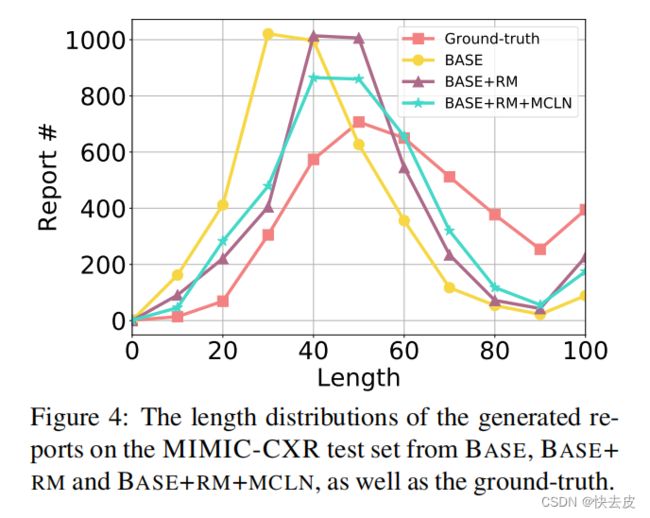
Report Length

• memory provides more detailed information for the generation process

  • decoder tends to produce more diversified 多样化 outputs than the original Transformer

• 2 important factors to enhance radiology report generation:

  • memory
  • the way of using memory

 

Case Study

1. start from reporting abnormal findings
2. conclude with potential deseases

BASE+RM+MCLN: almost cover all of the necessary medical terms in the ground-truth reports

the intermediate imgae-text correspondences for several words from the multi-head attentions in the first layer of the decoders:

• BASE+RM+MCLN is better at aligning the locations with the indicated disease or parts 好地将位置与疾病或部位对齐

our model: improves the interaction between the images and the generated texts

 

Error Analysis

• class imbalance is severe on the datasets and affects the model training and inference 类的不平衡严重影响了模型的训练和推理
  • majority voting is observed in the generation process 在生成过程中遵守多数表决

 

Conclusion

• memory-driven Transformer
  • relational memory: used to record the information from previous generation processes 关系存储器:用于记录来自上一代进程的信息
  • layer normalization mechanism: to incorporate the memory into Transformer 层归一化机制:将内存合并到Transformer

our model is able to generate long reports with necessary medical terms and meaningful image-text attention mappings 我们的模型能够生成带有必要的医学术语和有意义的图像-文本注意力映射的长报告。

 
 
借鉴：https://blog.csdn.net/c9Yv2cf9I06K2A9E/article/details/114695686