LATEX数学公式教程

一、命令与环境

1.1 命令的定义与使用方式

不同于其他编程语言(C/C++, Python等)会使用关键词,函数和类来实现程序，Latex语法中大多以命令的形式存在。其中，每一个命令都会有具体的功能,如标题制作,目录制作,或者是设置文档的编码格式等等

LATEX命令（宏）的格式为：

1. 无参数

   \commad
   

2. 有n个参数

   \command{arg1}{arg2}...{argn}
   

3. 有可选参数

   \command[arg1]...[argn]
   

其中，命令都以反斜线\开头，后接命令名，命令名或者是一串字母，或是单个符号。命令可以带一些参数，如果命令的参数不止一个字符（不包括空格)，就必须用花括号括起来。可选参数如果出现，则用方括号括起来。

1.2 环境的定义与使用方式

我们编写的文档内容为了避免代码和我们书写的正文内容混杂,我们从夹杂代码和正文内容的纯文本的连续上下文中划分出部分空间,这部分空间将作为独立的整体,我们可以将正文内容写在这些空出来的部分中。对于这些空间,我们可以提前使用一些命令,设定好这些空间的环境,即设定好这些空间的环境,即编译好之后最终的展示格式,因此环境其实就是我们为特定部分的正文设定的格式,这个特定部分可以是后面的全文,也可以是正文的部分,例如一段话,一张图片等等

LATEX环境的一般格式为：

1. 不带参数

   \begin{环境名}
   环境内容
   \end{环境名}
   

2. 带参数或可选参数

\begin{环境名}[可选参数]{其他参数}
环境内容
\end{环境名}

二、数学模式

2.1 工作模式

TEX有多种工作模式:

• 水平模式：输人一行文字时我们在水平模式，在水平模式下，文字、符号等各种排版元素，也就是各种盒子，都要从左到右依次水平排列;
• 垂直模式：当折行分段的时候又自动进入了垂直模式，在垂直模式下，各种盒子都从上到下依次垂直排列;
• 数学模式：数学模式是其中最吸引人的模式。在数学模式中，输入的字符都有专门的意义，盒子的排列也遵循单独的一套特殊规则，以适应结构复杂的各种数学公式。

在数学模式下，符号会使用单独的字体，字母通常是倾斜的意大利体，数字和符号则是直立体。另外，数学符号之间的距离也与一般的水平模式不同。

举个例子：

数学模式：$a+b=b+a$，$1+2=2+1$

普通模式：a+b=b+a，1+2=2+1

因此，在排版数学公式时，即使是没有任何特殊符号的算式1＋1，或者简单地一个字母变量x，也要必须进入数学模式，使用$1+1$、$x$，而不应该用排版普通文字的方式搞成1+1、x。

值得注意的是，显示公式后面如果有标点符号，应该放在数学环境内部，紧接着公式。而且因为数学模式下不能使用汉字，所以一般就使用西文的半角标点。

2.2 数学公式

TEX有两种数学公式：

• 行内（inline）数学公式 或正文（in-text）数学公式：一种夹杂在行文段落中的公式
• 显示（displayed）数学公式（或行间公式、列表公式）：单独占据整行居中展示出来，显示数学环境更适合表现更复杂的数学内容

行内公式输入方式：

1. 单个美元符号(推荐)：$数学公式$

2. 命令格式：\(和\)

   \(a+b\)
   

3. 环境格式：math

   \begin{math}a+b\end{math}
   

4. 自定义命令，主要使用\ensuremath

显示公式输入方式：

1. 连续两个美元符号：$$数学公式$$

2. 命令格式：\[ 和\]

   \[a+b\]
   

3. 环境格式：displaymath

   \begin{displaymath}a+b\end{displaymath}
   

2.3 amsmath宏包

\text命令

数学模式和普通文本模式不同,在数学模式中不仅字符的字体、间距不同，而且空格也会被忽略，汉字也不能直接用在数学模式中，就是西文文本也不能直接输入。amsmath提供的\text命令就可以用来在数学公式中插入文字。

三、数学结构

数学公式不是简单的符号连接堆砌，而是特定数学结构的组合。数学j结构就相当于数学公式的骨架。

3.1 上标与下标

上标用特殊字符^表示，下标用特殊字符_表示。如果上下标的内容多于一个字符，需要用 {}将这些内容括成一个整体。上下标可以嵌套，也可以同时使用。

举个例子，a_3=2^{i+j} $a_3=2^{i+j}$

特殊上下标：

撇号’ ：可以用符号\prime 或者 ‘。 例如，b'_0 = b''_0 , $b_0^{\prime }=b_0^{\prime \prime }$

角度符号： 利用\circ表示 。例如 ， A=90^\circ, $A=90^{\circ }$

张量：利用 \tensor命令 。例如，\tensor[^a_b^c_d]{M}{^a_b^c_d} ,

amsmath宏包选项

amsmath宏包的几个选项可以控制显示公式中一般巨算符和积分号的上下标位置，除此之外，也可以手工改变上下标的位置。

在上下标前面用\limits命令会使上下标在正上正下方，这正是通常上下限( limits)的排版方式。而使用\nolimits则使上下标在角上，例如:

\iiint\limits_D \mathrm{d}f = \max\nolimits_D g
$$\underset{D}{\iiint }\mathrm{d}f={\max }_{D}g$$

3.2 上下画线与花括号

(1)\overline和\underline命令可用来在公式的上方和下方划横线，而且这种结构可以任意嵌套或与其他数学结构组合。例如：

\overline{a+b} = \overline a + \overline b , $\overline{a+b}=\overline{a}+\overline{b}$

\overline{\underline{\underline a} + \overline{b}^2 }, $\overline{\underline{\underline{a}}+{\overline{b}}^2}$

(2)amsmath 提供了在公式上下加箭头的命令，使用方法与\overline和 \underline类似:

(3)除了横线和箭头，数学公式上下还可以使用\overbrace和 \underbrace带上花括号，并且可以在花括号上做批注，如:

\overbrace{a+b+c} = \underbrace{1+2+3}, $a+b+c=1+2+3$

\overbrace{a+b+c} ， $\stackrel{\text{共60项相加}}{a+b+\cdots +c}$

(4) 类似地，mathtools宏包还提供了在数学公式上下加方括号的命令:

\underbracket[(线宽)][(伸出高度)]{(内容)}
loverbracket[(线宽)][(伸出高度)]{(内容)}

例如， \underbracket{\overbracket{1+2}+3}

3.3 分式

分式( fraction )也是数学公式中极为常见的结构。在BTgX中,分式用\frac<分子><分母>得到。在行内公式和显示公式中，分式的大小是不同的。行内公式中分子分母都用较小的字号排版，以免超出文本行高度。如:

\frac 12 + \frac 2b = \frac {4+x}{x}， $\frac{1}{2}+\frac{2}{b}=\frac{4+x}{x}$

有时需要指定较大或较小的分式，则可以使用amsmath提供的 \dfrac和 \tfrac分别指定显示格式( display style）和正文格式( text style)的分式。

3.4 根式

根式是又一种常见的数学结构，在LATEX中用单参数的命令\sqrt得到，同时可以带一个可选参数，表示开方的次数，如:

\sqrt[3]{8}=2， $\sqrt[3]{8}=2$

3.5 矩阵

最后一类数学结构是矩阵( matrix )。在基本TEX中，矩阵是用与Plain TEX一样的命令\matrix和\pmatrix排版的。矩阵使用amsmath提供的一系列矩阵环境排版，各种矩阵环境的区别在于外面的括号不同:

在矩阵环境中，不同的列用符号&分隔，行用\\分隔，矩阵每列中元素居中对齐，例如:

\begin{pmatrix} 
   a_{11}& a_{12} & a_{13} \\
   0    &  a_{22} &  1        \\
    0    &  a_{32} &  1        
 \end{pmatrix}

$$\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ 0& a_{22}& 1\\ 0& a_{32}& 1\end{array}\right)$$

在矩阵中经常使用各种省略号，即 \dots, \vdots,\ddots。(amsmath 还提供了可以跨多列的省略号\hdotsfor{<列数>})

\begin{bmatrix} 
   a_{11} & \dots    & a_{1n} \\
          &  \ddots  & \vdots        \\
    0     &          &  a{nn}
 \end{bmatrix}_{n \times n}

$${\left[\begin{array}{ccc}{a}_{11}& \dots & a_{1n}\\ & \ddots & ⋮\\ 0& & ann\end{array}\right]}_{n\times n}$$

四、符号与类型

如果说有限的几种数学结构确定了数学公式的骨架，那么无比丰富的数学符号才真正构成数学公式的血肉。"符号大全”Pakin [192]所收录的近6000个符号，半数都是数学符号。有条理地归纳这些数学符号，熟记常用符号的命令，了解符号的分类和使用规律，才可能真正熟练地使用LATEX的数学功能。
LATEX中的数学符号是由专门的数学字体提供的。有的符号可以直接从键盘上输入，如字母a,b,x或符号+,=,0，但大部分的符号需要使用LATEX命令输入。按照符号的意义和排版方式的不同，数学符号可以分成8个类别: 普通符号、巨算符、二元运算符、关系符、开符号、闭符号、标点和变量族。变量族（一般就是字母）和普通符号性质类似，二元运算符与关系符性质类似，开符号和闭符号合起来就是完整的括号，因此下面把它们归并为同类，分类说明每类数学符号。

4.1 字母表与普通符号

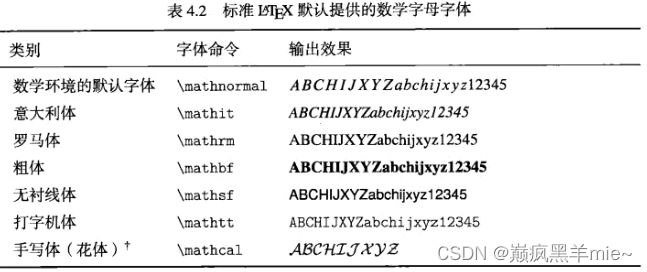
字母表是数学符号最基本的内容。拉丁字母$A,B,C,x,y,z$等都可以直接从键盘输入，默认使用意大利形状。
数学字母可以使用多种字体，数字字体命令与正文字体命令语法类似，如$\mathbf{X}$得到直立粗体的$\mathbf{X}$。

数学公式中还经常使用希腊字母和少量其他类型的字母。

此外，还有一些符号可同时用在文本模式和数学模式中(大多用在文本模式中),

4.2 数学算子

数学算子通常会与前后的符号都有一小段间距。
数学算子分为两种，第一类是类似求和号$\sum$、积分号$\int$的算子，它们的大小是随显示公式和行内公式变化的，而且通常比一般的数学符号大一些，因而又被称为巨算符( large operator )。

当然，也可以用\limits 和 \nolimits手工控制巨算子的位置为上下限位置还是角标位置。

第二类数学算子是文字名称的算子,它们用直立的罗马体排印。

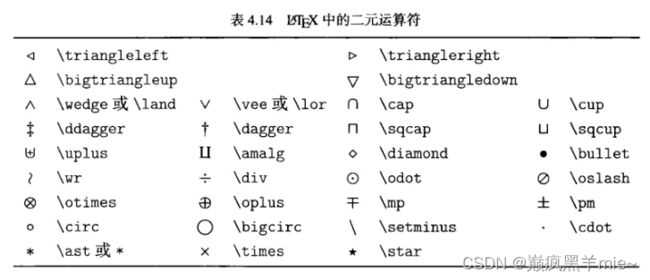
4.3 二元运算符与关系符

二元运算符与关系符都是用在公式中间，在符号的两边留有一定间距。运算符的间距小一些，关系符的间距略大一些。尽管二者的差别非常小，肉眼基本不能区分，不过，类型的差别可以帮助TEX区分公式的不同情况，好像TEX理解公式一样。

4.4 括号与界定符

4.5 标点

五、多行公式

5.1 罗列多个公式

如果问什么是显示方程的基本输入方法，那么回答便是使用编号的equation环境和不编号的equation*环境，但是里面的换行命令\\是无效的。输人多行数学公式最基本的方法与它如出一辙，就是使用gather和gather(不编号）环境，不同的仅仅是可以使用\\进行换行。
$$\begin{array}{c}2+1=1+2=3\\ 3+5=8\end{array}$$

$$\begin{array}{c}2+1=1+2=3\\ 3+5=8\end{array}$$

gather环境得到的公式是每行居中的，align环境则允许公式按等号或其他关系符对齐，在关系符前加&表示对齐。align功能相同，但不编号。align和 align环境还允许排列多列对齐的公式，列与列之间仍使用&分隔:

5.2 拆分单个公式

除了multline环境，更常用的可能就是split环境了。split环境并不开始一个数学公式，它用在equation、gather等数学环境里面，可以把单个公式拆分成多行;同时支持类似align环境那样的对齐方式(但不能对齐多列公式)，例如:

split环境与align的最大区别就是split环境不产生编号，编号仍然由外面的数学环境产生，因此两行的公式产生的编号仍在两行中间;而align环境本身就是数学环境，它会给每一行公式产生一个编号。

5.3 将公式组合成块

最为常见的是cases环境，它在几行公式前面用花括号括起来，用来表示几种不同的情况。每行公式中使用&分隔为两部分，通常表示值和后面的条件，例如:

D(x)=
\begin{cases}
1, & \text{if } x=2    \\
2, & \text{if } x=6
\end{cases}

$$D(x)=\{\begin{array}{ll}1,& \text{if }x=2\\ 2,& \text{if }x=6\end{array}$$

参考资料

刘海洋的书籍《LATEX入门》