【图表示学习】图注意力网络GAT
一、简介
CNN只能用来解决grid-like结构的数据。有很多任务的数据无法表示成grid-like结构,但可以表示成为图结构。GAT(Graph Attention Networks)就是一种处理图结构数据的神经网络。该网络是基于注意力机制实现的。
二、GAT结构
1.图注意力层的输入与输出
图注意力层(Graph Attentional Layer)是构成整个GAT的唯一种类的层。
该层的输入是多个节点的特征, h = { h 1 ⃗ , h 2 ⃗ , … , h N ⃗ } , h i ⃗ ∈ R F \textbf{h}=\{\vec{h_1},\vec{h_2},\dots,\vec{h_N}\},\vec{h_i}\in\mathbb{R}^F h={h1,h2,…,hN},hi∈RF,其中 N N N是节点数量, F F F是每个节点的特征数量。
该层的输出是这些节点的新特征, h ′ = { h 1 ′ ⃗ , h 2 ′ ⃗ , … , h N ′ ⃗ } , h i ′ ⃗ ∈ R F ′ \textbf{h}'=\{\vec{h_1'},\vec{h_2'},\dots,\vec{h_N'}\},\vec{h_i'}\in\mathbb{R}^{F'} h′={h1′,h2′,…,hN′},hi′∈RF′,其中 F ′ F' F′是新特征的维度。
2.注意力系数的计算
注意力机制的核心是计算各个部分对最终目标的贡献程度,这个贡献程度就是注意力系数。在图结构中,注意力系数是指某个节点对当前节点的贡献程度。具体来说,在GAT中节点 j j j的特征对节点 i i i特征的贡献程度表示为 e i j e_{ij} eij,其计算公式为
e i j = a ( W h i ⃗ , W h j ⃗ ) e_{ij}=a(\textbf{W}\vec{h_i},\textbf{W}\vec{h_j}) eij=a(Whi,Whj)
其中 W ∈ R F ′ × F \textbf{W}\in\mathbb{R}^{F'\times F} W∈RF′×F, a a a是计算两个向量相似度的函数。在论文的实验中函数 a a a使用单层前馈网络,即
a ( x , y ) = L e a k y R e L U ( a ⃗ T [ x ∣ ∣ y ] ) a(x,y)=LeakyReLU(\vec{\textbf{a}}^T[x||y]) a(x,y)=LeakyReLU(aT[x∣∣y])
其中, L e a k y R e L U LeakyReLU LeakyReLU是激活函数, a ⃗ ∈ R 2 F ′ \vec{\textbf{a}}\in\mathbb{R}^{2F'} a∈R2F′, ∥ \Vert ∥表示向量拼接。
3.Masked Attention机制
在GAT中,注意力机制只作用在一阶相邻节点(当然,也可以作用在更高阶),为了统一量纲这里使用 s o f t m a x softmax softmax函数对注意力系数进行标准化
α i j = s o f t m a x j ( e i j ) = e x p ( e i j ) ∑ k ∈ N i e x p ( e i k ) \alpha_{ij}=softmax_j(e_{ij})=\frac{exp(e_{ij})}{\sum_{k\in\mathcal{N}_i}exp(e_{ik})} αij=softmaxj(eij)=∑k∈Niexp(eik)exp(eij)
其中, j ∈ N i j\in\mathcal{N}_i j∈Ni, N i \mathcal{N}_i Ni表示节点 i i i的邻居节点。
这里将计算 α i j \alpha_{ij} αij的所有部分展开,
α i j = e x p ( L e a k y R e L U ( a ⃗ T [ W h ⃗ i ∣ ∣ W h ⃗ j ] ) ) ∑ k ∈ N i e x p ( L e a k y R e L U ( a ⃗ T [ W h ⃗ i ∣ ∣ W h ⃗ k ] ) ) \alpha_{ij}=\frac{exp(LeakyReLU(\vec{\textbf{a}}^T[\textbf{W}\vec{h}_i||\textbf{W}\vec{h}_j]))}{\sum_{k\in\mathcal{N}_i}exp(LeakyReLU(\vec{\textbf{a}}^T[\textbf{W}\vec{h}_i||\textbf{W}\vec{h}_k]))} αij=∑k∈Niexp(LeakyReLU(aT[Whi∣∣Whk]))exp(LeakyReLU(aT[Whi∣∣Whj]))
得到标准化的注意力系统 α i j \alpha_{ij} αij后,使用这些系数进行线性合并,得到节点 i i i的新特征,即
h i ′ ⃗ = σ ( ∑ j ∈ N i α i j W h j ⃗ ) \vec{h_i'}=\sigma\Big(\sum_{j\in\mathcal{N}_i}\alpha_{ij}\textbf{W}\vec{h_j}\Big) hi′=σ(j∈Ni∑αijWhj)

4. 多头机制与输出层
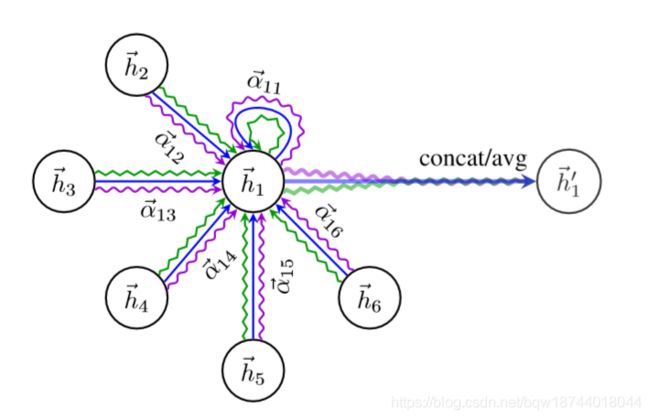
为了能够更稳定的学习新特征,引入了多头机制。这里假设有 K K K个独立的注意力机制,那么多头注意力机制就是将各个注意力特征进行合并
h i ′ ⃗ = ∥ k = 1 K σ ( ∑ j ∈ N i α i j k W k h j ⃗ ) \vec{h_i'}=\Vert_{k=1}^K\sigma\Big(\sum_{j\in\mathcal{N}_i}\alpha_{ij}^k\textbf{W}^k\vec{h_j}\Big) hi′=∥k=1Kσ(j∈Ni∑αijkWkhj)
在网络的最终层执行多头注意力机制,不再使用拼接,而使用平均,并且延期使用激活函数(softmax、sigmoid等)
h i ′ ⃗ = σ ( 1 K ∑ k = 1 K ∑ j ∈ N i α i j k W k h j ⃗ ) \vec{h_i'}=\sigma\Big(\frac{1}{K}\sum_{k=1}^K\sum_{j\in\mathcal{N}_i}\alpha_{ij}^k\textbf{W}^k\vec{h_j}\Big) hi′=σ(K1k=1∑Kj∈Ni∑αijkWkhj)
三、GAT的优势
- 计算高效。自注意力层可以并行化,计算输出特征也可以并行化。
- 为不同的节点分配不同的重要度。
- 图不必是无向的。
- 直接适用于归纳学习(inductive learning)。
- 直接作用于领域,且不做任何顺序假设。