机器学习(一)基于逻辑回归的分类预测(入门篇)
机器学习(一)基于逻辑回归的分类预测(入门篇)
- 1 线性回归基本概念
-
- 1.1 什么是回归
- 1.2 线性回归
- 1.3 损失函数
- 1.4 最小二乘估计
- 1.5.线性回归小结
- 2 多元线性回归
-
- 2.1 多元线性回归算式
- 2.2 多元线性回归损失函数
- 2.3 对线性回归模型
- 2.4 广义线性模型
- 3 逻辑回归(LR)
-
- 3.1 什么是逻辑回归?
- 3.2 什么是Sigmoid函数?
- 3.3 逻辑回归的损失函数
- 3.4 使用逻辑回归进行分类预测(demo)
·本人是机器学习小白一枚,今天算是我的第一门入门课程,说实话,拿到学习资料,我无从下手,虽然我心里大概晓得这是要干啥,但是我并不知道好多名词到底是该怎么解释,故,留下本笔记,本笔记适合于从零开始第一次学习机器学习的小白看看,算是入个门吧。
1 线性回归基本概念
学习逻辑回归之前,先了解线性回归的一些基本概念。为什么要理解线性回归呢?线性回归和逻辑回归很有关联(简单理解成先有前者,后者是在前者基础上发展起来的)。此刻姑且认为:要想理解逻辑回归,就从线性回归来开始理解。线性回归简单啊,离我们所学过的知识最接近,最能接受和理解。
- 本基础参考知乎一篇文章《用人话讲明白线性回归LinearRegression》
1.1 什么是回归
回归就是预测一系列连续的值,分类就是预测一系列离散的值
- 线性“回归”,这个回归(regression)和我们平时说的“回归祖国”的回归(return)是两个含义完全不同的词,模型的目的是预测,方式是“回归”,有“倒推”之意在里面。(倒推就是先建立线性模型(包含系数)然后用训练数据来倒推出误差最小的参数。现在不理解“倒推”没关系,学到后面再回来理解就能接受啦)
- 那么,这个回归究竟是什么意思呢?其实回归算法是相对分类算法而言的,对比举例如下:
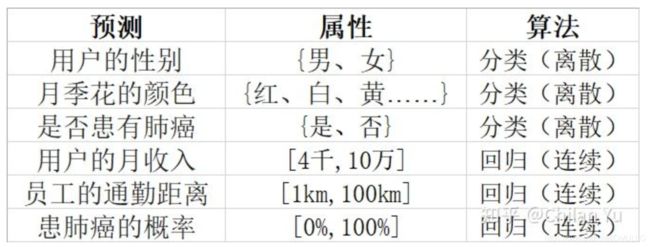
- 你一定会发现,有时分类问题也可以转化为回归问题,例如刚刚举例的肺癌预测,我们可以用回归模型先预测出患肺癌的概率,然后再给定一个阈值,例如50%,概率值在50%以下的人划为没有肺癌,50%以上则认为患有肺癌。- 这种分类问题的用连续的回归算法来预测,最常用的就是逻辑回归,后面我们会讲到。
1.2 线性回归
线性回归可以说是用法非常简单、用处非常广泛、含义也非常容易理解的一类算法,作为机器学习的入门算法非常合适。我们上中学的时候,都学过二元一次方程,我们将y作为因变量,x作为自变量,得到方程:
y = β 0 + β 1 x y=\beta_0+\beta_1x y=β0+β1x
当给定参数 β 0 \beta_0 β0和 β 1 \beta_1 β1的时候,画在坐标图内是一条直线(这就是“线性”的含义)。当我们只用一个x来预测y,就是一元线性回归,也就是在找一个直线来拟合数据。比如,我有一组数据画出来的散点图,横坐标代表广告投入金额,纵坐标代表销售量,线性回归就是要找一条直线,并且让这条直线尽可能地拟合图中的数据点。

这里我们得到的拟合方程是 y = 0.0512 x + 7.1884 y = 0.0512x + 7.1884 y=0.0512x+7.1884 ,此时当我们获得一个新的广告投入金额后,我们就可以用这个方程预测出大概的销售量。
数学理论的世界是精确的,譬如你代入 x = 0 x=0 x=0 就能得到唯一的 y ^ \hat{y} y^ , y ^ \hat{y} y^ =7.1884(y上面加一个小帽子hat,表示这个 y ^ \hat{y} y^ 不是我们真实观测到的,而是估计值)。但现实世界中的数据就像这个散点图,我们只能尽可能地在杂乱中寻找规律。用数学的模型去拟合现实的数据,这就是统计。统计不像数学那么精确,统计的世界不是非黑即白的,它有“灰色地带”,但是统计会将理论与实际间的差别表示出来,也就是“误差”。
因此,统计世界中的公式会有一个小尾巴 μ \mu μ,用来代表误差,即:
y = β 0 + β 1 x + μ y=\beta_0+\beta_1x+\mu y=β0+β1x+μ
1.3 损失函数
那既然是用直线拟合散点,为什么最终得到的直线是y = 0.0512x + 7.1884,而不是下图中的y = 0.0624x + 5呢?这两条线看起来都可以拟合这些数据啊?毕竟数据不是真的落在一条直线上,而是分布在直线周围,所以我们要找到一个评判标准,用于评价哪条直线才是最“合适”的。
我们先从残差说起。残差说白了就是真实值和预测值间的差值(也可以理解为差距、距离),用公式表示是( y ^ = f ( x ) \hat{y}=f(x) y^=f(x)就是预测值):
y = y − y ^ y=y-\hat{y} y=y−y^

对于某个广告投入 x i x_i xi ,我们有对应的实际销售量 y i y_i yi,和预测出来的销售量 y i ^ \hat{y_i} yi^(通过将 i _i i 代入公式 y = β 0 + β 1 x y=\beta_0+\beta_1x y=β0+β1x计算得到),计算 e i = y i − y i ^ e_i=y_i-\hat{y_i} ei=yi−yi^ 的值,再将其平方(为了消除负号),对于我们数据中的每个点如此计算一遍,再将所有的 e i 2 e_i^2 ei2 相加,就能量化出拟合的直线和实际之间的误差。
用公式表示就是:
Q = ∑ 1 n ( y i − y i ^ ) 2 = ∑ 1 n ( y i − ( β 0 ^ + β 1 ^ x ) ) 2 Q=\sum\limits_1^n(y_i-\hat{y_i})^2=\sum\limits_1^n(y_i-(\hat{\beta_0}+\hat{\beta_1}x))^2 Q=1∑n(yi−yi^)2=1∑n(yi−(β0^+β1^x))2
这个公式是残差平方和,即SSE(Sum of Squares for Error),在机器学习中它是回归问题中最常用的损失函数。
现在我们知道了损失函数是衡量回归模型误差的函数,也就是我们要的“直线”的评价标准。这个函数的值越小,说明直线越能拟合我们的数据。
既然我们知道,当损失函数的结果值越小,表示预测结果跟真实结果越接近,表明我们的模型越准确。所以呢?当损失函数取最小值当时候,是不是能确定我们模型中定义的参数 β 0 \beta_0 β0和 β 1 \beta_1 β1呢?
1.4 最小二乘估计
我们不禁会问,这个 β 0 \beta_0 β0和 β 1 \beta_1 β1的具体值究竟是怎么算出来的呢?
我们知道,两点确定一线,有两组x,y的值,就能算出来 β 0 \beta_0 β0和 β 1 \beta_1 β1。但是现在我们有很多点,且并不正好落在一条直线上,这么多点每两点都能确定一条直线,这到底要怎么确定选哪条直线呢?
当给出两条确定的线,如y = 0.0512x + 7.1884,y = 0.0624x + 5时,我们知道怎么评价这两个中哪一个更好,即用损失函数评价。那么我们试试倒推一下?
以下是我们最头疼的数据公式推导,我尽量对每个公式作解释说明。
给定一组样本观测值 x i x_i xi, y i y_i yi(i=1,2,…n),要求回归函数尽可能拟合(就是去预测)这组值。普通最小二乘法给出的判断标准是:残差平方和的值达到最小。
我们再来看一下残差平方和的公式:
Q = ∑ 1 n ( y i − y i ^ ) 2 = ∑ 1 n ( y i − ( β 0 ^ + β 1 ^ x ) ) 2 Q=\sum\limits_1^n(y_i-\hat{y_i})^2=\sum\limits_1^n(y_i-(\hat{\beta_0}+\hat{\beta_1}x))^2 Q=1∑n(yi−yi^)2=1∑n(yi−(β0^+β1^x))2
这个公式是一个二次方程,我们知道一元二次方程差不多长下图这样:
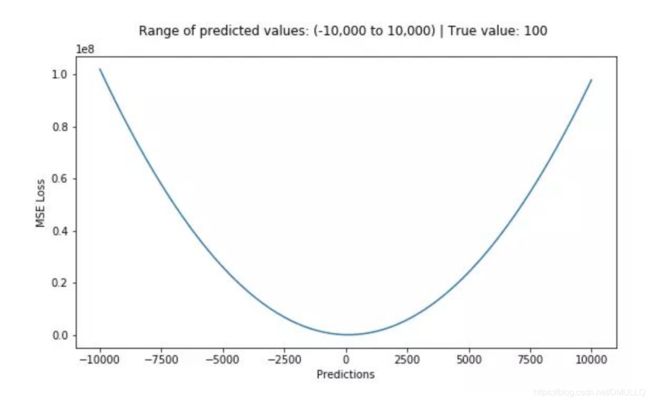
上面公式中的 β 0 \beta_0 β0 和 β 1 \beta_1 β1 未知,有两个未知参数的二次方程,画出来是一个三维空间中的图像,类似下面:
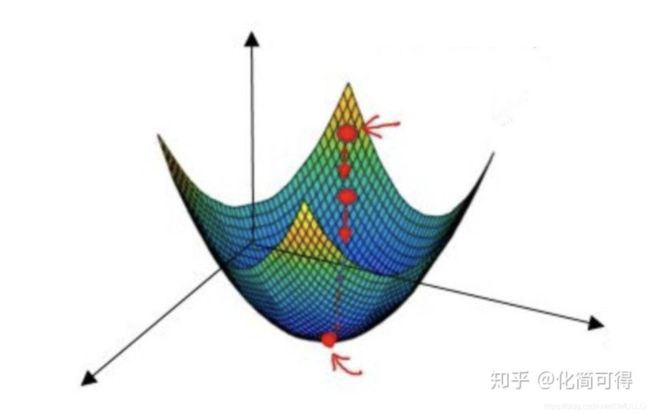
这类函数在数学中叫做凸函数,还记得微积分知识的话,就知道导数为0时,Q取最小值,因此我们分别对 β 0 \beta_0 β0 和 β 1 \beta_1 β1求偏导并令其为0:
∂ Q ∂ β 0 = 2 ∑ 1 n ( y i − β o ^ − β 1 ^ x i ) = 0 \frac{\partial{Q}}{\partial{\beta_0}}=2\sum\limits_1^n(y_i-\hat{\beta_o}-\hat{\beta_1}x_i)=0 ∂β0∂Q=21∑n(yi−βo^−β1^xi)=0
∂ Q ∂ β 1 = 2 ∑ 1 n ( y i − β o ^ − β 1 ^ x i ) x i = 0 \frac{\partial{Q}}{\partial{\beta_1}}=2\sum\limits_1^n(y_i-\hat{\beta_o}-\hat{\beta_1}x_i)x_i=0 ∂β1∂Q=21∑n(yi−βo^−β1^xi)xi=0
x i x_i xi, y i y_i yi(i=1,2,…n)都是已知的,全部代入上面两个式子,就可求得 β 0 \beta_0 β0 和 β 1 \beta_1 β1 的值啦。这就是最小二乘法,“二乘”是平方的意思。
1.5.线性回归小结
线性回归的定义,是利用最小二乘函数对一个或多个自变量之间关系进行建模的方法。现在我们看这个定义,是不是觉得不难理解了呢?
2 多元线性回归
2.1 多元线性回归算式
以上举的例子是一维的例子(x只有一个),如果有两个特征,就是二元线性回归,要拟合的就是二维空间中的一个平面。如果有多个特征,那就是多元线性回归,
最后再提醒一点,做线性回归,不要忘了前提假设是y和x呈线性关系,如果两者不是线性关系,就要选用其他的模型啦。
f ( x i ) = β 0 + β 1 x i 1 + β 2 x i 2 + ⋯ + β p x i p f(x_i)=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+\dots+\beta_px_{ip} f(xi)=β0+β1xi1+β2xi2+⋯+βpxip
其中, β 0 … β p \beta_0\dots\beta_p β0…βp 表示p个属性每个的参数(权重); x i 0 … x i p x_{i0}\dots x_{ip} xi0…xip 表示第 i 组样本(每组样本都有p个属性)。
把上面式子写成向量形式:
f ( x i ) = β T x i + β 0 = B X f(x_i)=\beta^Tx_i+\beta_0=BX f(xi)=βTxi+β0=BX
其中, β = [ β 1 β 2 ⋮ β p ] \beta= \begin{bmatrix} \beta_1 \\ \beta_2 \\ \vdots\\ \beta_p \\ \end{bmatrix} β=⎣⎢⎢⎢⎡β1β2⋮βp⎦⎥⎥⎥⎤则, β T = [ β 1 β 2 ⋯ β p ] \beta^T= \begin{bmatrix} \beta_1 & \beta_2& \cdots& \beta_p \end{bmatrix} βT=[β1β2⋯βp], x i = [ x 11 x 21 ⋯ x i 1 x 12 x 22 ⋯ x i 2 ⋮ ⋮ ⋱ ⋮ x 1 p x 2 p ⋯ x i p ] x_i=\begin{bmatrix} x_{11} &x_{21}&\cdots&x_{i1} \\ x_{12} &x_{22}&\cdots&x_{i2} \\ \vdots&\vdots&\ddots&\vdots&\\ x_{1p} &x_{2p}&\cdots&x_{ip} \\ \end{bmatrix} xi=⎣⎢⎢⎢⎡x11x12⋮x1px21x22⋮x2p⋯⋯⋱⋯xi1xi2⋮xip⎦⎥⎥⎥⎤
B = [ β 0 β 1 β 2 ⋯ β p ] B= \begin{bmatrix} \beta_0& \beta_1 & \beta_2& \cdots& \beta_p \end{bmatrix} B=[β0β1β2⋯βp], X = [ 1 1 1 ⋯ 1 x 11 x 21 x 31 ⋯ x i 1 x 12 x 22 x 32 ⋯ x i 2 ⋮ ⋮ ⋮ ⋱ ⋮ x 1 p x 2 p x 3 p ⋯ x i p ] X= \begin{bmatrix} 1&1&1&\cdots&1\\ x_{11} &x_{21}&x_{31}&\cdots&x_{i1} \\ x_{12} &x_{22}&x_{32}&\cdots&x_{i2} \\ \vdots&\vdots&\vdots&\ddots&\vdots&\\ x_{1p} &x_{2p}&x_{3p}&\cdots&x_{ip} \\ \end{bmatrix} X=⎣⎢⎢⎢⎢⎢⎡1x11x12⋮x1p1x21x22⋮x2p1x31x32⋮x3p⋯⋯⋯⋱⋯1xi1xi2⋮xip⎦⎥⎥⎥⎥⎥⎤
2.2 多元线性回归损失函数
- 仿照一元线性回归的损失函数, Q = ∑ 1 n ( y i − y i ^ ) 2 = ∑ 1 n ( y i − ( β 0 ^ + β 1 ^ x ) ) 2 Q=\sum\limits_1^n(y_i-\hat{y_i})^2=\sum\limits_1^n(y_i-(\hat{\beta_0}+\hat{\beta_1}x))^2 Q=1∑n(yi−yi^)2=1∑n(yi−(β0^+β1^x))2。从而推出多元线性回归的损失函数(向量表示, 其中 y = y ⃗ y=\vec{y} y=y)是个向量:
Q = ( y − y ^ ) T ( y − y ^ ) = ( y − β i x i ) T ( y − β i x i ) Q=(y-\hat{y})^T(y-\hat{y})=(y-\beta_ix_i)^T(y-\beta_ix_i) Q=(y−y^)T(y−y^)=(y−βixi)T(y−βixi)
2.3 对线性回归模型
我们现在把模型公式来做个总结,把线性回归模型简写为: y = β T x + β 0 y=\beta^Tx+\beta_0 y=βTx+β0
我们用矩阵来计算的时候,都是把 β 0 \beta_0 β0合并到 β \beta β矩阵中(同时在x样本矩阵的属性中全部加上1)。
其通过训练样本得出最优的 β \beta β和 β 0 \beta_0 β0(或者说,只用求 β \beta β矩阵中所有的值),从而对给定的新的样本x进行值y的预测,其实际上是在试图让模型预测值 β T x + β 0 \beta^Tx+\beta_0 βTx+β0 不断逼近真实值 y y y。
那我们是否可令模型预测值 β T x + β 0 \beta^Tx+\beta_0 βTx+β0 不断逼近真实值 y y y的”衍生物“呢?比如说, 现在真实值 y y y 扩大为指数族中的任一分布。
那就可将预测值的对数作为线性模型逼近的目标,这样得到的模型称为“对数线性回归”: l n y = β T x + β 0 ln y=\beta^Tx+\beta_0 lny=βTx+β0。它实际上是在试图让模型预测值 e β T x + β 0 e^{\beta^Tx+\beta_0} eβTx+β0断逼近真实值 y y y。
它形式上仍是线性回归,但实质上已是在求取输入空间到输出空间的非线性函数映射。这里的对数起到了将线性回归模型的预测值与真实标记联系起来的作用
多元线性回归暂且了解到这里。后面随着学习的加深会继续回头补充该文档。
2.4 广义线性模型
我们可以变换上面的”对数线性回归“公式为 y = e β T x + β 0 y=e^{\beta^Tx+\beta_0} y=eβTx+β0
但若真实值 y y y不为指数族中的分布,而变为更一般的分布呢?
这样得到的模型,我们称为*“广义线性模型”*: y = g − 1 ( β T x + β 0 ) y=g^{-1}(\beta^Tx+\beta_0) y=g−1(βTx+β0) 。
其中,函数 g ( ⋅ ) g(·) g(⋅)称为”联系函数“,其单调可微。
很显然,对数线性回归是广义线性模型在 g ( ⋅ ) = l n ( ⋅ ) g(·)=ln(·) g(⋅)=ln(⋅)时的特例。
3 逻辑回归(LR)
3.1 什么是逻辑回归?
- 前面说了,线性回归算法就是用来预测连续变量的。逻辑回归是用来做分类的一个分类模型。上面线性回归算法形式是Y=aX+b,y的取值范围值[ − ∞ , + ∞ -\infty ,+ \infty −∞,+∞]。有那么多取值,怎么进行分类呢?这个时候,我们把Y的结果带入到一个非线性变换的函数中就能得到[0,1]之间的取值范围了。这个函数叫Sigmoid函数。如设置一个阈值,就能实现分类了。其实并不难对不对?
用我自己的话来说,逻辑回归模型,就是将预测连续变量的模型给他转换成分类模型(离散的预测),有点像二维坐标中的连续曲线,给他分段, 一段一个分类的意思。
3.2 什么是Sigmoid函数?
Sigmoid函数公式:
S ( t ) = 1 1 + e − t S(t)=\frac{1}{1+e^{-t}} S(t)=1+e−t1

函数中t无论取什么值,其结果都在[0,-1]的区间内,回想一下,一个分类问题就有两种答案,一种是“是”,一种是“否”,那0对应着“否”,1对应着“是”,那又有人问了,你这不是[0,1]的区间吗,怎么会只有0和1呢?这个问题问得好,我们假设分类的阈值是0.5,那么超过0.5的归为1分类,低于0.5的归为0分类,阈值是可以自己设定的。
现在,最重要的地方来了。把线性回归 aX+b带入到t中就能得到我们的逻辑回归的一般模型方程:
H ( a , b ) = 1 1 + e ( a X + b ) H(a,b)=\frac{1}{1+e^{(aX+b)}} H(a,b)=1+e(aX+b)1
结果也可以理解成概率,换句话说,概率大于0.5,属于1分类。概率小于0.5的属于0分类,这就达到了分类的目的。
3.3 逻辑回归的损失函数
逻辑回归的损失函数是log loss,也就是对数似然函数,函数如下:
C o s t ( h θ ( x ) , y ) = { − l o g ( h θ ( x ) ) if y=1 − l o g ( 1 − h θ ( x ) ) if y=0 Cost(h_\theta(x),y)= \begin{cases} -log(h_\theta(x))&\text{if y=1}\\ -log(1-h_\theta(x))&\text{if y=0} \end{cases} Cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x))if y=1if y=0
公式中的 y=1 表示的是真实值为1时用第一个公式,真实 y=0 用第二个公式计算损失。为什么要加上log函数呢?可以试想一下,当真实样本为1是,但h=0概率,那么log0=∞,这就对模型最大的惩罚力度;当h=1时,那么log1=0,相当于没有惩罚,也就是没有损失,达到最优结果。所以数学家就想出了用log函数来表示损失函数。
h θ h_\theta hθ是预测值,是个概率,零点几;y是真实值,二分类中,真实值要么0,要么1,一元线性回归模型损失函数是 残差平方和。
最后按照梯度下降法一样,求解极小值点,得到想要的模型效果。
3.4 使用逻辑回归进行分类预测(demo)
参考阿里云平台的天池计算资源
操作步骤如下:
Step1:库函数导入
## 基础函数库
import numpy as np
## 导入画图库
import matplotlib.pyplot as plt
import seaborn as sns
## 导入逻辑回归模型函数
from sklearn.linear_model import LogisticRegression
Step2:训练模型
##Demo演示LogisticRegression分类
## 构造数据集
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]])
y_label = np.array([0, 0, 0, 1, 1, 1])
## 调用逻辑回归模型
lr_clf = LogisticRegression()
## 用逻辑回归模型拟合构造的数据集
lr_clf = lr_clf.fit(x_fearures, y_label) #其拟合方程为 y=w0+w1*x1+w2*x2
Step3:模型参数
##查看其对应模型的w,向量,包含两个值
print('the weight of Logistic Regression:',lr_clf.coef_)
##查看其对应模型的w0
print('the intercept(w0) of Logistic Regression:',lr_clf.intercept_)
##the weight of Logistic Regression:[[0.73462087 0.6947908]]
##the intercept(w0) of Logistic Regression:[-0.03643213]
Step4:数据和模型可视化
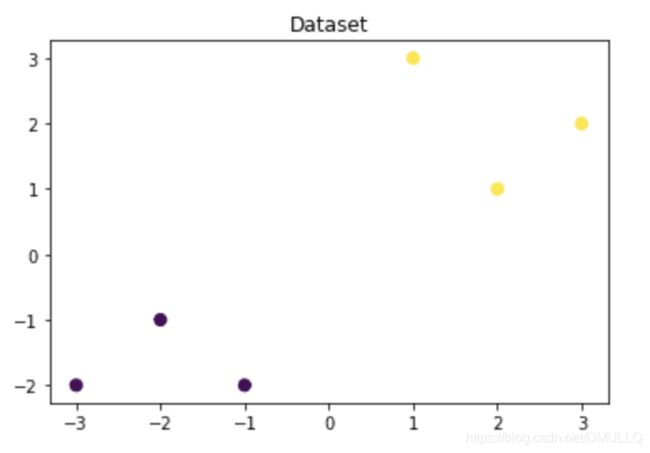
## 可视化构造的数据样本点
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
plt.show()
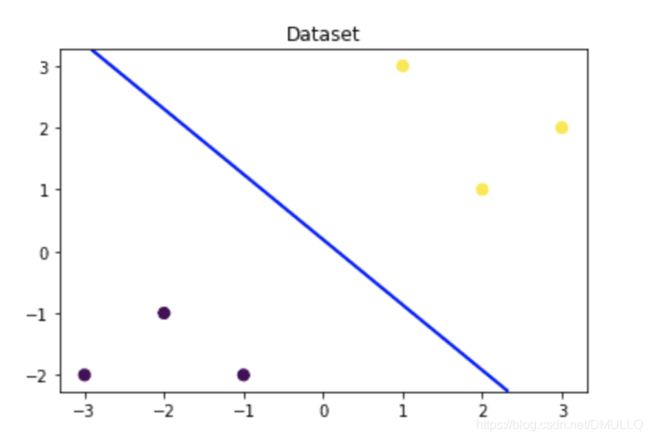
# 可视化决策边界
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
nx, ny = 200, 100
x_min, x_max = plt.xlim()
y_min, y_max = plt.ylim()
x_grid, y_grid = np.meshgrid(np.linspace(x_min, x_max, nx),np.linspace(y_min, y_max, ny))
z_proba = lr_clf.predict_proba(np.c_[x_grid.ravel(), y_grid.ravel()])
z_proba = z_proba[:, 1].reshape(x_grid.shape)
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')
plt.show()
### 可视化预测新样本
plt.figure()
## new point 1
x_fearures_new1 = np.array([[0, -1]])
plt.scatter(x_fearures_new1[:,0],x_fearures_new1[:,1], s=50, cmap='viridis')
plt.annotate(s='New point 1',xy=(0,-1),xytext=(-2,0),color='blue',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
## new point 2
x_fearures_new2 = np.array([[1, 2]])
plt.scatter(x_fearures_new2[:,0],x_fearures_new2[:,1], s=50, cmap='viridis')
plt.annotate(s='New point 2',xy=(1,2),xytext=(-1.5,2.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
## 训练样本
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
# 可视化决策边界
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')
plt.show()
Step5:模型预测
##在训练集和测试集上分布利用训练好的模型进行预测
y_label_new1_predict=lr_clf.predict(x_fearures_new1)
y_label_new2_predict=lr_clf.predict(x_fearures_new2)
print('The New point 1 predict class:\n',y_label_new1_predict)
print('The New point 2 predict class:\n',y_label_new2_predict)
##由于逻辑回归模型是概率预测模型(前文介绍的p = p(y=1|x,\theta)),所有我们可以利用predict_proba函数预测其概率
y_label_new1_predict_proba=lr_clf.predict_proba(x_fearures_new1)
y_label_new2_predict_proba=lr_clf.predict_proba(x_fearures_new2)
print('The New point 1 predict Probability of each class:\n',y_label_new1_predict_proba)
print('The New point 2 predict Probability of each class:\n',y_label_new2_predict_proba)
##TheNewpoint1predictclass:
##[0]
##TheNewpoint2predictclass:
##[1]
##TheNewpoint1predictProbabilityofeachclass:
##[[0.695677240.30432276]]
##TheNewpoint2predictProbabilityofeachclass:
##[[0.119839360.88016064]]