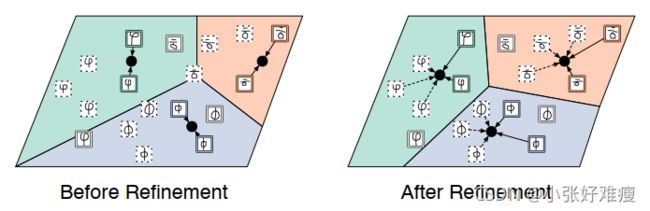
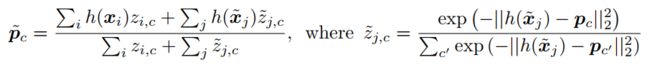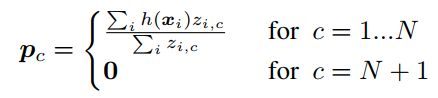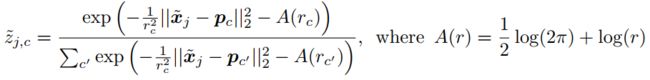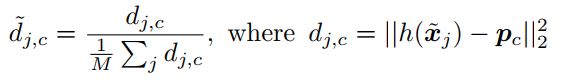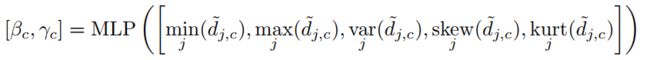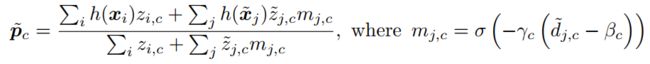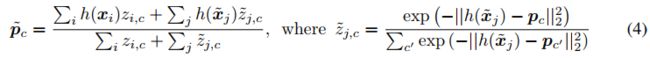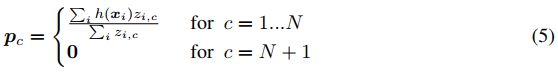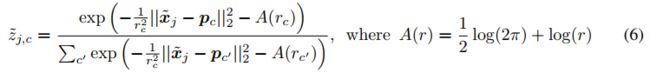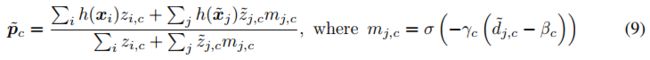【论文总结】Meta-Learning for semi-supervised few-shot classification(附翻译)

Meta-Learning for semi-supervised few-shot classification  半监督小样本分类的元学习

论文地址：https://arxiv.org/pdf/1803.00676.pdf

代码地址：https://github.com/renmengye/few-shot-ssl-public

思路：通过一个原型网络提取特征后，对特征进行聚类得到聚类中心，测试时按照距离来归类样本即可。在现实世界中，实际的小样本分类问题应该是只有少量已标注好的样本和很多未标注的样本，这些未标注的样本中有和已标注样本同类别的，也有不同类别的，因此需要半监督来进行小样本学习。

①带soft k-means的原型网络

soft k-means，即聚类后得到的是一个概率值，而hard k-means得到的是0,1。0表示不属于这个类，1表示属于这个类。

该方法适用于所有未标记的样本都属于已标记的样本中的一类，即没有未出现的类别。首先利用原先的原型为每个无标记数据分配一个属于各个类别的概率。然后在计算提炼后的新的原型的时候把这一概率考虑进去。

② Soft-means with a Distractor Cluster的原型网络

由于无标注样本集合R中一些样本真实类别并没有出现在集合S中，这类样本被称作distractor class。为了防止此类干扰项损害后面的预测推断过程以及提炼过程。我们假设干扰项的簇以原点为中心：

即有标记样本中由N个类，干扰类属于第N+1个类别。

然后需要学习一个距离尺度，此距离尺度对于N个已知类来说默认为1，不需要学，第N+1个类需要学习，可以认为这个距离尺度就是将所有干扰类里的样本拉向原点，让它们距离原点更近。

 ③使用mask和soft k-means的原型网络

在现实场景中，上述认为其他未出现过的类别属于同一个类是不合理的，因此仍然需要改进。

首先，计算样本与原型pc的归一化距离：

然后通过向MLP反馈原型归一化距离的各种统计数据，为每个原型预测阈值和斜率：

聚类中心的更新公式 ：

---

Abstract

In few-shot classification, we are interested in learning algorithms that train a classifier from only a handful of labeled examples. Recent progress in few-shot classification has featured meta-learning, in which a parameterized model for a learning algorithm is defined and trained on episodes representing different classification problems, each with a small labeled training set and its corresponding test set. In this work, we advance this few-shot classification paradigm towards a scenario where unlabeled examples are also available within each episode. We consider two situations: one where all unlabeled examples are assumed to belong to the same set of classes as the labeled examples of the episode, as well as the more challenging situation where  examples from other distractor classes are also provided. To address this paradigm, we propose novel extensions of Prototypical Networks (Snell et al., 2017) that are augmented with the ability to use unlabeled examples when producing prototypes. These modelsare trained in an end-to- end way on episodes, to learn to leverage the unlabeled examples successfully. We evaluate these methods on versions of the Omniglot and miniImageNet benchmarks, adapted to this new framework augmented with unlabeled examples. We also propose a new split of ImageNet, consisting of a large set of classes, with a hierarchical structure. Our experiments confirm that our Prototypical Networks can learn to improve their predictions due to unlabeled examples, much like a semi-supervised algorithm would.

在小样本分类中，我们感兴趣的是学习算法，这些算法只从少数几个标记的示例中训练分类器。小样本分类的最新进展以元学习为特征，其中定义了学习算法的参数化模型，并对代表不同分类问题的episode进行训练，每个episode都有一个小的标记训练集及其相应的测试集。在这项工作中，我们将这一小样本分类范式推进到一个场景中，在该场景中，未标记的示例在每一episode中也可用。我们考虑两种情况：一种假设所有未标记的实例属于同一组类，作为事件的标记实例，以及更具挑战性的情况，艺龙网还提供来自其他分心类的例子。为了解决这一范式，我们提出了原型网络的新扩展（Snell等人，2017年），该扩展增强了在生产原型时使用未标记示例的能力。这些模型以端到端的方式对episodes进行训练，以学习如何成功地利用未标记的示例。我们在Omniglot和miniImageNet基准测试的版本上评估这些方法，这些基准测试适应了这个新框架，并添加了未标记的示例。我们还提出了一种新的ImageNet拆分，它由一大组具有层次结构的类组成。我们的实验证实，由于未标记的示例，我们的原型网络可以学习改进其预测，就像半监督算法一样。

1 Introduction

The availability of large quantities of labeled data has enabled deep learning methods to achieve impressive breakthroughs in several tasks related to artificial intelligence, such as speech recognition, object recognition and machine translation. However, current deep learning approaches struggle in tackling problems for which labeled data are scarce. Specifically, while current methods excel at tackling a single problem with lots of labeled data, methods that can simultaneously solve a large variety of problems that each have only a few labels are lacking. Humans on the other hand are readily able to rapidly learn new classes, such as new types of fruit when we visit a tropical country. This significant gap between human and machine learning provides fertile ground for deep learning developments.

大量标记数据的可用性使深度学习方法能够在与人工智能相关的若干任务中取得令人印象深刻的突破，如语音识别、目标识别和机器翻译。然而，当前的深度学习方法在解决标记数据稀缺的问题时遇到了困难。具体地说，虽然当前的方法擅长处理带有大量标记数据的单个问题，但缺乏能够同时解决各种各样的问题（每个问题只有几个标记）的方法。另一方面，当我们访问一个热带国家时，人类能够很快地学习新的类别，例如新的水果类型。人类和机器学习之间的巨大差距对深入学习的发展起到了推动作用。

For this reason, recently there has been an increasing body of work on few-shot learning, which
considers the design of learning algorithms that specifically allow for better generalization on problems with small labeled training sets. Here we focus on the case of few-shot classification, where the given classification problem is assumed to contain only a handful of labeled examples per class. One approach to few-shot learning follows a form of meta-learning 1 (Thrun, 1998; Hochreiter et al., 2001), which performs transfer learning from a pool of various classification problems generated from large quantities of available labeled data, to new classification problems from classes unseen at training time. Meta-learning may take the form of learning a shared metric (Vinyals et al., 2016; Snell et al., 2017), a common initialization for few-shot classifiers (Ravi & Larochelle, 2017; Finn et al., 2017) or a generic inference network (Santoro et al., 2016; Mishra et al., 2017).

出于这个原因，最近有越来越多的关于小样本学习的工作，其中考虑了学习算法的设计，特别是允许更好地泛化小标记训练集的问题。在这里，我们将重点放在小样本分类的情况下，假设给定的分类问题每个类只包含少数几个标记的示例。小样本学习的一种方法是元学习（Thrun，1998；Hochreiter et al.，2001），它从大量可用的标记数据生成的各种分类问题库中执行迁移学习，从训练时看不到的类中执行新的分类问题。元学习可以采取学习共享度量（Vinyals等人，2016；Snell等人，2017）、小样本的通用初始化分类器（Ravi&Larochelle，2017；Finn等人，2017）或通用推理网络（Santoro等人，2016；Mishra等人，2017）的形式。

These various meta-learning formulations have led to significant progress recently in few-shot classification. However, this progress has been limited in the setup of each few-shot learning episode, which differs from how humans learn new concepts in many dimensions. In this paper we aim to generalize the setup in two ways. First, we consider a scenario where the new classes are learned in the presence of additional unlabeled data. While there have been many successful applications of semisupervised learning to the regular setting of a single classification task (Chapelle et al., 2010) where classes at training and test time are the same, such work has not addressed the challenge of performing transfer to new classes never seen at training time, which we consider here. Second, we consider the situation where the new classes to be learned are not viewed in isolation. Instead, many of the unlabeled examples are from different classes; the presence of such distractor classes introduces an additional and more realistic level of difficulty to the fewshot problem.

这些不同的元学习公式最近在小样本分类方面取得了重大进展。然而，这一进展在小样本学习的设置中都受到限制，这与人类在许多方面学习新概念的方式不同。在本文中，我们的目标是从两个方面概括设置。首先，我们考虑在附加的未标记数据的存在下学习新类的场景。尽管半监督学习已经成功应用到单一分类任务（Chanelet等人，2010）的常规设置，其中训练和测试时的类相同，但是我们认为此类工作并没有解决执行转移到训练时从未见过的新类的场景。第二，我们考虑的情况下，要学习的新类不是孤立地看待。相反，许多未标记的示例来自不同的类别；这种干扰类的存在给小样本问题带来了更大的难度。

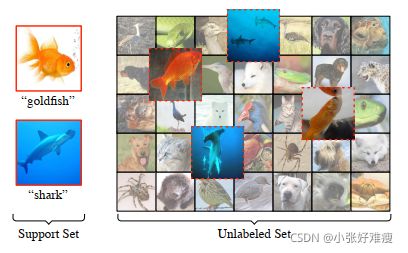
Figure 1: Consider a setup where the aim is to learn a classifier to distinguish between two previously unseen classes, goldfish and shark, given not only labeled examples of these two classes, but also a larger pool of unlabeled examples, some of which may belong to one of these two classes of interest. In this work we aim to move a step closer to this more natural learning framework by incorporating in our learning episodes unlabeled data from the classes we aim to learn representations for (shown with dashed red borders) as well as from distractor classes .考虑到目的是学习一个分类器来区分两个以前看不见的类，金鱼和鲨鱼，不仅给出了这两个类的标记实例，而且还提供了一个未标记的更大的数据池，其中一些可能属于这两个类中的一个。在这项工作中，我们的目标是通过在我们的学习片段中加入来自我们旨在学习表征的类别（用红色虚线显示）以及分心者班级的未标记数据，向更自然的学习框架迈进一步。

This work is a first study of this challenging semi-supervised form of few-shot learning. First, we define the problem and propose benchmarks for evaluation that are adapted from the Omniglot and miniImageNet benchmarks used in ordinary few-shot learning. We perform an extensive empirical investigation of the two settings mentioned above, with and without distractor classes. Second, we propose and study three novel extensions of Prototypical Networks (Snell et al., 2017), a state-ofthe-art approach to few-shot learning, to the semi-supervised setting. Finally, we demonstrate in our experiments that our semi-supervised variants successfully learn to leverage unlabeled examples and outperform purely supervised Prototypical Networks.

这项工作是第一次研究这种具有挑战性的半监督形式的小样本学习。首先，我们定义了问题并提出了评估基准，这些基准改编自Omniglot和miniImageNet基准，用于普通的小样本学习。我们对上面提到的两种场景进行了广泛的实证调查，有无干扰类别。其次，我们提出并研究了原型网络的三个新扩展（Snell et al.，2017），这是一种最先进的小样本学习方法，适用于半监督环境。最后，我们在实验中证明，我们的半监督变体成功地学习利用未标记的示例，并优于纯监督原型网络。

2  Background

We start by defining precisely the current paradigm for few-shot learning and the Prototypical Network approach to this problem.

首先，我们精确地定义了当前小样本学习的范例以及解决这个问题的典型网络方法。

2.1 Few-shot Learning

Recent progress on few-shot learning has been made possible by following an episodic paradigm. Consider a situation where we have a large labeled dataset for a set of classes Ctrain. However, after training on examples from Ctrain, our ultimate goal is to produce classifiers for a disjoint set of new classes Ctest, for which only a few labeled examples will be available. The idea behind the episodic paradigm is to simulate the types of few-shot problems that will be encountered at test, taking advantage of the large quantities of available labeled data for classes Ctrain.

最近，小样本学习的进展是通过遵循一种情景范式而实现的。考虑一个情况，我们为一组类Ctrain有一个很大的标记数据集。然而，在对来自Ctrain的示例进行训练后，我们的最终目标是为一组不相交的新类Ctest生成分类器，对于这些类，只有少数标记的示例可用。幕式范例背后的思想是模拟测试中将遇到的小样本问题的类型，利用类Ctrain的大量可用标记数据。

Specifically, models are trained on K-shot, N-way episodes constructed by first sampling a small subset of N classes from Ctrain and then generating: 1) a training (support) set S =
containing K examples from each of the N classes and  2) a test (query) set of different examples from the same N classes. Each xi ∈ RD is an input vector of dimension D and yi ∈ {1,2,..., N} is a class label (similarly for 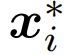and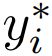). Training on such episodes is done by feeding the support set S to the model and updating its parameters to minimize the loss of its predictions for the examples in the query set Q.

​具体地说，通过首先从Ctrain中抽取N个类的一小部分样本，然后生成：1）训练（支持）集S=包含N个类中每个类的K个示例，以及2）相同N个类中不同示例的测试（查询）集，对模型进行K-shot、N-way集训练。每xi∈ RD是维数为D和yi的输入向量yi∈{1,2，…，N}是一个类标签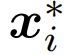（与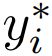类似）。通过将支持集S提供给模型并更新其参数以最小化其对查询集Q中的示例的预测损失，可以对此类事件进行训练。
​
One way to think of this approach is that our model effectively trains to be a good learning algorithm. Indeed, much like a learning algorithm, the model must take in a set of labeled examples and produce a predictor that can be applied to new examples. Moreover, training directly encourages the classifier produced by the model to have good generalization on the new examples of the query set. Due to this analogy, training under this paradigm is often referred to as learning to learn or meta-learning.

考虑这种方法的一个方法是，我们的模型有效地训练成为一个好的学习算法。事实上，与学习算法非常相似，该模型必须接受一组标记的示例，并生成可应用于新示例的预测值。此外，训练直接鼓励模型生成的分类器在查询集的新示例上具有良好的泛化能力。基于这种类比，这种范式下的培训通常被称为“学会学习”或“元学习”。

On the other hand, referring to the content of episodes as training and test sets and to the process of learning on these episodes as meta-learning or meta-training (as is sometimes done in the literature) can be confusing. So for the sake of clarity, we will refer to the content of episodes as support and query sets, and to the process of iterating over the training episodes simply as training.

另一方面，将episodes的内容称为训练集和测试集，将这些episodes的学习过程称为元学习或元训练（文献中有时会这样做）可能会令人困惑。因此，为了清晰起见，我们将片段的内容称为支持集和查询集，并将迭代训练片段的过程称为训练。 

2.2 Prototypical Networks

Prototypical Network (Snell et al., 2017) is a few-shot learning model that has the virtue of being simple and yet obtaining state-of-the-art performance. At a high-level, it uses the support set S to extract a prototype vector from each class, and classifies the inputs in the query set based on their distance to the prototype of each class. More precisely, Prototypical Networks learn an embedding function h(x), parameterized as a neural network, that maps examples into a space where examples from the same class are close and those from different classes are far. All parameters of Prototypical Networks lie in the embedding function. To compute the prototype pc of each class c, a per-class average of the embedded examples is performed:

原型网络（Snell等人，2017年）是一种小样本学习模型，其优点是简单且可获得最先进的性能。在高层，它使用支持集S从每个类中提取原型向量，并根据输入到每个类原型的距离对查询集中的输入进行分类。更准确地说，原型网络学习一个嵌入函数h（x），被参数化为一个神经网络，它将示例映射到一个空间中，其中来自同一类的示例比较接近，而来自不同类的示例比较远。原型网络的所有参数都在嵌入函数中。为了计算每个c类的原型pc，执行嵌入式示例的每类平均值：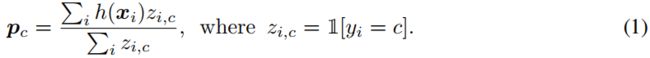

These prototypes define a predictor for the class of any new (query) example x∗, which assigns a probability over any class c based on the distances between x∗ and each prototype, as follows:

这些原型为任何新（查询）示例x的类定义了一个预测器∗, 根据x和x之间的距离，在任何c类上分配一个概率∗ 以及每个原型，如下所示：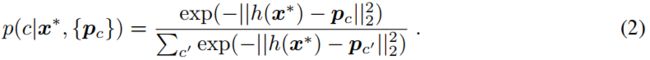

The loss function used to update Prototypical Networks for a given training episode is then simply the average negative log-probability of the correct class assignments, for all query examples:

对于所有查询示例，用于更新给定训练集的原型网络的损失函数仅为正确类别分配的平均负对数概率：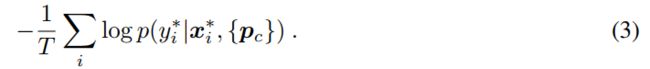

Training proceeds by minimizing the average loss, iterating over training episodes and performing a gradient descent update for each.

训练通过最小化平均损失、迭代训练事件并对每个事件执行梯度下降更新来进行。

Generalization performance is measured on test set episodes, which contain images from classes in Ctest instead of Ctrain. For each test episode, we use the predictor produced by the Prototypical Network for the provided support set S to classify each of query input x∗ into the most likely class .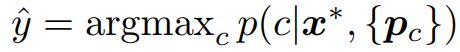

泛化性能是在测试集集集上测量的，其中包含来自Ctest中的类而不是Ctrain中的类的图像。对于每个测试集，我们使用原型网络为支持集S生成的预测器对每个查询输入进行分类，得到最可能的类别。 

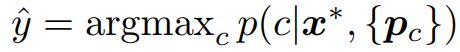3 Semi-supervised Few-shot Learninig

We now define the semi-supervised setting considered in this work for few-shot learning.

现在，我们定义了这项工作中考虑的用于小样本学习的半监督设置。

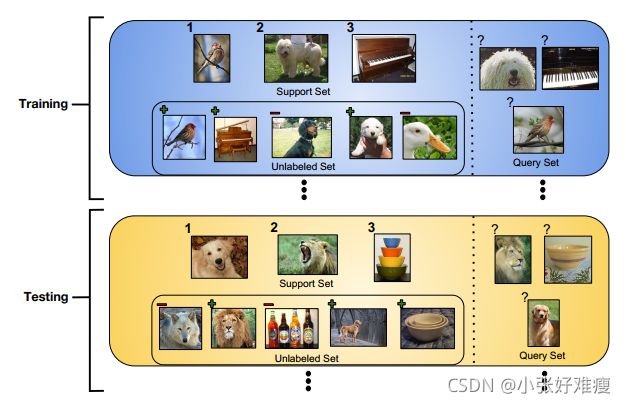
The training set is denoted as a tuple of labeled and unlabeled examples: (S; R). The labeled portion is the usual support set S of the few-shot learning literature, containing a list of tuples of inputs and targets. In addition to classic few-shot learning, we introduce an unlabeled set R containing only inputs: 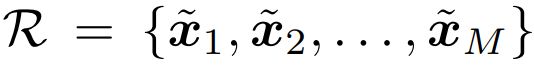. As in the purely supervised setting, our models are trained to perform well when predicting the labels for the examples in the episode’s query set Q. Figure 2 shows a visualization of training and test episodes.

训练集表示为有标记和无标记示例的元组：（S；R）。标记部分是小样本学习文献中的常用支持集，包含输入和目标的元组列表。除了经典的小样本学习外，我们还引入了一个只包含输入的未标记集R: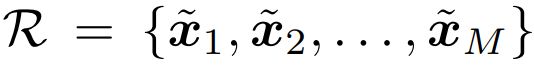。与纯监督设置一样，我们的模型经过训练，在预测事件查询集Q中示例的标签时表现良好。图2显示了训练和测试事件的可视化。

Figure 2: Example of the semi-supervised few-shot learning setup. Training involves iterating through training episodes, consisting of a support set S, an unlabeled set R, and a query set Q. The goal is to use the labeled items (shown with their numeric class label) in S and the unlabeled items in R within each episode to generalize to good performance on the corresponding query set. The unlabeled items in R may either be pertinent to the classes we are considering (shown above with green plus signs) or they may be distractor items which belong to a class that is not relevant to the current episode (shown with red minus signs). However note that the model does not actually have ground truth information as to whether each unlabeled example is a distractor or not; the plus/minus signs are shown only for illustrative purposes. At test time, we are given new episodes consisting of novel classes not seen during training that we use to evaluate the meta-learning method.

半监督小样本学习设置示例。训练涉及迭代训练集，包括支持集S、未标记集R和查询集Q。目标是在每个集内使用S中的标记项（显示其数字类标签）和R中的未标记项，以在相应的查询集上获得良好的性能。R中未标记的项目可能与我们正在考虑的类别相关（上面用绿色加号显示），也可能是属于与当前事件无关的类别的干扰项目（用红色减号显示）。但是请注意，该模型实际上没有关于每个未标记示例是否为干扰因素的基本事实信息；显示加号/减号仅用于说明目的。在测试时，我们会看到一些新的类别，这些类别在我们用来评估元学习方法的训练中没有出现。

3.1 Semi-supervised Prototypical Networks

In their original formulation, Prototypical Networks do not specify a way to leverage the unlabeled set R. In what follows, we now propose various extensions that start from the basic definition of prototypes pc and provide a procedure for producing refined prototypes using the unlabeled examples in R.

在其原始公式中，原型网络没有指定利用未标记集R的方法。在下文中，我们提出了各种扩展，从原型pc的基本定义开始，并提供了使用R中的未标记示例生成细化原型p~c的过程。

After the refined prototypes are obtained, each of these models is trained with the same loss function for ordinary Prototypical Networks of Equation 3, but replacing pc with . That is, each query example is classified into one of the N classes based on the proximity of its embedded position with the corresponding refined prototypes, and the average negative logprobability of the correct classification is used for training.

 ​在获得细化的原型后，对方程3中的普通原型网络，使用相同的损失函数对每个模型进行训练，但将pc替换为。也就是说，每个查询示例根据其嵌入位置与相应优化原型的接近程度被分类为N个类中的一个，并且使用正确分类的平均负对数概率进行训练。

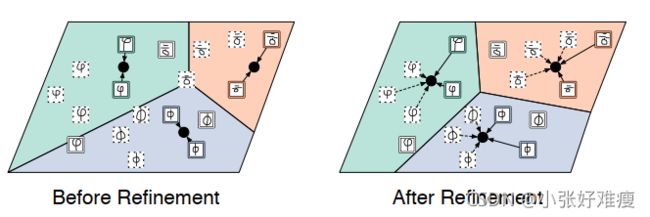
Figure 3: Left: The prototypes are initialized based on the mean location of the examples of the corresponding class, as in ordinary Prototypical Networks. Support, unlabeled, and query examples have solid, dashed, and white colored borders respectively. Right: The refined prototypes obtained by incorporating the unlabeled examples, which classifies all query examples correctly.  左：原型是根据相应类的示例的平均位置初始化的，就像在普通原型网络中一样。支持、未标记和查询示例分别具有实线、虚线和白色边框。右图：通过合并未标记的示例获得的细化原型，可以正确地对所有查询示例进行分类。

3.1.1 Prototypical Networks with Soft-means

We first consider a simple way of leveraging unlabeled examples for refining prototypes, by taking inspiration from semi-supervised clustering. Viewing each prototype as a cluster center, the refinement process could attempt to adjust the cluster locations to better fit the examples in both the support and unlabeled sets. Under this view, cluster assignments of the labeled examples in the support set are considered known and fixed to each example’s label. The refinement process must instead estimate the cluster assignments of the unlabeled examples and adjust the cluster locations (the prototypes) accordingly.

我们首先考虑一个简单的方法，利用未标记的例子来提炼原型，通过灵感来自半监督聚类。将每个原型视为集群中心，细化过程可以尝试调整集群位置，以更好地适应支持集和未标记集中的示例。在此视图下，支持集中已标记示例的集群分配被视为已知并固定到每个示例的标签上。精化过程必须评估未标记示例的集群分配，并相应地调整集群位置（原型）。

One natural choice would be to borrow from the inference performed by soft k-means. We prefer this version of k-means over hard assignments since hard assignments would make the inference non-differentiable. We start with the regular Prototypical Network’s prototypes pc (as specified in Equation 1) as the cluster locations. Then, the unlabeled examples get a partial assignment (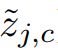) to each cluster based on their Euclidean distance to the cluster locations. Finally, refined prototypes are obtained by incorporating these unlabeled examples.

一个自然的选择是借用soft k-means进行的推理。我们更喜欢这个版本的k-means而不是硬赋值，因为硬赋值会使推理不可微。我们从常规原型网络的原型pc（如等式1所示）开始，作为集群位置。然后，未标记的示例根据其到簇位置的欧几里德距离对每个簇进行部分赋值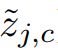（）。最后，通过合并这些未标记的示例，可以获得细化的原型。

This process can be summarized as follows: 这一过程可概括如下：

Predictions of each query input’s class is then modeled as in Equation 2, but using the refined prototypes .

然后，对每个查询输入类的预测进行建模，如方程2所示，但使用改进的原型。

We could perform several iterations of refinement, as is usual in k-means. However, we have experimented with various number of iterations and found results to not improve beyond a single refinement step.

我们可以像k-means中通常的那样执行多次细化迭代。然而，我们已经对不同数量的迭代进行了实验，发现结果并没有超过一个细化步骤。

3.1.2 Prototypical Networks with Soft-means with a Distractor Cluster

The soft k-means approach described above implicitly assumes that each unlabeled example belongs to either one of the N classes in the episode. However, it would be much more general to not make that assumption and have a model robust to the existence of examples from other classes, which we refer to as distractor classes. For example, such a situation would arise if we wanted to distinguish between pictures of unicycles and scooters, and decided to add an unlabeled set by downloading images from the web. It then would not be realistic to assume that all these images are of unicycles or scooters. Even with a focused search, some may be from similar classes, such as bicycle.

上面描述的soft k-means方法隐含地假设每个未标记的示例属于事件中的N个类中的任意一个。然而，更一般的做法是不做这样的假设，而是有一个对其他类（我们称之为干扰物类）示例的存在具有鲁棒性的模型。例如，如果我们想要区分独轮车和滑板车的图片，并决定通过从网页下载图像来添加未标记的集合，就会出现这种情况。因此，假设所有这些图像都是独轮车或滑板车的图像是不现实的。即使是有重点的搜索，有些可能来自类似的类别，比如自行车。

Since soft k-means distributes its soft assignments across all classes, distractor items could be harmful and interfere with the refinement process, as prototypes would be adjusted to also partially account for these distractors. A simple way to address this is to add an additional cluster whose purpose is to capture the distractors, thus preventing them from polluting the clusters of the classes of interest:

由于soft k-means将其软赋值分布在所有类中，干扰项可能是有害的，并干扰细化过程，因为原型也会被调整以部分解释这些干扰项。解决这个问题的一个简单方法是添加一个额外的集群，其目的是捕获干扰物，从而防止它们干扰感兴趣类别的集群：

Here we take the simplifying assumption that the distractor cluster has a prototype centered at the origin. We also consider introducing length-scales rc to represent variations in the within-cluster  sdistances, specifically for the distractor cluster:

在这里，我们采用简化的假设，即干扰集群有一个以原点为中心的原型。我们还考虑引入长度尺度rc来表示簇内距离的变化，特别是对于分心器簇：

 For simplicity, we set r1...N to 1 in our experiments, and only learn the length-scale of the distractor cluster rN+1.

为了简单起见，我们在实验中将r1...N设置为1，并且只学习干扰簇rN+1的长度尺度。

3.1.3 Prototypical Networks with Soft-means and Masking

Modeling distractor unlabeled examples with a single cluster is likely too simplistic. Indeed, it is inconsistent with our assumption that each cluster corresponds to one class, since distractor examples may very well cover more than a single natural object category. Continuing with our unicycles and bicycles example, our web search for unlabeled images could accidentally include not only bicycles, but other related objects such as tricycles or cars. This was also reflected in our experiments, where we constructed the episode generating process so that it would sample distractor examples from multiple classes.

用单个集群建模干扰物未标记的示例可能过于简单。事实上，这与我们的假设是不一致的，即每个簇对应一个类，因为干扰物的例子很可能涵盖不止一个自然对象类别。继续我们的独轮车和自行车示例，我们对未标记图像的网页搜索可能不仅包括自行车，还包括其他相关目标，如三轮车或汽车。这也反映在我们的实验中，在实验中，我们构建了片段生成过程，以便从多个类别中抽取干扰者的例子。

To address this problem, we propose an improved variant: instead of capturing distractors with a high-variance catch-all cluster, we model distractors as examples that are not within some area of any of the legitimate class prototypes. This is done by incorporating a soft-masking mechanism on the contribution of unlabeled examples. At a high level, we want unlabeled examples that are closer to a prototype to be masked less than those that are farther.

为了解决这个问题，我们提出了一个改进的变体：我们不使用高方差的“捕获所有”聚类来捕获干扰物，而是将干扰物建模为不在任何合法类原型的某些区域内的示例。这是通过在未标记示例的贡献上加入soft-masking机制来实现的。在较高的层次上，我们希望与原型更接近的未标记示例比距离更远的示例更少被掩盖。

More specifically, we modify the soft k-means refinement as follows. We start by computing normalized distances 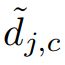between examples and prototypes pc:

更具体地说，我们修改soft k-means 细化如下。我们首先计算归一化距离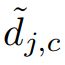在示例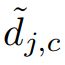和原型pc之间：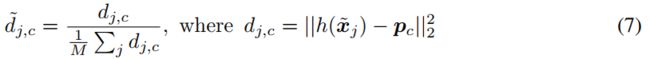

Then, soft thresholds βc and slopes γc are predicted for each prototype, by feeding to a small neural network various statistics of the normalized distances for the prototype:

然后，通过向小型神经网络提供原型归一化距离的各种统计信息，预测每个原型的软阈值βc和斜率γc：

This allows each threshold to use information on the amount of intra-cluster variation to determine how aggressively it should cut out unlabeled examples.

这需要每个阈值使用关于簇内变化量的信息来确定它应该以多大的力度删除未标记的示例。

Then, soft masks for the contribution of each example to each prototype are computed, by comparing to the threshold the normalized distances, as follows: 

然后，软掩模通过将标准化距离与阈值进行比较，计算每个示例对每个原型的贡献，如下所示：

 where σ(·) is the sigmoid function.

When training with this refinement process, the model can now use its MLP in Equation 8 to learn
to include or ignore entirely certain unlabeled examples. The use of soft masks makes this process entirely differentiable2. Finally, much like for regular soft k-means (with or without a distractor cluster), while we could recursively repeat the refinement for multiple steps, we found a single step to perform well enough.

当使用此细化过程进行训练时，模型现在可以使用等式8中的MLP来学习包含或忽略某些完全未标记的示例。soft masks 的使用使这一过程完全不同。最后，与常规soft k-means（带或不带干扰物集群）非常相似，虽然我们可以递归地重复多个步骤的细化，但我们发现一个步骤的性能足够好。

4 Related Work

We summarize here the most relevant work from the literature on few-shot learning, semi-supervised learning and clustering.

我们在这里总结了有关小样本学习、半监督学习和聚类的文献中最相关的工作。

The best performing methods for few-shot learning use the episodic training framework prescribed by meta-learning. The approach within which our work falls is that of metric learning methods. Previous work in metric-learning for few-shot-classification includes Deep Siamese Networks (Koch et al., 2015), Matching Networks (Vinyals et al., 2016), and Prototypical Networks (Snell et al., 2017), which is the model we extend to the semi-supervised setting in our work. The general idea here is to learn an embedding function that embeds examples belonging to the same class close together while keeping embeddings from separate classes far apart. Distances between embeddings of items from the support set and query set are then used as a notion of similarity to do classification. Lastly, closely related to our work with regard to extending the few-shot learning setting, Bachman et al. (2017) employ Matching Networks in an active learning framework where the model has a choice of which unlabeled item to add to the support set over a certain number of time steps before classifying the query set. Unlike our setting, their meta-learning agent can acquire ground-truth labels from the unlabeled set, and they do not use distractor examples.

小样本学习的最佳执行方法使用元学习规定的情景训练框架。我们的工作所采用的方法是度量学习方法。以前在小样本分类的度量学习方面的工作包括深暹罗网络（Koch等人，2015年）、匹配网络（Vinyals等人，2016年）和原型网络（Snell等人，2017年），这是我们在工作中扩展到半监督设置的模型。这里的总体思想是学习一个嵌入函数，该函数将属于同一类的示例紧密嵌入在一起，同时将来自不同类的嵌入保持在很远的距离。然后，将项目嵌入到支持集和查询集之间的距离作为相似性的概念进行分类。最后，Bachman等人（2017年）在主动学习框架中采用匹配网络，模型可以选择在一定数量的时间步内，在对查询集进行分类之前，将哪个未标记项添加到支持集，这与我们关于扩展小样本学习设置的工作密切相关。与我们的设置不同，他们的元学习代理可以从未标记的集合中获取ground truth标签，并且他们不使用干扰示例。

Other meta-learning approaches to few-shot learning include learning how to use the support set to update a learner model so as to generalize to the query set. Recent work has involved learning either the weight initialization and/or update step that is used by a learner neural network (Ravi & Larochelle, 2017; Finn et al., 2017). Another approach is to train a generic neural architecture such as a memory-augmented recurrent network (Santoro et al., 2016) or a temporal convolutional network (Mishra et al., 2017) to sequentially process the support set and perform accurate predictions of the labels of the query set examples. These other methods are also competitive for few-shot learning, but we chose to extend Prototypical Networks in this work for its simplicity and efficiency.

小样本学习的其他元学习方法包括学习如何使用支持集更新学习者模型，从而推广到查询集。最近的工作涉及学习者神经网络使用的权重初始化和/或更新步骤（Ravi&Larochelle，2017；Finn等人，2017）。另一种方法是训练一种通用的神经结构，如记忆增强的递归网络（Santoro等人，2016年）或时间卷积网络（Mishra等人，2017年），以顺序处理支持集并对查询集示例的标签进行准确预测。这些其他方法对于小样本学习也具有竞争力，但我们选择在这项工作中扩展原型网络，因为它简单高效。

As for the literature on semi-supervised learning, while it is quite vast (Zhu, 2005; Chapelle et al.,
2010), the most relevant category to our work is related to self-training (Yarowsky, 1995; Rosenberg et al., 2005). Here, a classifier is first trained on the initial training set. The classifier is then used to classify unlabeled items, and the most confidently predicted unlabeled items are added to the training set with the prediction of the classifier as the assumed label. This is similar to our soft k-Means extension to Prototypical Networks. Indeed, since the soft assignments (Equation 4) match the regular Prototypical Network’s classifier output for new inputs (Equation 2), then the refinement can be thought of re-feeding to a Prototypical Network a new support set augmented with (soft) self-labels from the unlabeled set.

至于关于半监督学习的文献，尽管它相当庞大（Zhu，2005；Chapelle等人，2010），但与我们工作最相关的类别是自我训练（Yarowsky，1995；Rosenberg等人，2005）。这里，首先在初始训练集上训练分类器。然后使用分类器对未标记项进行分类，并将最可靠地预测的未标记项添加到训练集中，分类器的预测作为假设标签。这类似于我们对原型网络的soft k-Means扩展。事实上，由于软分配（等式4）与常规原型网络的分类器输出相匹配以获得新输入（等式2），因此可以认为改进是向原型网络重新提供一个新的支持集，该支持集由未标记集的（软）自标签扩充。

Our algorithm is also related to transductive learning (Vapnik, 1998; Joachims, 1999; Fu et al., 2015), where the base classifier gets refined by seeing the unlabeled examples. In practice, one could use our method in a transductive setting where the unlabeled set is the same as the query set; however, here to avoid our model memorizing labels of the unlabeled set during the meta-learning procedure, we split out a separate unlabeled set that is different from the query set.

我们的算法也与转换学习相关（Vapnik，1998；Joachims，1999；Fu等人，2015），其中基本分类器通过查看未标记的示例进行细化。在实践中，我们可以在转换设置中使用我们的方法，其中未标记集与查询集相同；然而，为了避免我们的模型在元学习过程中记忆未标记集的标签，我们分离出一个不同于查询集的单独的未标记集。

In addition to the original k-Means method (Lloyd, 1982), the most related work to our setup involving clustering algorithms considers applying k-Means in the presence of outliers (Hautamäki et al., 2005; Chawla & Gionis, 2013; Gupta et al., 2017). The goal here is to correctly discover and ignore the outliers so that they do not wrongly shift the cluster locations to form a bad partition of the true data. This objective is also important in our setup as not ignoring outliers (or distractors) will wrongly shift the prototypes and negatively influence classification performance.

除了原始的k-means方法（Lloyd，1982），与我们的聚类算法设置最相关的工作考虑在存在异常值的情况下应用k-means（Hautamäki等人，2005年；Chawla&Gionis，2013年；Gupta等人，2017年）。这里的目标是正确地发现并忽略异常值，以便它们不会错误地移动集群位置，从而形成真实数据的坏分区。这一目标在我们的设置中也很重要，因为不忽略异常值（或干扰因素）将错误地改变原型并对分类性能产生负面影响。

Our contribution to the semi-supervised learning and clustering literature is to go beyond the classical setting of training and evaluating within a single dataset, and consider the setting where we must learn to transfer from a set of training classes Ctrain to a new set of test classes Ctest.

我们对半监督学习和聚类文献的贡献是超越一个单一的数据集内的训练和评估的经典设置，并考虑我们必须学会从一组训练类cSet转移到一组新的测试类cTest的设置。

5 EXPERIMENTS

5.1 DATASETS

We evaluate the performance of our model on three datasets: two benchmark few-shot classification datasets and a novel large-scale dataset that we hope will be useful for future few-shot learning work.

我们在三个数据集上评估了我们模型的性能：两个基准小样本分类数据集和一个新的大规模数据集，我们希望这将对未来的小样本学习工作有用。

Omniglot (Lake et al., 2011) is a dataset of 1,623 handwritten characters from 50 alphabets. Each
character was drawn by 20 human subjects. We follow the few-shot setting proposed by Vinyals
et al. (2016), in which the images are resized to 28 × 28 pixels and rotations in multiples of 90◦ are applied, yielding 6,492 classes in total. These are split into 4,112 training classes, 688 validation classes, and 1,692 testing classes.

Omniglot（Lake et al.，2011）是一个包含50个字母表中1623个手写字符的数据集。每个人物由20名受试者绘制。我们遵循Vinyals等人（2016）提出的少镜头设置，其中图像大小调整为28×28像素，旋转倍数为90◦ 已应用，共产生6492个类。这些课程分为4112个训练类、688个验证类和1692个测试类。

miniImageNet (Vinyals et al., 2016) is a modified version of the ILSVRC-12 dataset (Russakovsky et al., 2015), in which 600 images for each of 100 classes were randomly chosen to be part of the dataset. We rely on the class split used by Ravi & Larochelle (2017). These splits use 64 classes for training, 16 for validation, and 20 for test. All images are of size 84 × 84 pixels.

miniImageNet（Vinyals等人，2016年）是ILSVRC-12数据集（Russakovsky等人，2015年）的一个修改版本，其中随机选择了100个类别中每个类别的600张图像作为数据集的一部分。我们依靠Ravi&Larochelle（2017）使用的分类。这些拆分使用64个类进行培训，16个用于验证，20个用于测试。所有图像的大小均为84×84像素。

tieredImageNet is our proposed dataset for few-shot classification. Like miniImagenet, it is a subset of ILSVRC-12. However, tieredImageNet represents a larger subset of ILSVRC-12 (608 classes rather than 100 for miniImageNet). Analogous to Omniglot, in which characters are grouped into alphabets, tieredImageNet groups classes into broader categories corresponding to higher-level nodes in the ImageNet (Deng et al., 2009) hierarchy. There are 34 categories in total, with each category containing between 10 and 30 classes. These are split into 20 training, 6 validation and 8 testing categories (details of the dataset can be found in the supplementary material). This ensures that all of the training classes are sufficiently distinct from the testing classes, unlike miniImageNet and other alternatives such as randImageNet proposed by Vinyals et al. (2016). For example, “pipe organ” is a training class and “electric guitar” is a test class in the Ravi & Larochelle (2017) split of miniImagenet, even though they are both musical instruments. This scenario would not occur in tieredImageNet since “musical instrument” is a high-level category and as such is not split between training and test classes. This represents a more realistic few shot learning scenario since in general we cannot assume that test classes will be similar to those seen in training. Additionally, the tiered structure of tieredImageNet may be useful for few shot learning approaches that can take advantage of hierarchical relationships between classes. We leave such interesting extensions for future work.

tieredImageNet是我们提出的少数镜头分类数据集。与miniImagenet一样，它也是ILSVRC-12的一个子集。然而，tieredImageNet代表ILSVRC-12的一个较大子集（对于miniImageNet，608个类而不是100个类）。与Omniglot类似，在Omniglot中，字符被分组为字母表，tieredImageNet将类分组为更广泛的类别，对应于ImageNet（Deng等人，2009）层次结构中的更高级别节点。总共有34个类别，每个类别包含10到30个类别。这些被分为20个训练、6个验证和8个测试类别（数据集的详细信息可在补充材料中找到）。与miniImageNet和Vinyals等人（2016）提出的randImageNet等其他替代方案不同，这确保了所有训练类别与测试类别充分不同。例如，“管风琴”是一个训练类，“电吉他”是miniImagenet Ravi &Larochelle（2017）中的一个测试类，尽管它们都是乐器。这种情况不会发生在tieredImageNet中，因为“乐器”是一个高级类别，因此不分为培训类和测试类。这代表了一个更现实的小样本学习场景，因为一般来说，我们不能假设测试类别与训练中看到的类似。此外，tieredImageNet的分层结构对于可以利用类之间的层次关系的少量快照学习方法可能很有用。我们将这些有趣的扩展留给未来的工作。

5.2 Adapting the Datasets for Semi-supervised Learning

For each dataset, we first create an additional split to separate the images of each class into disjoint labeled and unlabeled sets. For Omniglot and tieredImageNet we sample 10% of the images of each class to form the labeled split. The remaining 90% can only be used in the unlabeled portion of episodes. For miniImageNet we use 40% of the data for the labeled split and the remaining 60% for the unlabeled, since we noticed that 10% was too small to achieve reasonable performance and avoid overfitting. We report the average classification scores over 10 random splits of labeled and unlabeled portions of the training set, with uncertainty computed in standard error (standard deviation divided by the square root of the total number of splits).

对于每个数据集，我们首先创建一个额外的分割，将每个类的图像分割为不相交的标记集和未标记集。对于Omniglot和tieredImageNet，我们对每个类的10%图像进行采样，以形成标记的分割。剩下的90%只能用于未标记的部分。对于miniImageNet，我们将40%的数据用于标记的拆分，剩余的60%用于未标记的拆分，因为我们注意到10%太小，无法实现合理的性能并避免过度拟合。我们报告了训练集有标签和无标签部分的10次随机分割的平均分类分数，不确定性以标准误差计算（标准偏差除以总分割数的平方根）。

We would like to emphasize that due to this labeled/unlabeled split, we are using strictly less label information than in the previously-published work on these datasets. Because of this, we do not expect our results to match the published numbers, which should instead be interpreted as an upperbound for the performance of the semi-supervised models defined in this work.

我们想强调的是，由于这种有标签/无标签的划分，我们使用的标签信息严格少于之前发表的关于这些数据集的工作。因此，我们不希望我们的结果与公布的数字相匹配，相反，这应该被解释为本研究中定义的半监督模型性能的上界。

Episode construction then is performed as follows. For a given dataset, we create a training episode by first sampling N classes uniformly at random from the set of training classes Ctrain. We then sample K images from the labeled split of each of these classes to form the support set, and M images from the unlabeled split of each of these classes to form the unlabeled set. Optionally, when including distractors, we additionally sample H other classes from the set of training classes and M images from the unlabeled split of each to act as the distractors. These distractor images are added to the unlabeled set along with the unlabeled images of the N classes of interest (for a total of MN + MH unlabeled images). The query portion of the episode is comprised of a fixed number of images from the labeled split of each of the N chosen classes. Test episodes are created analogously, but with the N classes (and optionally the H distractor classes) sampled from Ctest. In the experiments reported here we used H = N = 5, i.e. 5 classes for both the labeled classes and the distractor classes. We used M = 5 for training and M = 20 for testing in most cases, thus measuring the ability of the models to generalize to a larger unlabeled set size. Details of the dataset splits, including the specific classes assigned to train/validation/test sets, can be found in Appendices A and B.

然后按照以下步骤进行episode构建。对于给定的数据集，我们首先从训练类Ctrain集中均匀随机地抽样N个类来创建训练集。然后，我们从这些类中每个类的标记分割中抽取K个图像来形成支持集，从这些类中每个类的未标记分割中抽取M个图像来形成未标记集。或者，当包括干扰物时，我们从训练类集中另外抽取H个其他类，从每个班的未标记分割中抽取M个图像作为干扰物。这些干扰物图像与N类感兴趣的未标记图像一起添加到未标记集（对于总共MN+MH未标记图像）。插曲的查询部分由固定数量的图像组成，这些图像来自所选N个类中每个类的标记分割。测试片段是以类似的方式创建的，但是使用从Ctest中采样的N个类（以及可选的H个干扰物类）。在这里报告的实验中，我们使用了H=N=5，即标记类和干扰类各5个类。在大多数情况下，我们使用M=5进行训练，M=20进行测试，从而测量模型推广到更大的未标记集大小的能力。数据集分割的详细信息，包括分配给训练/验证/测试集的特定类别，可在附录A和B中找到。

In each dataset we compare our three semi-supervised models with two baselines. The first baseline, referred to as “Supervised” in our tables, is an ordinary Prototypical Network that is trained in a purely supervised way on the labeled split of each dataset. The second baseline, referred to as “Semi-Supervised Inference”, uses the embedding function learned by this supervised Prototypical Network, but performs semi-supervised refinement of the prototypes at test time using a step of Soft k-Means refinement. This is to be contrasted with our semi-supervised models that perform this refinement both at training time and at test time, therefore learning a different embedding function. We evaluate each model in two settings: one where all unlabeled examples belong to the classes of interest, and a more challenging one that includes distractors. Details of the model hyperparameters can be found in Appendix D and our online repository.在每个数据集中，我们比较三个半监督模型和两个基线。第一个基线在我们的表中被称为“监督的”，它是一个普通的原型网络，在每个数据集的标记分割上以纯粹监督的方式进行训练。第二个基线称为“半监督推理”，使用该监督原型网络学习的嵌入函数，但在测试时使用soft k-means细化步骤对原型进行半监督细化。这将与我们的半监督模型形成对比，我们的半监督模型在训练时和测试时都执行这种细化，因此学习不同的嵌入函数。我们在两种情况下评估每个模型：一种是所有未标记的示例都属于感兴趣的类别，另一种是更具挑战性的，包括干扰因素。模型超参数的详细信息可以在附录D和我们的在线存储库中找到。

5.3 RESULTS

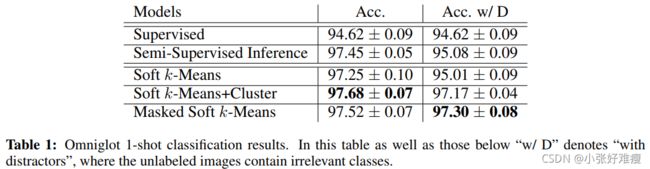
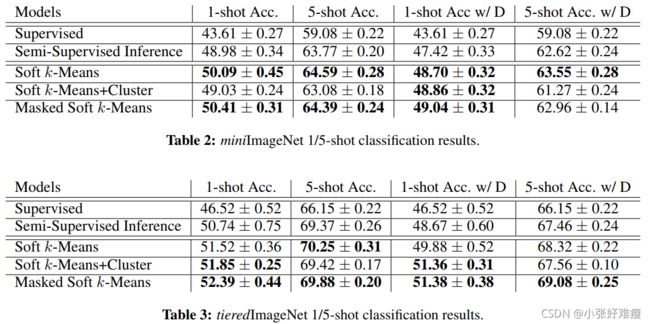
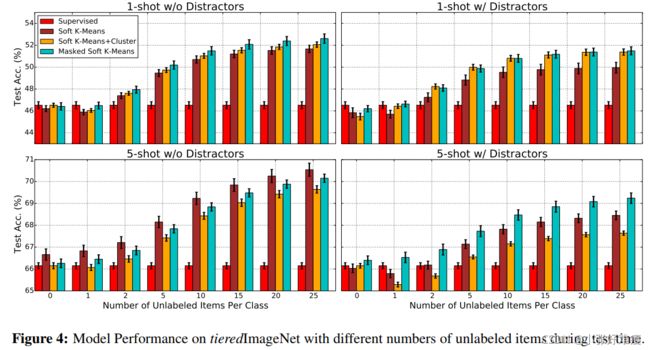
Results for Omniglot, miniImageNet and tieredImageNet are given in Tables 1, 2 and 5, respectively, while Figure 4 shows the performance of our models on tieredImageNet (our largest dataset) using different values for M (number of items in the unlabeled set per class). Additional results comparing the ProtoNet model to various baselines on these datasets, and analysis of the performance of the Masked Soft k-Means model can be found in Appendix C.

Omniglot、miniImageNet和tieredImageNet的结果分别在表1、2和5中给出，而图4显示了我们的模型在tieredImageNet（我们最大的数据集）上的性能，使用不同的M值（每个类中未标记集的项数）。附录C中提供了将ProtoNet模型与这些数据集上的各种基线进行比较的其他结果，以及对屏蔽软k-均值模型性能的分析。

 

 Across all three benchmarks, at least one of our proposed models outperforms the baselines,
demonstrating the effectiveness of our semi-supervised meta-learning procedure. In the nondistractor settings, all three proposed models outperform the baselines in almost all the experiments, without a clear winner between the three models across the datasets and shot numbers. In the scenario where training and testing includes distractors, Masked Soft k-Means shows the most robust performance across all three datasets, attaining the best results in each case but one. In fact this model reaches performance that is close to the upper bound based on the results without distractors.

在所有三个基准中，我们提出的模型中至少有一个优于基线，证明了我们的半监督元学习过程的有效性。在非Distractor设置下，几乎所有实验中，所有三个提出的模型都优于基线，在数据集和放炮数量上，三个模型之间没有明显的赢家。在训练和测试包括干扰因素的场景中，Masked Soft k-Means在所有三个数据集中显示出最稳健的性能，在除一个之外的每种情况下都能获得最佳结果。事实上，在没有干扰因素的情况下，该模型达到了接近上限的性能。

From Figure 4, we observe clear improvements in test accuracy when the number of items in the
unlabeled set per class grows from 0 to 25. These models were trained with M = 5 and thus are
showing an ability to extrapolate in generalization. This confirms that, through meta-training, the
models learn to acquire a better representation that is improved by semi-supervised refinement.

从图4中，我们观察到，当每个类的未标记集合中的项目数从0增加到25时，测试精度明显提高。这些模型是用M=5训练的，因此显示出在推广中进行外推的能力。这证实了，通过元训练，模型学习获得更好的表示，并通过半监督细化进行改进。

6 Conclusion

In this work, we propose a novel semi-supervised few-shot learning paradigm, where an unlabeled set is added to each episode. We also extend the setup to more realistic situations where the unlabeled set has novel classes distinct from the labeled classes. To address the problem that current fewshot classification datasets are too small for a labeled vs. unlabeled split and also lack hierarchical levels of labels, we introduce a new dataset, tieredImageNet. We propose several novel extensions of Prototypical Networks, and they show consistent improvements under semi-supervised settings compared to our baselines. As future work, we are working on incorporating fast weights (Ba et al., 2016; Finn et al., 2017) into our framework so that examples can have different embedding representations given the contents in the episode.

在这项工作中，我们提出了一种新的半监督小样本学习范式，其中一个未标记集被添加到每一集。我们还将设置扩展到更现实的情况，其中未标记集具有不同于标记类的新类。为了解决当前小样本分类数据集太小，无法进行标记与未标记的分割，并且缺少分层的标签的问题，我们引入了一个新的数据集tieredImageNet。我们提出了几种新的原型网络扩展，与我们的基线相比，它们在半监督设置下表现出一致的改进。作为未来的工作，我们正在努力将快速权重（Ba等人，2016；Finn等人，2017）纳入我们的框架中，以便示例可以具有不同的嵌入表示形式，给定该episode中的内容。