吴恩达ML WEEK3 练习一代码（线性回归）

---

0 总结

学习时间：2022.9.12~2022.9.18

• 复习单变量线性回归和多变量线性回归
• 复习MATLAB软件的使用
• 利用所学知识，完成单变量线性回归代价函数计算、梯度下降的代码编写
• 利用所学知识，完成多变量线性回归代价函数计算、梯度下降的代码编写，以及正规方程法求解$\theta$的代码编写。
• 熟悉了使用梯度下降法求解线性回归的流程和代码，可以很好地运用MATLAB求解问题

---

1 简单MATLAB函数

---

1.2 warmUpExercise.m

用途：返回5*5的单位阵。
代码：

function A = warmUpExercise()
	A = eye(5);
end

---

2 单变量线性回归

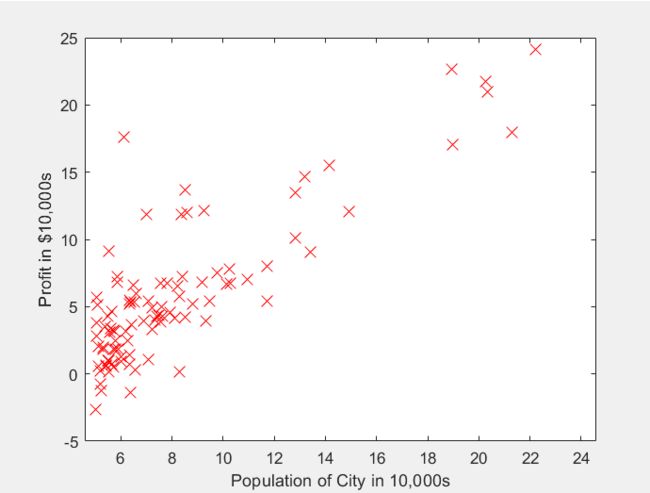
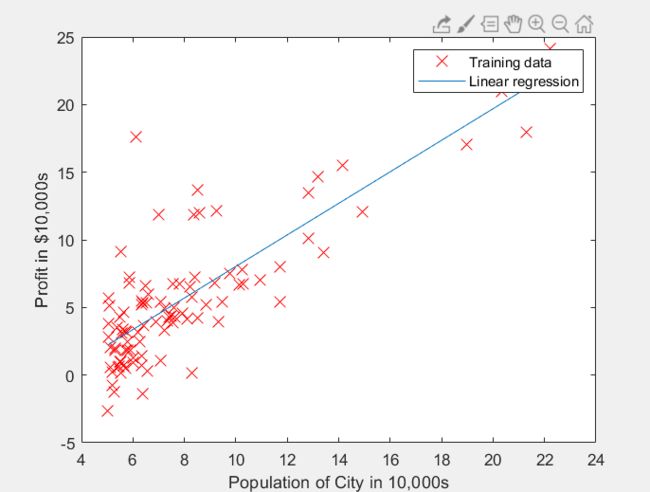
问题描述：ex1data1.txt包含所有数据集，第一列是城市的人口，第二列是该城市的收益（负数表示亏本）。你需要使用这个数据预测下一个扩张的城市。

---

2.1 绘制

任务：补充plotData.m，绘制数据。
代码：

function plotData(x, y)
	figure; % open a new figure window
	plot(x,y,'rx','MarkerSize',10);
	ylabel('Profit in $10,000s');
	xlabel('Population of City in 10,000s');
end

运行结果：

---

2.2 梯度下降

任务：计算线性回归参数$\theta$。

2.2.1 更新公式

假设函数是关于$x$的函数：$$h_{\theta }(x)={\theta }^{T}x={\theta }_0+{\theta }_{1}x$$代价函数是关于${\theta }_0,{\theta }_1$的函数：
$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i{)}^2$$优化目标是寻求使得代价函数最小的${\theta }_0,{\theta }_1$:$$\underset{{\theta }_0,{\theta }_1}{\min }J(\theta )$$其中一个方法是使用梯度下降，每次迭代过程中的更新公式：

2.2.2 实施

在此前，我们已经导入了数据，x和y都是m列的数据，其中x中每一行表示每一个样本，为了与$\theta$相匹配，我们需要给x每一行增加一个$x_0$=1。初始化迭代次数为1500，学习率为0.01。
代码：

X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters

% Some gradient descent settings
iterations = 1500;
alpha = 0.01;

2.2.3 完成代价函数的计算

任务：完成computeCost.m
代码：

function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
%   J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
%   parameter for linear regression to fit the data points in X and y

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
%               You should set J to the cost.
h = X*theta; % m*1的矩阵，每一行对应每个样本的预测值h
J = 1/(2*m)*sum((h-y).^2);
% =========================================================================

end

运行结果：

2.2.4 梯度下降

任务：完成gradientDescent.m
代码：

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
%   theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by 
%   taking num_iters gradient steps with learning rate alpha

% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1); % 记录每次迭代得到的J，如果正确的话是按迭代次数递减的

for iter = 1:num_iters

    % ====================== YOUR CODE HERE ======================
    % Instructions: Perform a single gradient step on the parameter vector
    %               theta. 
    %
    % Hint: While debugging, it can be useful to print out the values
    %       of the cost function (computeCost) and gradient here.
    %
    h = X*theta; % m*1的矩阵，每一行对应每个样本的预测值h
    theta = theta - alpha / m * (X' * (h - y));
    % ============================================================

    % Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);

end

end

结果：

---

3 多变量线性回归

问题描述：ex1data2.txt包含了关于房价的所有数据集，第一列是房子大小，第二列是卧室数量，第三列是房子价格。

---

3.1 特征归一化

$$x_n^{(i)}=\frac{x_n^{(i)}-u_n}{s_n}$$其中，$u_n$是平均值，$s_n$是标准差，也可以用最大值-最小值代替。这样算得的x会在-0.5到0.5之间。
任务：完成featureNormalize.m中的代码，首先计算平均值存在mu数组，然后除以标准差（standard deviation）
代码：

function [X_norm, mu, sigma] = featureNormalize(X)
%FEATURENORMALIZE Normalizes the features in X 
%   FEATURENORMALIZE(X) returns a normalized version of X where
%   the mean value of each feature is 0 and the standard deviation
%   is 1. This is often a good preprocessing step to do when
%   working with learning algorithms.

% You need to set these values correctly
X_norm = X;
mu = zeros(1, size(X, 2)); % size(X, 2)特征数
sigma = zeros(1, size(X, 2));

% ====================== YOUR CODE HERE ======================
% Instructions: First, for each feature dimension, compute the mean
%               of the feature and subtract it from the dataset,
%               storing the mean value in mu. Next, compute the 
%               standard deviation of each feature and divide
%               each feature by it's standard deviation, storing
%               the standard deviation in sigma. 
%
%               Note that X is a matrix where each column is a 
%               feature and each row is an example. You need 
%               to perform the normalization separately for 
%               each feature. 
%
% Hint: You might find the 'mean' and 'std' functions useful.
% 平均值储存在mu，标准差储存在sigma
mu = mean(X,1); % 计算每一列的均值，1表示列
sigma = std(X,1); 5 计算每一行的标准差，1表示列
% X = (X-mu)./sigma;
for i=1:size(X,2)
    % 对每一列X做如下操作
    % 易错点：起初把i写成了1
    X_norm(:,i) = (X(:,i)-mu(i))./sigma(i);
end
% ============================================================

end

---

3.2 梯度下降

任务：完成多特征回归的梯度下降，完成computeCostMulti.m 和gradientDescentMulti.m的代码。
提示：可以用size(X,2)看有多少特征。

computeCostMulti.m代码（和单变量一样）：

function J = computeCostMulti(X, y, theta)
%COMPUTECOSTMULTI Compute cost for linear regression with multiple variables
%   J = COMPUTECOSTMULTI(X, y, theta) computes the cost of using theta as the
%   parameter for linear regression to fit the data points in X and y

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
%               You should set J to the cost.
h = X * theta;
J = 1/(2*m)*sum((h-y).^2);
% =========================================================================

end

gradientDescentMulti.m代码（和单变量一样）：

function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
%GRADIENTDESCENTMULTI Performs gradient descent to learn theta
%   theta = GRADIENTDESCENTMULTI(x, y, theta, alpha, num_iters) updates theta by
%   taking num_iters gradient steps with learning rate alpha

% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);

for iter = 1:num_iters

    % ====================== YOUR CODE HERE ======================
    % Instructions: Perform a single gradient step on the parameter vector
    %               theta. 
    %
    % Hint: While debugging, it can be useful to print out the values
    %       of the cost function (computeCostMulti) and gradient here.
    %
    h = X * theta;
    theta = theta - alpha / m * (X' * (h - y));
    % ============================================================

    % Save the cost J in every iteration    
    J_history(iter) = computeCostMulti(X, y, theta);

end

end

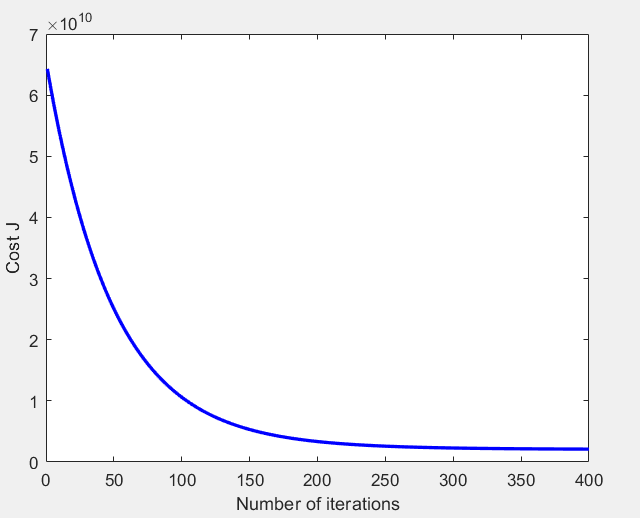
运行结果：
①随着每次迭代代价函数的变化：

②得到的$\theta$值：

3.2.1 预测

预测面积为1650，卧室个数为3的房子价格
预测结果是$289221.547371

% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
% Recall that the first column of X is all-ones. Thus, it does
% not need to be normalized.
X_test = [1650 3];
X_test = [1 (X_test-mu)./sigma];
y_predict = X_test*theta;

---

3.3 正规方程

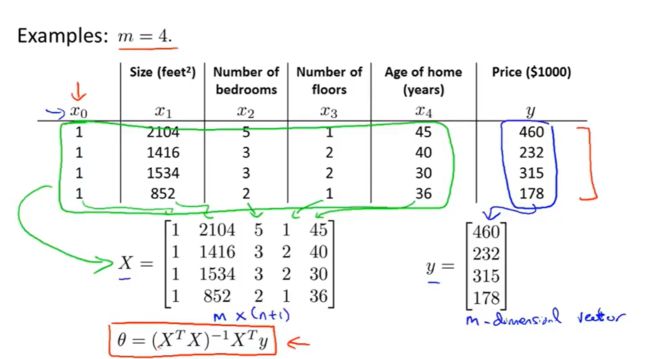
任务：完成normalEqn.m，实现正规方程对$\theta$的求解。
只需在normalEqn.m中加入一行代码：

theta = pinv(X'*X)*X'*y;

运行结果：
—