吴恩达ML WEEK4 逻辑回归+正则化
吴恩达机器学习 第四周
- 0 总结
- 1 逻辑回归(Logistic Regression)
-
- 1.1 分类问题
- 1.2 假说 h θ ( x ) h_\theta(x) hθ(x)的表示
- 1.3 决策边界(decision boundary)
- 1.4 代价函数
- 1.5 梯度下降
- 1.6 高级优化
- 1.7 一对多分类算法
- 2 正则化
-
- 2.1 过拟合问题
- 2.2 代价函数
- 2.3 线性回归的正则化
- 2.4 逻辑回归的正则化
0 总结
学习时间:2022.9.26~2022.10.2
- 学习逻辑回归
- 学习正则化
- 学习线性回归和逻辑回归的正则化
1 逻辑回归(Logistic Regression)
1.1 分类问题
线性回归的缺点探讨
对于肿瘤分类问题,假设只有一个特征值——肿瘤大小,已知,肿瘤越大,为恶性肿瘤的可能性越大。

图中,位于0的为良性肿瘤,位于1的为恶性肿瘤,我们可以通过线性回归构造洋
红色的直线来进行分类,规定 h θ ( x ) ≥ 0.5 h_\theta(x)\geq0.5 hθ(x)≥0.5则预测为恶性肿瘤( y = 1 y=1 y=1),否则为良性肿瘤( y = 0 y=0 y=0)。
所以可以得出结论:在洋红色竖线左侧的点都会被预测为良性肿瘤,右侧都会被预测为恶性肿瘤。
那么,线性回归得到的假设函数如图
蓝色线条所示,在蓝色竖线左侧的点都会被预测为良性肿瘤,右侧都会被预测为恶性肿瘤。但是实际上应该以红色竖线为标准。
此外:
线性回归: 预测值要求是0或者1,但是 h θ ( x ) h_\theta(x) hθ(x)会大于1或者小于0。
逻辑回归: 0 ≤ h θ ( x ) ≤ 1 0\leq h_\theta(x)\leq1 0≤hθ(x)≤1
逻辑回归的假设函数可以理解成,线性回归的假设函数基础上套上sigmoid函数
!实际上逻辑回归是分类问题。
1.2 假说 h θ ( x ) h_\theta(x) hθ(x)的表示
sigmoid function(also:logistic function)
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1

可以看出,
sigmoid函数取值在(0,1)之间,是递增函数。
h θ ( x ) h_\theta(x) hθ(x)
对于logistic regression model,要求 0 ≤ h θ ( x ) ≤ 1 0\leq h_\theta(x)\leq1 0≤hθ(x)≤1,那么可以令 h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^Tx) hθ(x)=g(θTx),其中, g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1,这样, h θ ( x ) h_\theta(x) hθ(x)一定在0到1之间。
因此, h θ ( x ) h_\theta(x) hθ(x)表达式`:
h θ ( x ) = 1 1 + e − θ T x h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}} hθ(x)=1+e−θTx1
h θ ( x ) h_\theta(x) hθ(x)的解释

以肿瘤为例,如果输入 x x x,得到 h θ ( x ) = 0.7 h_\theta(x)=0.7 hθ(x)=0.7,那么表示这个病人有70%的概率是恶性肿瘤。
因此, h θ ( x ) h_\theta(x) hθ(x)表示在给定 x x x以及参数 θ \theta θ的情况下, y = 1 y=1 y=1的概率,即: h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_\theta(x)=P(y=1|x;\theta) hθ(x)=P(y=1∣x;θ)那么 y = 0 y=0 y=0的概率: P ( y = 0 ∣ x ; θ ) = 1 − P ( y = 1 ∣ x ; θ ) P(y=0|x;\theta)=1-P(y=1|x;\theta) P(y=0∣x;θ)=1−P(y=1∣x;θ)
1.3 决策边界(decision boundary)
线性决策边界
此前,我们假设 h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^Tx) hθ(x)=g(θTx),其中, g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1。
在逻辑回归中,我们预测,当 h θ ( x ) h_\theta(x) hθ(x)大于等于0.5时,y=1;当 h θ ( x ) h_\theta(x) hθ(x)小于0.5时,y=0。根据绘制的sigmoid函数图像,我们知道:
当 θ T x = 0 \theta^Tx=0 θTx=0时, h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^Tx) hθ(x)=g(θTx)=0.5, y y y=1;
当 θ T x > 0 \theta^Tx>0 θTx>0时, h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^Tx) hθ(x)=g(θTx)>0.5, y y y=1;
当 θ T x < 0 \theta^Tx<0 θTx<0时, h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^Tx) hθ(x)=g(θTx)<0.5, y y y=0。

举一个具体的例子:

在这里,利用下一节的算法,得到 h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 ) = g ( − 3 + x 1 + x 2 ) h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2)=g(-3+x_1+x_2) hθ(x)=g(θ0+θ1x1+θ2x2)=g(−3+x1+x2),那么当 θ T x ≥ 0 \theta^Tx\geq0 θTx≥0时,也就是 − 3 + x 1 + x 2 ≥ 0 -3+x_1+x_2\geq0 −3+x1+x2≥0时,模型预测 y = 1 y=1 y=1。
那么 x 1 + x 2 = 3 x_1+x_2=3 x1+x2=3这条直线(图中洋红色)就是决策边界,其左下方圆圈为y=0,右上方为y=1。
非线性决策边界
假使我们的数据呈现这样的分布情况,怎样的模型才能适合呢?

假设 h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 2 2 ) = g ( − 1 + x 1 2 + x 2 2 ) h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_2^2)=g(-1+x_1^2+x_2^2) hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x22)=g(−1+x12+x22),那么当 − 1 + x 1 2 + x 2 2 ≥ 0 -1+x_1^2+x_2^2\geq0 −1+x12+x22≥0时,模型预测 y = 1 y=1 y=1。也就是说,
判定边界是一个圆形。
总结
① 逻辑回归是一个分类问题(?二分类),它的结果不是0就是1。判断0或者1,是根据g括号内的内容决定的,如果g括号中大于等于0,则判断为1。
② 一旦参数 θ \theta θ确定,那么决策边界也就确定了。
③ 决策边界的形状:令g(?)中的?=0就是。如果?中有1个参数,决策边界是点;如果有两个参数,决策边界是边…
1.4 代价函数
变量说明
| 变量 | 含义 |
|---|---|
| m m m | 训练集中实例的数量 |
| n n n | 有n个特征 |
| x x x | 特征/输入变量(这个例子中是房子的大小) |
| y y y | 目标变量/输出变量(这个例子中是房子的价格) |
| ( x , y ) (x,y) (x,y) | 训练集中的实例 |
| ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)} ) (x(i),y(i)) | 第 i 个观察实例 |
| h h h | 学习算法的解决方案或函数也称为假设(hypothesis) |
假设训练集一共有m个样本:
{ ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . , ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})\} {(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}每一个输入 x x x都是n+1维向量:
x ∈ [ x 0 x 1 . . . x n ] ,其中 x 0 = 1 x\in\begin{bmatrix}x_0 \\x_1\\...\\x_n \end{bmatrix},其中x_0=1 x∈⎣ ⎡x0x1...xn⎦ ⎤,其中x0=1每一个输出都满足 y ∈ { 0 , 1 } y\in\{0,1\} y∈{0,1},也就是说 y = 1 或者 y = 0 y=1或者y=0 y=1或者y=0。
假设函数表达式:
h θ ( x ) = 1 1 + e − θ T x h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}} hθ(x)=1+e−θTx1
回顾
在线性回归中,定义过代价函数: J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x i ) − y i ) 2 J(\theta_0,\theta_1)=\frac{1}{2m}\sum^{m}_{i=1}(h_\theta(x^{i})-y^{i})^{2} J(θ0,θ1)=2m1i=1∑m(hθ(xi)−yi)2定义一个cost项:
C o s t ( h θ ( x i ) , y ( i ) ) = 1 2 ( h θ ( x i ) − y ( i ) ) 2 Cost(h_\theta(x^{i}),y^{(i)})=\frac{1}{2}(h_\theta(x^{i})-y^{(i)})^2 Cost(hθ(xi),y(i))=21(hθ(xi)−y(i))2但是如果我们在逻辑回归中运用这种cost项,那么得到的代价函数是非凸函数(non-convex function),如左图所示,有很多局部最优值。
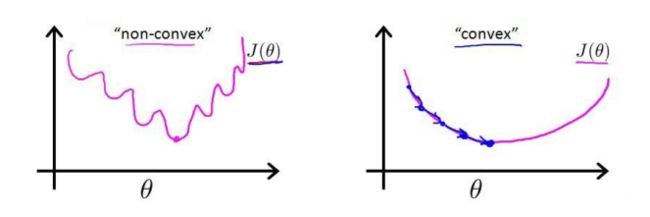
逻辑回归的代价函数
代价函数表达式:
J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)}) J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))其中:
C o s t ( h θ ( x ) , y ) = { − l o g ( h θ ( x ) ) i f y = 1 − l o g ( 1 − h θ ( x ) ) i f y = 0 Cost(h_\theta(x),y)= \begin{cases} -log(h_\theta(x))&if\ y=1\\ -log(1-h_\theta(x))&if\ y=0 \end{cases} Cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x))if y=1if y=0
这样定义的代价函数是一个凸函数并且可以求出它的最优值。
对Cost的理解
首先,明确 h θ ( x ) h_\theta(x) hθ(x)是0到1之间的(因为是sigmoid函数得到的)。
y=1的情况:

注意到横坐标是 h θ ( x ) h_\theta(x) hθ(x),表示 h θ ( x ) h_\theta(x) hθ(x)越接近于1,那么代价越小; h θ ( x ) h_\theta(x) hθ(x)越接近于0,那么代价越接近于无穷。
1.5 梯度下降
根据上一节的内容,简写代价函数:
J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)}) J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))其中:
C o s t ( h θ ( x ) , y ) = − y l o g ( h θ ( x ) ) − ( 1 − y ) l o g ( 1 − h θ ( x ) ) Cost(h_\theta(x),y)=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x)) Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))注意: y = 0 y=0 y=0或者 y = 1 y=1 y=1。
所以,代价函数:
J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) = − 1 m [ ∑ i = 1 m y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] \begin{align} J(\theta) & = \frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)}) \notag\\ & = -\frac{1}{m}[\sum_{i=1}^m y^{(i)} log(h_\theta(x^{(i)}))+(1-y^{(i)} )log(1-h_\theta(x^{(i)} ))]\notag \end{align} J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))=−m1[i=1∑my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
当前要做的是:寻找合适的参数 θ \theta θ使得 J ( θ ) J(\theta) J(θ)最小;找到 θ \theta θ后,在给定某个输入 x x x可以预测出 h θ ( x ) h_\theta(x) hθ(x)。
作法:
Repeat{
θ j : = θ j − α ∂ J ( θ ) ∂ θ j : = θ j − α ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \begin{align} \theta_j& :=\theta_j-\alpha\frac{\partial J(\theta)}{\partial \theta_j} \notag\\ & :=\theta_j-\alpha\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}\notag \end{align} θj:=θj−α∂θj∂J(θ):=θj−αi=1∑m(hθ(x(i))−y(i))xj(i)}
1.6 高级优化
举例
现有一个含两个参数的问题,这两个参数为: θ = [ θ 1 θ 2 ] \theta= \begin{bmatrix} \theta_1\\\theta_2 \end{bmatrix} θ=[θ1θ2],代价函数 J ( θ ) = ( θ 1 − 5 ) 2 + ( θ 2 − 5 ) 2 J(\theta)=(\theta_1-5)^2+(\theta_2-5)^2 J(θ)=(θ1−5)2+(θ2−5)2,那么梯度: ∂ J ( θ ) ∂ θ 1 = 2 ( θ 1 − 5 ) , ∂ J ( θ ) ∂ θ 2 = 2 ( θ 2 − 5 ) \frac{\partial J(\theta)} {\partial \theta_1}=2(\theta_1-5),\frac{\partial J(\theta)} {\partial \theta_2}=2(\theta_2-5) ∂θ1∂J(θ)=2(θ1−5),∂θ2∂J(θ)=2(θ2−5)。很明显,当 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2都等于5的时候,代价最小为0。
如果我们不知道最小值,需要使用代价函数找到最小值,那么首先需要编写一个costFunction函数,输入 θ \theta θ,获得对应的代价 j V a l jVal jVal和梯度 g r a d i e n t gradient gradient:
function [jVal, gradient]=costFunction(theta)
jVal=(theta(1)-5)^2+(theta(2)-5)^2;
gradient=zeros(2,1);
gradient(1)=2*(theta(1)-5);
gradient(2)=2*(theta(2)-5);
end
利用fminunc函数(无约束最小化函数)求解:
%% 'GradObj','on'表示设置梯度目标参数为打开,意味着现在要给这个算法提供一个梯度;
%% 'MaxIter',100设置最大迭代次数为100
options=optimset('GradObj','on','MaxIter',100);
initialTheta=zeros(2,1); %% 初始化theta为0
%% optTheta:最终的theta值
%% functionVal:最后一次迭代的代价函数值,为0表示收敛
%% exitFlag:=1表示收敛
[optTheta, functionVal, exitFlag]=fminunc(@costFunction, initialTheta, options); %% optTheta:最终的theta值
1.7 一对多分类算法
首先有三种类别:第一类:三角形,第二类:正方形,第三类:叉。
将属于第一类的记为1,其余记为0,可以得到假设函数 h θ ( 1 ) ( x ) h_\theta^{(1)}(x) hθ(1)(x),表示第一类的假设函数,即属于第一类的可能性是多少。
将属于第二类的记为1,其余记为0,可以得到假设函数 h θ ( 2 ) ( x ) h_\theta^{(2)}(x) hθ(2)(x),表示第二类的假设函数,即属于第二类的可能性是多少。
…
注意:不同假设函数, θ \theta θ取值是不同的。
总结:多分类问题求解步骤
①对于每一个类 i i i,训练一个逻辑回归分类器 h θ ( i ) ( x ) h_\theta^{(i)}(x) hθ(i)(x),来预测 y = i y=i y=i的概率。
②对于一个新的输入 x x x,选择满足: max i h θ ( i ) ( x ) \max \limits_{i}h_\theta^{(i)}(x) imaxhθ(i)(x)的 i i i作为其类别。
2 正则化
2.1 过拟合问题
欠拟合、刚好拟合、过拟合
过拟合
往往在特征过多的时候出现。我们通过学习得到的假设可能能够非常好地适应训练集(代价函数可能几乎为 0),但是可能会不能推广到新的数据。
解决过拟合
一种方法是绘制出假设函数,看是否很扭曲,从而判断多项式阶次。
但是,当有很多特征,很少训练集的时候,也会出现过拟合问题。
1、减少特征数量
——人为选出需要的特征。
——模型选择算法(自动选择保留的特征)
2、正则化
——保留所有的特征,但是减少参数 θ j \theta_j θj的量级/值。
2.2 代价函数
要使右边的过拟合变成左边的正确的拟合,那么需要使 θ 3 x 3 \theta_3x^3 θ3x3和 θ 4 x 4 \theta_4x^4 θ4x4这两项为0。
那么,改写代价函数使得 θ 3 θ 4 \theta3\ \theta4 θ3 θ4非常小,也就是在原先代价函数基础上加上 1000 θ 3 2 + 1000 θ 4 2 1000\theta_3^2+1000\theta_4^2 1000θ32+1000θ42。
正则化
减小参数 θ 0 , θ 1 , . . . . . . , θ n \theta_0,\theta_1,......,\theta_n θ0,θ1,......,θn的值
——简化假设函数
——减少过拟合,使假设函数更加平滑
另一个例子
预测房价问题:
——100个特征: x 1 , x 2 , . . . . . . , x 100 x_1,x_2,......,x_{100} x1,x2,......,x100
——101个参数: θ 0 , θ 1 , . . . . . . , θ 100 \theta_0,\theta_1,......,\theta_{100} θ0,θ1,......,θ100
此时,我们不知道应该选择哪个参数来减小它的值,所以,缩小所有的参数(惩罚项):
J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) − y ( i ) ) 2 + λ ∑ i = 1 m θ j 2 ] J(\theta)=\frac{1}{2m} [ \sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)})^2+\lambda \sum^m_{i=1}\theta_j^2 ] J(θ)=2m1[i=1∑m(hθ(x(i)−y(i))2+λi=1∑mθj2] 注意,我们没有给 θ 0 \theta_0 θ0增加惩罚项!
λ \lambda λ越大,对参数的惩罚就越大,最后所有的参数都会接近于0,只剩下 θ 0 \theta_0 θ0,造成欠拟合。
2.3 线性回归的正则化
1 − α 1 m 1-\alpha \frac{1}{m} 1−αm1是一个很接近1的数,比如0.99。











