浅谈非线性回归(non-linear regression)
文章目录
- 浅谈非线性回归(non-linear regression)
-
- 引言
- 最小二乘多项式拟合
- 非线性拟合
-
- G a u s s – N e w t o n Gauss–Newton Gauss–Newton算法[1]
- L e v e n b e r g – M a r q u a r d t Levenberg–Marquardt Levenberg–Marquardt算法[2]
- Q u a s i − N e w t o n Quasi-Newton Quasi−Newton方法(准 N e w t o n Newton Newton法/拟 N e w t o n Newton Newton法)[3]
- N e l d e r – M e a d Nelder–Mead Nelder–Mead方法[7]\[8]
- 模拟退火(simulated annealing)[10]
- 总结
- 参考文献
浅谈非线性回归(non-linear regression)
引言
这是学习了最小二乘拟合并编程后的一次大作业
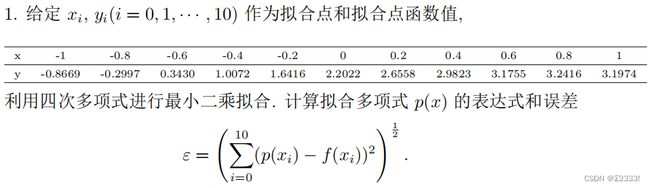
题目:
完整代码可参见本人GitHub仓库
最小二乘多项式拟合
回顾最小二乘多项式拟合,最小二乘多项式拟合是利用最小二乘法寻找一个多项式 P ∗ ∈ P n P^*\in \mathcal{P_n} P∗∈Pn,使其能够拟合离散数据 ( x k , f ( x k ) ) , k = 0 , 1 , ⋯ , m (x_k,f(x_k)),k=0,1,\cdots,m (xk,f(xk)),k=0,1,⋯,m
∣ ∣ f − P ∗ ∣ ∣ 2 2 = min P ∈ P n ∣ ∣ f − P ∣ ∣ 2 2 = min P ∈ P n ∑ k = 0 m [ f ( x k ) − P ( x k ) ] 2 ||f-P^*||^2_2=\min_{P\in\mathcal{P_n}}||f-P||^2_2=\min_{P\in\mathcal{P_n}}\sum_{k=0}^m[f(x_k)-P(x_k)]^2 ∣∣f−P∗∣∣22=P∈Pnmin∣∣f−P∣∣22=P∈Pnmink=0∑m[f(xk)−P(xk)]2
设 P n = S p a n { φ 0 , φ 1 , ⋯ , φ n } \mathcal{P}_n=Span\{\varphi_0,\varphi_1,\cdots,\varphi_n\} Pn=Span{φ0,φ1,⋯,φn},其中 { φ i } \{\varphi_i\} {φi}线性无关,则任意多项式 P ∗ ∈ P n P^*\in \mathcal{P_n} P∗∈Pn可以写成
P ( x ) = a 0 φ 0 ( x ) + a 1 φ 1 ( x ) + ⋯ + a n φ n ( x ) = ∑ i = 0 n a i φ i ( x ) P(x)=a_0\varphi_0(x)+a_1\varphi_1(x)+\cdots+a_n\varphi_n(x)=\sum_{i=0}^na_i\varphi_i(x) P(x)=a0φ0(x)+a1φ1(x)+⋯+anφn(x)=i=0∑naiφi(x)
此时多项式拟合问题转化为一个具有 n + 1 n+1 n+1个变量的多元函数最小值问题
E ( a 0 , a 1 , ⋯ , a n ) = ∣ ∣ f − P ∣ ∣ 2 2 = ∑ k = 0 m [ f ( x k ) − ∑ i = 0 n a i φ i ( x k ) ] 2 E(a_0,a_1,\cdots,a_n)=||f-P||^2_2=\sum_{k=0}^m\left[f(x_k)-\sum_{i=0}^na_i\varphi_i(x_k)\right]^2 E(a0,a1,⋯,an)=∣∣f−P∣∣22=k=0∑m[f(xk)−i=0∑naiφi(xk)]2
为了使 E E E最小,需要使
∂ E ∂ a i = 0 , i = 0 , 1 , ⋯ , n \dfrac{\partial E}{\partial a_i}=0,i=0,1,\cdots,n ∂ai∂E=0,i=0,1,⋯,n
即
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ 0=\dfrac{\part…
因此,得到线性方程组
∑ j = 0 n a j ⟨ φ i , φ j ⟩ = ⟨ φ i , f ⟩ , i = 0 , 1 , ⋯ , n \sum_{j=0}^n a_j\langle \varphi_i,\varphi_j\rangle=\langle \varphi_i,f\rangle,i=0,1,\cdots,n j=0∑naj⟨φi,φj⟩=⟨φi,f⟩,i=0,1,⋯,n
将其写成矩阵形式 G a = d Ga=d Ga=d,其中
G = ( ⟨ φ 0 , φ 0 ⟩ ⟨ φ 0 , φ 1 ⟩ ⋯ ⟨ φ 0 , φ n ⟩ ⟨ φ 1 , φ 0 ⟩ ⟨ φ 1 , φ 1 ⟩ ⋯ ⟨ φ 1 , φ n ⟩ ⋮ ⋮ ⋱ ⋮ ⟨ φ n , φ 0 ⟩ ⟨ φ n , φ 1 ⟩ ⋯ ⟨ φ n , φ n ⟩ ) , a = ( a 0 a 1 ⋮ a n ) , d = ( ⟨ φ 0 , f ⟩ ⟨ φ 1 , f ⟩ ⋮ ⟨ φ n , f ⟩ ) G = \begin{pmatrix} \langle \varphi_0,\varphi_0\rangle &\langle \varphi_0,\varphi_1\rangle&\cdots &\langle \varphi_0,\varphi_n\rangle\\ \langle \varphi_1,\varphi_0\rangle &\langle \varphi_1,\varphi_1\rangle&\cdots &\langle \varphi_1,\varphi_n\rangle\\ \vdots&\vdots&\ddots&\vdots\\ \langle \varphi_n,\varphi_0\rangle &\langle \varphi_n,\varphi_1\rangle&\cdots &\langle \varphi_n,\varphi_n\rangle \end{pmatrix}, a = \begin{pmatrix} a_0\\ a_1\\ \vdots\\ a_n \end{pmatrix}, d = \begin{pmatrix} \langle \varphi_0,f\rangle\\ \langle \varphi_1,f\rangle\\ \vdots\\ \langle \varphi_n,f\rangle \end{pmatrix} G=⎝⎜⎜⎜⎛⟨φ0,φ0⟩⟨φ1,φ0⟩⋮⟨φn,φ0⟩⟨φ0,φ1⟩⟨φ1,φ1⟩⋮⟨φn,φ1⟩⋯⋯⋱⋯⟨φ0,φn⟩⟨φ1,φn⟩⋮⟨φn,φn⟩⎠⎟⎟⎟⎞,a=⎝⎜⎜⎜⎛a0a1⋮an⎠⎟⎟⎟⎞,d=⎝⎜⎜⎜⎛⟨φ0,f⟩⟨φ1,f⟩⋮⟨φn,f⟩⎠⎟⎟⎟⎞
G G G被称为 G r a m Gram Gram矩阵,若 G G G非奇异,则方程有唯一解 a ∗ = { a 0 ∗ , a 1 ∗ , ⋯ , a n ∗ } T a^*=\{a_0^*,a_1^*,\cdots,a_n^*\}^T a∗={a0∗,a1∗,⋯,an∗}T,最小二乘拟合多项式为
P ∗ ( x ) = a 0 ∗ φ 0 ( x ) + a 1 ∗ φ 1 ( x ) + ⋯ + a n ∗ φ n ( x ) P^*(x)=a^*_0\varphi_0(x)+a^*_1\varphi_1(x)+\cdots+a^*_n\varphi_n(x) P∗(x)=a0∗φ0(x)+a1∗φ1(x)+⋯+an∗φn(x)
对于第一题,代码如下
#include 结果为:
非线性拟合
求解非线性最小二乘问题的算法一般有两类,分别是线搜索法(line search methods)和信任域法(trust region methods),而在实际应用中,二者往往结合起来使用。以下将介绍四种基本的非线性拟合方法,另外,随着机器学习的发展,逐渐出现了将模拟退火、遗传算法等结合非线性拟合的算法,对于传统非线性拟合算法收敛于局部最优解的情况进行改进。
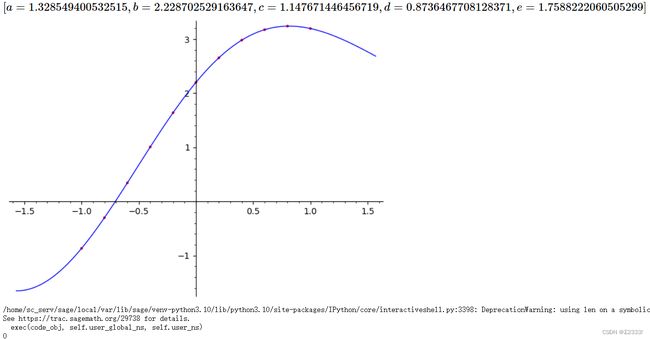
对于第二题,我们要拟合的目标函数为 p ( x ) = a 0 + a 1 s i n ( a 2 x ) + a 3 c o s ( a 4 x ) p(x)=a_0+a_1sin(a_2x)+a_3cos(a_4x) p(x)=a0+a1sin(a2x)+a3cos(a4x),先使用 S a g e M a t h SageMath SageMath进行曲线拟合,代码如下:
# for this example, we first generate some data with built-in variance:
x = [-1, -0.8, -0.6, -0.4, -0.2, 0.0, 0.2, 0.4, 0.6, 0.8, 1.0]
y = [-0.8669, -0.2997, 0.3430, 1.0072, 1.6416, 2.2022, 2.6558, 2.9823, 3.1755, 3.2416, 3.1974]
data = [(x[i], y[i]) for i in range(len(x))]
# design a model with adjustable parameters a,b,c that describes the data
var('a, b, c, d, e, x')
model(x) = a + b * sin(c * x) + d * cos(e * x)
# calculate the values of the parameters that best fit the model to the data
sol = find_fit(data,model)
show(sol)
# define f(x), the model with the parameters set to the fitted values
f(x) = model(a=sol[0].rhs(),b=sol[1].rhs(),c=sol[2].rhs(),d=sol[3].rhs(),e=sol[4].rhs())
# create an empty plot object
a = plot([])
# add a plot of the model, with respect to x from -pi/2 to pi/2
a += plot(f(x),x,[-pi/2,pi/2])
# add a plot of the data, in red
a += list_plot(data,color='red')
show(a)
e = 0
for i in range(len(x)):
e += (f(x[i])-y[i])**2
print(e)
没有安装 S a g e M a t h SageMath SageMath可以使用网页版
有了精确的拟合结果,下面将使用四种传统的非线性拟合算法进行拟合,另外做了模拟退火算法的尝试可供改进。
G a u s s – N e w t o n Gauss–Newton Gauss–Newton算法[1]
G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法是通过对 N e w t o n Newton Newton函数优化方法的近似推导出来。因此, G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法的收敛速度在某些规律性条件下可以是二次的。一般来说(在较弱的条件下),收敛速度是线性的。
对于我们需要优化参数的函数 S = ∑ i = 1 m r i 2 ( β ) = ∑ i = 1 m ( y i − f ( β , x i ) ) 2 S=\sum\limits_{i=1}^mr_i^2(\beta)=\sum\limits_{i=1}^m(y_i-f(\beta,x_i))^2 S=i=1∑mri2(β)=i=1∑m(yi−f(β,xi))2, N e w t o n Newton Newton法优化其参数 β \beta β的递推关系为
β ( k + 1 ) = β ( k ) − H − 1 g \beta^{(k+1)}=\beta^{(k)}-H^{-1}g β(k+1)=β(k)−H−1g
其中, g g g表示 f f f关于 β \beta β的梯度, H H H为 S S S的 H e s s i a n Hessian Hessian矩阵
由 S = ∑ i = 1 m r i 2 S=\sum\limits_{i=1}^m r_i^2 S=i=1∑mri2,梯度和 H e s s i a n Hessian Hessian矩阵由下式导出
KaTeX parse error: Undefined control sequence: \part at position 30: …1}^m r_i\dfrac{\̲p̲a̲r̲t̲ ̲r_j}{\part \bet…
G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法是通过忽略二阶导数项(该表达式中的第二项)获得的。也就是说, H e s s i a n Hessian Hessian矩阵近似为
H j k ≈ 2 ∑ i = 1 m J i j J i k H_{jk}\approx 2\sum _{i=1}^{m}J_{ij}J_{ik} Hjk≈2i=1∑mJijJik
其中, J i j = ∂ r i ∂ β j J_{ij}=\dfrac{\partial r_i}{\partial \beta_{j}} Jij=∂βj∂ri为 J a c o b i Jacobi Jacobi矩阵的元素, J a c o b i Jacobi Jacobi矩阵 J J J为
KaTeX parse error: Undefined control sequence: \part at position 33: …} \left(\dfrac{\̲p̲a̲r̲t̲ ̲f}{\part \beta_…
当 r i r_i ri越接近 S S S的零点时,二阶导数项将越趋近于 0 0 0,于是我们可以将梯度与 H e s s i a n Hessian Hessian矩阵表示为
g = 2 J r T r H ≈ 2 J r T J r g=2J_r^Tr\\H\approx 2J_r^TJ_r g=2JrTrH≈2JrTJr
其中,残差 r r r为
r = ( y 1 − f ( β , x 1 ) ⋮ y m − f ( β , x m ) ) r=\begin{pmatrix} y_1-f(\beta,x_1)\\ \vdots\\ y_m-f(\beta,x_m) \end{pmatrix} r=⎝⎜⎛y1−f(β,x1)⋮ym−f(β,xm)⎠⎟⎞
代入 N e w t o n Newton Newton法的递推关系式,得到方程
β ( n + 1 ) = β ( n ) + Δ Δ = − ( J r T J r ) − 1 J r T r ⇔ ( J r T J r ) Δ = − J r T r \beta^{(n+1)}=\beta^{(n)}+\Delta\\ \Delta = -(J_r^TJ_r)^{-1}J_r^T r\Leftrightarrow(J_r^TJ_r)\Delta = -J_r^T r β(n+1)=β(n)+ΔΔ=−(JrTJr)−1JrTr⇔(JrTJr)Δ=−JrTr
另外,如果想要控制收敛速度,可以引入步长 α ≤ 1 \alpha\le 1 α≤1,将上式改为
β ( n + 1 ) = β ( n ) + α Δ \beta^{(n+1)}=\beta^{(n)}+\alpha \Delta β(n+1)=β(n)+αΔ
代码如下:
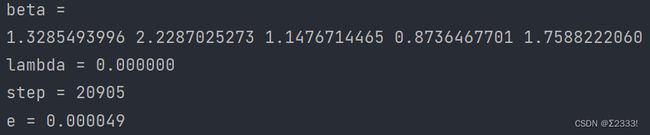
#include 由于 C / C + + C/C++ C/C++精度的问题,误差 e = ( ∑ i = 0 10 ( p ( x i ) − f ( x i ) ) 2 ) 1 2 e=(\sum\limits_{i=0}^{10}\left(p(x_i)-f(x_i))^2\right)^{\frac{1}{2}} e=(i=0∑10(p(xi)−f(xi))2)21最小只能达到0.000049
需要注意的是, G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法需要在保证能够忽略二阶导数项的情况下才能收敛到预期结果,具体需要满足以下条件之一:
1、 r i r_i ri很小,即需要在取最小值的点附近
2、拟合的目标函数只是“轻微”非线性的,因此 ∂ i a l 2 r i ∂ i a l β j ∂ i a l β k \dfrac {\partial ial ^{2}r_{i}}{\partial ial \beta _{j}\partial ial \beta_{k}} ∂ialβj∂ialβk∂ial2ri相对较小
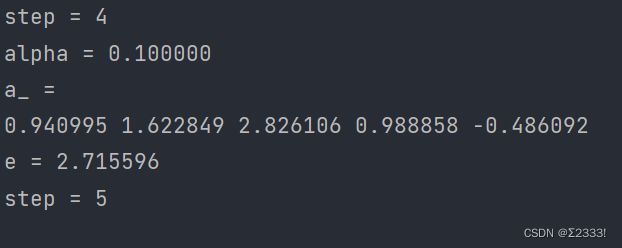
例如将上述代码中的beta[] = {1.3, 2.2, 1.1, 0.9, 1.8}改为beta[] = {0.1, 0.1, 0.1, 0.1, 0.1}可得

显然这不是我们想要的结果,或者说,收敛到了一个局部最优解,于是基于此,我们可以使用局部优化算法,例如模拟退火、遗传算法等进行改进,这将在下文提到。
L e v e n b e r g – M a r q u a r d t Levenberg–Marquardt Levenberg–Marquardt算法[2]
L e v e n b e r g – M a r q u a r d t Levenberg–Marquardt Levenberg–Marquardt算法也被称为阻尼最小二乘,用于解决非线性最小二乘问题, L e v e n b e r g – M a r q u a r d t Levenberg–Marquardt Levenberg–Marquardt算法是 G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法的改进算法,在许多情况下,即使它开始时离最终最小值很远,它也能找到解决方案,但对于对于表现良好的函数和合理的起始参数, L e v e n b e r g – M a r q u a r d t Levenberg–Marquardt Levenberg–Marquardt算法往往比 G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法慢。 L e v e n b e r g – M a r q u a r d t Levenberg–Marquardt Levenberg–Marquardt算法也可以看作是使用信任域方法的 G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法。
需要注意的是, L e v e n b e r g – M a r q u a r d t Levenberg–Marquardt Levenberg–Marquardt算法与其他迭代优化算法一样,仍然只能找到局部最优解,但相比于 G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法效果更好。
L e v e n b e r g – M a r q u a r d t Levenberg–Marquardt Levenberg–Marquardt算法对于 G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法改进的地方在于,将 ( J r T J r ) Δ = − J r T r (J_r^TJ_r)\Delta = -J_r^T r (JrTJr)Δ=−JrTr替换成
( J r T J r + λ I ) Δ = − J r T r (J_r^TJ_r+\lambda I)\Delta = -J_r^T r (JrTJr+λI)Δ=−JrTr
其中, λ \lambda λ为阻尼因子, I I I为单位向量
阻尼因子 λ ≥ 0 \lambda\ge 0 λ≥0每次迭代都会调整,如果 S S S的减小速度快,则使 λ \lambda λ减小,使算法更接近于 G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法;如果迭代没有充分减少残差 r r r,则使 λ \lambda λ增大,从而使算法更接近于梯度下降方向。
关于阻尼因子 λ \lambda λ的选择,在迭代开始前,选择一个初始值 λ 0 \lambda_0 λ0,并引入一个迭代因子 ν > 1 \nu>1 ν>1,采用延迟满足的策略,即在每个上坡(误差增大)步骤将 λ \lambda λ减少少量,下坡(误差减小)步骤将 λ \lambda λ增加大量,该策略背后的想法是避免在优化开始时过快地下坡,从而限制未来迭代中可用的步骤,减慢收敛速度。在大多数情况下,增加2倍和减少3倍已被证明是有效的,而对于大型问题,更极端的值可以更好地工作,增加1.5倍和减少5倍。
代码如下:
#include
#include
#include
#include "vector_matrix.h"
void trace(int n, double **A, double **trA);
void construct_J(int m, double *beta, double *x, double **J) {
// 构造Jacobi矩阵
int i;
for (i = 0; i < m; i++) {
J[i][0] = 1.0;
}
for (i = 0; i < m; i++) {
J[i][1] = sin(beta[2] * x[i]);
}
for (i = 0; i < m; i++) {
J[i][2] = beta[1] * x[i] * cos(beta[2] * x[i]);
}
for (i = 0; i < m; i++) {
J[i][3] = cos(beta[4] * x[i]);
}
for (i = 0; i < m; i++) {
J[i][4] = (-beta[3] * x[i] * sin(beta[4] * x[i]));
}
}
void construct_r(int m, double *x, double *y, double *beta, double *r) {
// 构造r
int i;
for (i = 0; i < m; i++) {
r[i] = y[i] - (beta[0] + beta[1] * sin(beta[2] * x[i]) + beta[3] * cos(beta[4] * x[i]));
}
}
void LMAlgorithm(int m, int n, double *beta, double alpha, double **J, double *r, double lambda) {
/*
JT 为J的转置
JTJ 为JT*J
JTr 为JT*r
delta_beta 为Δ
trJTJ 为对角线元素为JTJ对角线元素,其他元素均为0的矩阵
*/
double **JT, **JTJ, **trJTJ;
double *JTr, *delta_beta;
int i, j;
JT = (double **) malloc(sizeof(double *) * n);
for (i = 0; i < n; i++) {
JT[i] = (double *) malloc(sizeof(double) * m);
}
JTJ = (double **) malloc(sizeof(double *) * n);
for (i = 0; i < n; i++) {
JTJ[i] = (double *) malloc(sizeof(double) * n);
}
trJTJ = (double **) malloc(sizeof(double *) * n);
for (i = 0; i < n; i++) {
trJTJ[i] = (double *) malloc(sizeof(double) * n);
}
JTr = (double *) malloc(n * sizeof(double));
delta_beta = (double *) malloc(n * sizeof(double));
matrix_tranform(m, n, J, JT);
matrix_times_matrix(n, m, n, JT, J, JTJ);
trace(n, JTJ, trJTJ);
num_times_matrix(n, n, trJTJ, lambda, trJTJ);
matrix_add_matrix(n, n, JTJ, trJTJ, JTJ);
matrix_times_vector(n, m, JT, r, JTr);
solve_linear(n, JTJ, JTr, delta_beta);
num_times_vector(n, delta_beta, alpha, delta_beta);
vector_add_vector(n, beta, delta_beta, beta);
free(JT);
free(JTJ);
free(trJTJ);
free(JTr);
free(delta_beta);
}
double cal_error(int m, double *beta, double *x, double *y) {
// 计算误差
int i, j;
double e = 0.0, t;
for (i = 0; i < m; i++) {
t = beta[0] + beta[1] * sin(beta[2] * x[i]) + beta[3] * cos(beta[4] * x[i]);
e += pow(t - y[i], 2);
}
return sqrt(e);
}
int main() {
/*
该程序用于使用Levenberg–Marquardt算法解决非线性最小二乘问题
p(x)=a_0+a_1*sin(a_2*x)+a_3*cos(a_4*x)
m 表示数据数目
n 表示参数数目
x 表示拟合点坐标
y 表示拟合点函数值
beta 表示参数向量
J 为Jacobi矩阵
r 为残差
alpha 表示梯度下降速率
lambda 表示阻尼因子
nu1,nu2 表示迭代因子
eps 表示可允许误差
e 表示误差
d 表示前后两次误差之差
delta 表示d可允许最大值
*/
int m = 11, n = 5;
double x[] = {-1, -0.8, -0.6, -0.4, -0.2, 0.0, 0.2, 0.4, 0.6, 0.8, 1.0};
double y[] = {-0.8669, -0.2997, 0.3430, 1.0072, 1.6416, 2.2022, 2.6558, 2.9823, 3.1755, 3.2416, 3.1974};
double beta[] = {0.1, 0.1, 0.1, 0.1, 0.1};
// double beta[] = {1.3, 2.2, 1.1, 0.9, 1.8};
double **J;
double *r;
double alpha = 0.001, eps = 0.00001, e = 10, delta = 1e-16, d = 1, e_ = 0;
double lambda = 0.1, nu1 = 2.0, nu2 = 3.0;
int step = 0;
int i, j;
// J是一个m*n矩阵
J = (double **) malloc(sizeof(double *) * m);
for (i = 0; i < m; i++) {
J[i] = (double *) malloc(sizeof(double) * n);
}
r = (double *) malloc(m * sizeof(double));
while (e > eps && fabs(d) > delta) {
construct_J(m, beta, x, J);
construct_r(m, x, y, beta, r);
LMAlgorithm(m, n, beta, alpha, J, r, lambda);
e = cal_error(m, beta, x, y);
output(m, n, beta);
d = e_ - e;
e_ = e;
if (d > 0) {
// 下坡减少大量参数
lambda /= nu2;
} else {
// 上坡增加大量参数
lambda *= nu1;
}
step += 1;
}
free(J);
free(r);
}
void trace(int n, double **A, double **trA) {
// 构造对角线元素为A的对角线元素,其他元素均为0的矩阵
int i, j;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
if (i != j) {
trA[i][j] = 0;
} else {
trA[i][j] = A[i][j];
}
}
}
}
当beta取近似值,alpha取1.0,结果为
将上述代码中的beta[] = {1.3, 2.2, 1.1, 0.9, 1.8}改为beta[] = {0.1, 0.1, 0.1, 0.1, 0.1},结果为

发现算法并没有收敛,尝试减小alpha
若alpha取0.001,结果为
虽然用了较多的步数,但结果接近于理想的拟合结果,可见 L e v e n b e r g – M a r q u a r d t Levenberg–Marquardt Levenberg–Marquardt算法在一定程度上确实优于 G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法。
Q u a s i − N e w t o n Quasi-Newton Quasi−Newton方法(准 N e w t o n Newton Newton法/拟 N e w t o n Newton Newton法)[3]
准 N e w t o n Newton Newton法是用于寻找零点或函数的局部最大值和最小值的方法,作为 N e w t o n Newton Newton法的替代方法。完整的 N e w t o n Newton Newton法需要用到 J a c o b i Jacobi Jacobi矩阵寻找零点或用到 H e s s i a n Hessian Hessian矩阵来寻找极值,如果 J a c o b i Jacobi Jacobi或 H e s s i a n Hessian Hessian矩阵不可用或在每次迭代时计算过于昂贵,则可以使用准 N e w t o n Newton Newton法。
在优化算法中,寻找标量值函数的最小值或最大值只不过是寻找该函数梯度的零点。因此,准 N e w t o n Newton Newton法可以很容易地用于寻找函数的极值。换句话说,如果 g g g是 f f f的梯度,然后搜索向量值函数 g g g的零点,对应于寻找标量值函数 f f f的极值, g g g的 J a c o b i Jacobi Jacobi矩阵现在变成了 f f f的 H e s s i a n Hessian Hessian矩阵,主要区别在于 H e s s i a n Hessian Hessian矩阵是一个对称矩阵。大多数用于优化的准 N e w t o n Newton Newton法都利用了这个特性。
准 N e w t o n Newton Newton法是基于 N e w t o n Newton Newton法找到函数的驻点,其中梯度为0。 N e w t o n Newton Newton法假设函数可以在最优值附近的区域内局部近似为二次函数,并使用一阶导和二阶导来找到住点。在更高维度上, N e w t o n Newton Newton法使用梯度和二阶导数的 H e s s i a n Hessian Hessian矩阵来使函数最小化。
在准 N e w t o n Newton Newton法中,不需要计算 H e s s i a n Hessian Hessian矩阵。而是通过分析连续的梯度向量来更新 H e s s i a n Hessian Hessian矩阵。准 N e w t o n Newton Newton法是对多维问题求一阶导数根的割线方法的推广。在多维函数中,割线方程是欠定的,准 N e w t o n Newton Newton法在约束解的方式上有所不同,通常是通过对 H e s s i a n Hessian Hessian矩阵的当前估计添加简单的低秩矩阵来更新。
第一个准 N e w t o n Newton Newton法是由在Argonne National Laboratory工作的物理学家William C. Davidon提出的。他在 1959 年开发了第一个准 N e w t o n Newton Newton法:DFP 更新公式,后来在 1963 年被 Fletcher 和 Powell 推广,但今天很少使用。目前最常见的准牛顿算法是SR1 公式(用于“对称秩一”的情形)、BHHH方法、广泛使用的BFGS 方法(由 Broyden、Fletcher、Goldfarb 和 Shanno 在 1970 年独立提出),以及它的低-内存扩展L-BFGS。Broyden family 是 DFP 和 BFGS 方法的线性组合。
SR1公式不保证更新矩阵保持正定性,可用于不定问题。Broyden 方法不需要更新矩阵是对称的,它用于通过更新 J a c o b i Jacobi Jacobi矩阵(而不是 H e s s i a n Hessian Hessian矩阵)来找到一般方程组的根(而不是梯度)。
与 N e w t o n Newton Newton法相比,准 N e w t o n Newton Newton法的主要优点之一是 H e s s i a n Hessian Hessian矩阵(或者,在准 N e w t o n Newton Newton法的情况下,它的近似值) B B B不需要求逆, N e w t o n Newton Newton法及其衍生方法(例如内点法)需要对 H e s s i a n Hessian Hessian矩阵进行求逆,这通常通过求解线性方程组来实现,并且通常成本很高。相比之下,准 N e w t o n Newton Newton法通常会直接生成 B − 1 B^{-1} B−1。
准 N e w t o n Newton Newton法与 N e w t o n Newton Newton法相同,使用二阶近似来寻找 f ( x ) f(x) f(x)的最小值, f ( x ) f(x) f(x)的二阶泰勒展开为
f ( x k + Δ x ) ≈ f ( x k ) + ∇ f ( x k ) T Δ x + 1 2 Δ x T B Δ x f(x_k+\Delta x)\approx f(x_k)+\nabla f(x_k)^T \Delta x+\dfrac{1}{2}\Delta x^TB\Delta x f(xk+Δx)≈f(xk)+∇f(xk)TΔx+21ΔxTBΔx
其中 ∇ f \nabla f ∇f为梯度, B B B为 H e s s i a n Hessian Hessian矩阵的近似矩阵。对上式两端对于 Δ x \Delta x Δx求梯度可得
∇ f ( x k + Δ x ) ≈ ∇ f ( x k ) + B Δ x \nabla f(x_k+\Delta x)\approx \nabla f(x_k)+B\Delta x ∇f(xk+Δx)≈∇f(xk)+BΔx
优化后,上式左侧的梯度为0,则
Δ x = − B − 1 ∇ f ( x k ) \Delta x=-B^{-1}\nabla f(x_k) Δx=−B−1∇f(xk)
此时 H e s s i a n Hessian Hessian矩阵的近似矩阵 B B B满足
∇ f ( x k + Δ x ) = ∇ f ( x k ) + B Δ x \nabla f(x_k+\Delta x)= \nabla f(x_k)+B\Delta x ∇f(xk+Δx)=∇f(xk)+BΔx
这即是割线方程
对于 B B B的初始值的选择,一般设 B 0 = β I B_0=\beta I B0=βI可以快速收敛,尽管对于 β \beta β的选取没有一个通用的策略
接下来,我们采用BFGS方法[4]进行求解,需要注意的是,为了避免进行任何的矩阵求逆运算,在经过改进的BFGS方法中, B k B_k Bk表示 H e s s i a n Hessian Hessian矩阵的逆矩阵
算法如下:
从初始的 x 0 x_0 x0和近似 H e s s i a n Hessian Hessian矩阵的逆矩阵 B 0 B_0 B0开始进行迭代
1、通过计算 p k = − B k ∇ f ( x ) p_k=-B_k\nabla f(x) pk=−Bk∇f(x)来获取方向向量 p k p_k pk
2、执行一维优化(线搜索)以找到朝着步骤1的方向的合适的步长 α k \alpha_k αk, α k \alpha_k αk需满足 W o l f e Wolfe Wolfe条件[5]:
Ⅰ f ( x k + α k p k ) ≤ f ( x k ) + c 1 α k p k T ∇ f ( x k ) f(x_k+\alpha_k p_k)\le f(x_k)+c_1\alpha_k p_k^T\nabla f(x_k) f(xk+αkpk)≤f(xk)+c1αkpkT∇f(xk)
Ⅱ − p k T ∇ f ( x k + α k p k ) ≤ − c 2 p k T ∇ f ( x k ) -p_k^T \nabla f(x_k+\alpha_k p_k)\le -c_2p_k^T\nabla f(x_k) −pkT∇f(xk+αkpk)≤−c2pkT∇f(xk)
其中 0 < c 1 < c 2 < 1 0
3、设 s k = α k p k s_k=\alpha_k p_k sk=αkpk,并更新 x k + 1 = x k + s k x_{k+1}=x_k+s_k xk+1=xk+sk
4、 y k = ∇ f ( x k + 1 ) − ∇ f ( x k ) y_k=\nabla f(x_{k+1})-\nabla f(x_{k}) yk=∇f(xk+1)−∇f(xk)
5、 B k + 1 = B k + ( s k T y k + y k T B k y k ) ( s k s k T ) ( s k T y k ) 2 − B k y k s k T + s k y k T B k s k T y k B_{k+1}=B_{k}+{\dfrac {({s}_{k}^{T}{y}_{k}+{ y}_{k}^{T}B_{k}{y}_{k})({s}_{k}{s}_{k}^{{T}})}{({s}_{k}^{{T}}{y}_{k})^{2}}}-{\dfrac {B_{k}{y}_{k}{s}_{k}^{{T}}+{s}_{k}{y}_{k}^{{T}}B_{k}}{{s}_{k}^{{T}}{y}_{k}}} Bk+1=Bk+(skTyk)2(skTyk+ykTBkyk)(skskT)−skTykBkykskT+skykTBk
其中,第5步的推导用到了 S h e r m a n – M o r r i s o n Sherman–Morrison Sherman–Morrison公式,这里不再赘述
代码如下:
#include
#include
#include
#include "vector_matrix.h"
double cal_error(int m, double *a, double *x, double *y);
double f(int i, double *a, double *x) {
return a[0] + a[1] * sin(a[2] * x[i]) + a[3] * cos(a[4] * x[i]);
}
void nabla(int m, int n, double *a, double *x, double *y, double *nf) {
// 计算f的梯度
int i, j;
for (i = 0; i < n; i++) {
nf[i] = 0;
}
for (i = 0; i < m; i++) {
nf[0] += 2 * (f(i, a, x) - y[i]);
nf[1] += 2 * sin(a[2] * x[i]) * (f(i, a, x) - y[i]);
nf[2] += 2 * a[1] * x[i] * cos(a[2] * x[i]) * (f(i, a, x) - y[i]);
nf[3] += 2 * cos(a[4] * x[i]) * (f(i, a, x) - y[i]);
nf[4] += (-2 * a[3] * x[i] * sin(a[4] * x[i]) * (f(i, a, x) - y[i]));
}
}
double get_alpha(int m, int n, double *a, double *x, double *y, double *p) {
/*
寻找满足Wolfe条件的alpha
l1 为Wolfe条件1的左侧
r1 为Wolfe条件1的右侧
l2 为Wolfe条件2的左侧
r2 为Wolfe条件2的右侧
ap 为alpha_k*p_k
xap 为x_k+alpha_k*p_k
nf 为\nabla f(x_k)
nf_ 为\nabla f(x_k+alpha_k*p_k)
*/
double alpha = 1, c1 = 1e-4, c2 = 0.9;
double l1 = 0, r1 = 0, l2 = 0, r2 = 0;
double *ap, *xap, *nf, *nf_;
int i, j;
ap = (double *) malloc(sizeof(double) * n);
xap = (double *) malloc(sizeof(double) * n);
nf = (double *) malloc(sizeof(double) * n);
nf_ = (double *) malloc(sizeof(double) * n);
num_times_vector(n, p, alpha, ap);
vector_add_vector(n, a, ap, xap);
nabla(m, n, a, x, y, nf);
nabla(m, n, xap, x, y, nf_);
for (i = 0; i < m; i++) {
l1 += pow(f(i, xap, x) - y[i], 2);
}
for (i = 0; i < m; i++) {
r1 += pow(f(i, a, x) - y[i], 2);
}
r1 += c1 * vector_dot_vector(n, ap, nf);
l2 = -vector_dot_vector(n, p, nf_);
r2 = -c2 * vector_dot_vector(n, p, nf);
while ((l1 - r1 > 1e-6) || (l2 - r2 > 1e-6)) {
l1 = 0;
r1 = 0;
alpha *= 0.1;
num_times_vector(n, p, alpha, ap);
vector_add_vector(n, a, ap, xap);
nabla(m, n, a, x, y, nf);
nabla(m, n, xap, x, y, nf_);
num_times_vector(n, p, alpha, ap);
vector_add_vector(n, a, ap, xap);
nabla(m, n, a, x, y, nf);
nabla(m, n, xap, x, y, nf_);
for (i = 0; i < m; i++) {
l1 += pow(f(i, xap, x) - y[i], 2);
}
for (i = 0; i < m; i++) {
r1 += pow(f(i, a, x) - y[i], 2);
}
r1 += c1 * vector_dot_vector(n, ap, nf);
l2 = -vector_dot_vector(n, p, nf_);
r2 = -c2 * vector_dot_vector(n, p, nf);
}
free(ap);
free(xap);
free(nf);
free(nf_);
return alpha;
}
void QNMethod(int m, int n, double beta, double *a, double *x, double *y, double eps) {
/*
nf 表示f(x_k)
nf_ 表示f(x_{k+1})
p 表示方向向量
s 表示a_k*p_k
a_ 表示x_{k+1}
yk 表示y_k=\nabla f(x_{k+1})-\nabla f(x_{k})
ss 表示s_k*s_k^T
Bys 表示B_k*y_k
syB 表示s_k*y_k^T*B_k
yB 表示y_k^T*B_k
By 表示B_k*y_k
B 表示B_k
B_ 表示B_{k+1}
alpha 表示\alpha_k
e 表示误差
*/
double *nf, *nf_, *p, *s, *a_, *yk;
double **ss, **Bys, **syB;
double *yB, *By;
double sy, yBy;
double **B, **B_;
double alpha, e = 1.0;
int i, j, step = 0;
B = (double **) malloc(sizeof(double *) * n);
for (i = 0; i < n; i++) {
B[i] = (double *) malloc(sizeof(double) * n);
}
B_ = (double **) malloc(sizeof(double *) * n);
for (i = 0; i < n; i++) {
B_[i] = (double *) malloc(sizeof(double) * n);
}
ss = (double **) malloc(sizeof(double *) * n);
for (i = 0; i < n; i++) {
ss[i] = (double *) malloc(sizeof(double) * n);
}
Bys = (double **) malloc(sizeof(double *) * n);
for (i = 0; i < n; i++) {
Bys[i] = (double *) malloc(sizeof(double) * n);
}
syB = (double **) malloc(sizeof(double *) * n);
for (i = 0; i < n; i++) {
syB[i] = (double *) malloc(sizeof(double) * n);
}
nf = (double *) malloc(sizeof(double) * n);
nf_ = (double *) malloc(sizeof(double) * n);
p = (double *) malloc(sizeof(double) * n);
s = (double *) malloc(sizeof(double) * n);
a_ = (double *) malloc(sizeof(double) * n);
yk = (double *) malloc(sizeof(double) * n);
yB = (double *) malloc(sizeof(double) * n);
By = (double *) malloc(sizeof(double) * n);
for (i = 0; i < n; i++) {
B[i][i] = beta;
}
while (e > eps) {
step += 1;
// step1: 计算p_k
nabla(m, n, a, x, y, nf);
matrix_times_vector(n, n, B, nf, p);
num_times_vector(n, p, -1.0, p);
// step2: 计算alpha
alpha = get_alpha(m, n, a, x, y, p);
// step3: 计算x_{k+1}
num_times_vector(n, p, alpha, s);
vector_add_vector(n, a, s, a_);
e = cal_error(m, a_, x, y);
// step4: 计算y_k
nabla(m, n, a_, x, y, nf_);
vector_minus_vector(n, nf_, nf, yk);
// step5: 计算B_{k+1}
sy = vector_dot_vector(n, s, yk);
matrix_times_vector(n, n, B, yk, By);
yBy = vector_dot_vector(n, yk, By);
vector_times_vector(n, s, s, ss);
vector_times_vector(n, By, s, Bys);
vector_times_matrix(n, n, B, yk, yB);
vector_times_vector(n, s, yB, syB);
// 计算第二项
num_times_matrix(n, n, ss, sy + yBy, ss);
matrix_divide_num(n, n, ss, pow(sy, 2), ss);
// 计算第三项
matrix_add_matrix(n, n, Bys, syB, syB);
matrix_divide_num(n, n, syB, sy, syB);
// 计算B_{k+1}
matrix_add_matrix(n, n, B, ss, B_);
matrix_minus_matrix(n, n, B_, syB, B_);
// 更新数据
copy_vector(n, a_, a);
copy_matrix(n, n, B_, B);
}
free(B);
free(B_);
free(ss);
free(Bys);
free(syB);
free(nf);
free(nf_);
free(p);
free(s);
free(a_);
free(yk);
free(yB);
free(By);
}
int main() {
/*
该程序用于使用准牛顿法解决非线性最小二乘问题
p(x)=a_0+a_1*sin(a_2*x)+a_3*cos(a_4*x)
m 表示数据数目
n 表示参数数目
x 表示拟合点坐标
y 表示拟合点函数值
a 表示参数向量
eps 表示可允许误差
*/
int m = 11, n = 5;
double x[] = {-1, -0.8, -0.6, -0.4, -0.2, 0.0, 0.2, 0.4, 0.6, 0.8, 1.0};
double y[] = {-0.8669, -0.2997, 0.3430, 1.0072, 1.6416, 2.2022, 2.6558, 2.9823, 3.1755, 3.2416, 3.1974};
// double a[] = {0.1, 0.1, 0.1, 0.1, 0.1};
double a[] = {1.3, 2.2, 1.1, 0.9, 1.8};
double beta = 1.0, eps = 0.00001;
QNMethod(m, n, beta, a, x, y, eps);
}
double cal_error(int m, double *a, double *x, double *y) {
int i, j;
double e = 0.0, t;
for (i = 0; i < m; i++) {
t = a[0] + a[1] * sin(a[2] * x[i]) + a[3] * cos(a[4] * x[i]);
e += pow(t - y[i], 2);
}
return sqrt(e);
}
结果为
需要注意的是,关于第二步进行线搜索寻找 α k \alpha_k αk,由于结果不需要太精确,以上代码采用直接搜索[6]的方法,每次迭代执行alpha *= 0.1,当然也可以用简单有效的黄金分割搜索,即phi=(1 + sqrt(5)) / 2; alpha /= phi;;终止条件也没有设成l1 <= r1 && l2 <= r2,而是(l1 - r1 <=- 1e-6) && (l2 - r2 <= 1e-6)
将上述代码中的beta[] = {1.3, 2.2, 1.1, 0.9, 1.8}改为beta[] = {0.1, 0.1, 0.1, 0.1, 0.1},结果为
在step=5时,无法找到符合条件的alpha
N e l d e r – M e a d Nelder–Mead Nelder–Mead方法[7][8]
N e l d e r − M e a d Nelder-Mead Nelder−Mead方法(也称为下坡单纯形法、变形虫法、单纯形搜索算法或多面体法)是一种用于在多维空间中找到目标函数最小值或最大值的数值方法。不同于上述三种算法, N e l d e r − M e a d Nelder-Mead Nelder−Mead方法是一种基于函数比较的直接搜索方法,通常应用于不知道导数的非线性优化问题。
几何学上,单纯形或者n-单纯形是和三角形类似的 n n n维几何体。[9]
以下是该方法的可视化展示:
以下为 N e l d e r − M e a d Nelder-Mead Nelder−Mead方法的一种变体:
假设我们正在尝试最小化的函数为 f ( x ) f(x) f(x),其中 x ∈ R n x\in\R^{n} x∈Rn,目前有测试点 x 1 . x 2 , ⋯ , x n + 1 x_1.x_2, \cdots,x_{n+1} x1.x2,⋯,xn+1
1、Order
根据测试点的函数值排序,使得
f ( x 1 ) ≤ f ( x 2 ) ≤ ⋯ ≤ f ( x n + 1 ) f(x_1)\le f(x_2)\le \cdots\le f(x_{n+1}) f(x1)≤f(x2)≤⋯≤f(xn+1)
检查是否满足终止条件(Termination),若满足,则输出结果
2、计算测试点 x 1 . x 2 , ⋯ , x n x_1.x_2, \cdots,x_{n} x1.x2,⋯,xn的质心(几何中心) x o = 1 n ∑ i = 1 n x i x_o=\dfrac{1}{n}\sum\limits_{i=1}^n x_i xo=n1i=1∑nxi
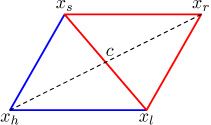
3、Reflection
计算反射点 x r = x o + α ( x o − x n + 1 ) , α > 0 x_r=x_o+\alpha(x_o-x_{n+1}),\alpha>0 xr=xo+α(xo−xn+1),α>0
如果反射点 x r x_r xr优于次最佳点 x n x_{n} xn,但不优于最佳点 x 1 x_1 x1,即 f ( x 1 ) ≤ f ( x r ) < f ( x n ) f(x_1)\le f(x_r)
通过用反射点 x r x_r xr替换最差点 x n + 1 x_{n+1} xn+1获得一个新的单纯形,转到步骤1
如下图
4、Expansion
如果反射点 x o x_o xo是目前为止最好的点,即 f ( x r ) < f ( x 1 ) f(x_r)
计算扩展点 x e = x o + γ ( x r − x o ) , γ > 1 x_e=x_o+\gamma(x_r-x_o),\gamma>1 xe=xo+γ(xr−xo),γ>1
如果扩展点 x e x_e xe比反射点 x r x_r xr好,即 f ( x e ) < f ( x r ) f(x_e)
通过用扩展点 x e x_e xe替换最差点 x n + 1 x_{n+1} xn+1获得一个新的单纯形,转到步骤1
否则
通过用反射点 x r x_r xr替换最差点 x n + 1 x_{n+1} xn+1获得一个新的单纯形,转到步骤1
如下图
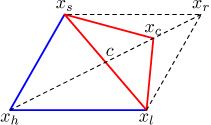
5、Contraction
此时已经确定有 f ( x r ) ≥ f ( x n ) f(x_r)\ge f(x_n) f(xr)≥f(xn)
如果 f ( x r ) < f ( x n + 1 ) f(x_r)
计算外部收缩点 x c = x o + ρ ( x r − x o ) , 0 < ρ ≤ 0.5 x_c=x_o+\rho(x_r-x_o),0<\rho\le0.5 xc=xo+ρ(xr−xo),0<ρ≤0.5
如果收缩点 x c x_c xc优于反射点 x r x_r xr,即 f ( x c ) < f ( x r ) f(x_c)
通过用收缩点 x c x_c xc替换最差点 x n + 1 x_{n+1} xn+1获得一个新的单纯形,转到步骤1
否则
跳转到步骤6
如下图
如果 f ( x r ) ≥ f ( x n + 1 ) f(x_r)\ge f(x_{n+1}) f(xr)≥f(xn+1),则
计算内部收缩点 x c = x o + ρ ( x n + 1 − x o ) , 0 < ρ ≤ 0.5 x_c=x_o+\rho(x_{n+1}-x_o),0<\rho\le0.5 xc=xo+ρ(xn+1−xo),0<ρ≤0.5
如果收缩点 x c x_c xc优于最差点 x n + 1 x_{n+1} xn+1,即 f ( x c ) < f ( x n + 1 ) f(x_c)
通过用收缩点 x c x_c xc替换最差点 x n + 1 x_{n+1} xn+1获得一个新的单纯形,转到步骤1
否则
跳转到步骤6
如下图
6、Shrink
用 x i = x 1 + σ ( x i − x 1 ) x_i=x_1+\sigma(x_i-x_1) xi=x1+σ(xi−x1)替换除最佳点 x 1 x_{1} x1以外的所有点,回到步骤1
如下图
注: α , β , ρ , σ \alpha,\beta,\rho,\sigma α,β,ρ,σ分别为reflection, expansion, contraction, shrink系数,标准值分别为 α = 1 , β = 2 , ρ = 1 / 2 , σ = 1 / 2 \alpha=1,\beta=2,\rho=1/2,\sigma=1/2 α=1,β=2,ρ=1/2,σ=1/2
代码如下:
#include
#include
#include
#include
#include "vector_matrix.h"
double cal_error(int m, double *beta, double *x, double *y);
void order(int m, int n, double **A, double *x, double *y);
void cal_centroid(int n, double **A, double *c);
void construct_A(int n, double *beta, double **A) {
// 随机生成测试点,构造测试点矩阵A
int i, j;
double range = 0.05;
for (i = 0; i < n + 1; i++) {
for (j = 0; j < n; j++) {
A[i][j] = ((rand() % ((int) (2 * range * 1e6 + 1))) + (beta[j] - range) * 1e6) / 1e6;
}
}
}
void reflection(int n, double **A, double *xo, double *xr) {
double alpha = 1.0;
double *t;
int i;
t = (double *) malloc(sizeof(double) * n);
for (i = 0; i < n; i++) {
xr[i] = 0;
}
vector_minus_vector(n, xo, A[n], t);
num_times_vector(n, t, alpha, t);
vector_add_vector(n, xo, t, xr);
free(t);
}
void expansion(int n, double *xo, double *xr, double *xe) {
double gama = 2.0;
double *t;
int i;
t = (double *) malloc(sizeof(double) * n);
for (i = 0; i < n; i++) {
xe[i] = 0;
}
vector_minus_vector(n, xr, xo, t);
num_times_vector(n, t, gama, t);
vector_add_vector(n, xo, t, xe);
free(t);
}
void shrink(int n, double **A) {
double sigma = 0.5;
double *t;
int i;
t = (double *) malloc(sizeof(double) * n);
for (i = 1; i < n + 1; i++) {
vector_minus_vector(n, A[i], A[0], t);
num_times_vector(n, t, sigma, t);
vector_add_vector(n, A[0], t, A[i]);
}
free(t);
}
void contraction(int m, int n, double **A, double *xo, double *xr, double *xc, double *x, double *y) {
double rho = 0.5;
double *t;
int i;
t = (double *) malloc(sizeof(double) * n);
for (i = 0; i < n; i++) {
xc[i] = 0;
}
if (cal_error(m, xr, x, y) < cal_error(m, A[n], x, y)) {
printf("f(xr)=f(xn+1)\n");
vector_minus_vector(n, A[n], xo, t);
num_times_vector(n, t, rho, t);
vector_add_vector(n, xo, t, xc);
if (cal_error(m, xc, x, y) < cal_error(m, A[n], x, y)) {
copy_vector(n, xc, A[n]);
printf("f(xc)=f(xn+1)\n");
}
}
free(t);
}
void NMMethod(int m, int n, double **A, double *beta, double *x, double *y, double eps) {
double *xo, *xr, *xe, *xc;
double e = 1.0;
int i, j, step = 0;
xo = (double *) malloc(sizeof(double) * n);
xr = (double *) malloc(sizeof(double) * n);
xe = (double *) malloc(sizeof(double) * n);
xc = (double *) malloc(sizeof(double) * n);
construct_A(n, beta, A);
order(m, n, A, x, y);
while (e > eps && fabs((cal_error(m, A[0], x, y) - cal_error(m, A[n], x, y))) > 1e-14) {
step += 1;
order(m, n, A, x, y);
e = cal_error(m, A[0], x, y);
if (e < eps) {
break;
}
cal_centroid(n, A, xo);
reflection(n, A, xo, xr);
if (cal_error(m, A[0], x, y) <= cal_error(m, xr, x, y) &&
cal_error(m, xr, x, y) < cal_error(m, A[n - 1], x, y)) {
copy_vector(n, xr, A[n]);
printf("f(x1)<=f(xr)=f(xr)\n");
copy_vector(n, xr, A[n]);
continue;
}
} else {
printf("f(xr)>=f(xn)\n");
contraction(m, n, A, xo, xr, xc, x, y);
}
}
free(xo);
free(xr);
free(xe);
free(xc);
}
int main() {
/*
该程序用于使用Nelder–Mead算法解决非线性最小二乘问题
p(x)=a_0+a_1*sin(a_2*x)+a_3*cos(a_4*x)
m 表示数据数目
n 表示参数数目
x 表示拟合点坐标
y 表示拟合点函数值
beta 表示参数向量
A 为(n+1)*n阶测试点矩阵
eps 表示可允许误差
e 表示误差
*/
int m = 11, n = 5;
double x[] = {-1, -0.8, -0.6, -0.4, -0.2, 0.0, 0.2, 0.4, 0.6, 0.8, 1.0};
double y[] = {-0.8669, -0.2997, 0.3430, 1.0072, 1.6416, 2.2022, 2.6558, 2.9823, 3.1755, 3.2416, 3.1974};
double beta[] = {1.3, 2.2, 1.1, 0.9, 1.8};
// double beta[] = {0.1, 0.1, 0.1, 0.1, 0.1};
double **A;
double eps = 0.00001;
int i, j;
srand((unsigned) time(NULL));
A = (double **) malloc(sizeof(double *) * (n + 1));
for (i = 0; i < n + 1; i++) {
A[i] = (double *) malloc(sizeof(double) * n);
}
NMMethod(m, n, A, beta, x, y, eps);
free(A);
}
double cal_error(int m, double *beta, double *x, double *y) {
// 计算误差
int i, j;
double e = 0.0, t;
for (i = 0; i < m; i++) {
t = beta[0] + beta[1] * sin(beta[2] * x[i]) + beta[3] * cos(beta[4] * x[i]);
e += pow(t - y[i], 2);
}
return sqrt(e);
}
void order(int m, int n, double **A, double *x, double *y) {
// 对A中向量进行排序
int i, j, k;
double *t;
t = (double *) malloc(n * sizeof(double));
for (i = 0; i < n; i++) {
k = i;
for (j = i + 1; j < n + 1; j++) {
if (cal_error(m, A[j], x, y) <= cal_error(m, A[k], x, y)) {
k = j;
}
}
if (k != i) {
copy_vector(n, A[i], t);
copy_vector(n, A[k], A[i]);
copy_vector(n, t, A[k]);
}
}
free(t);
}
void cal_centroid(int n, double **A, double *c) {
// 计算单纯形几何中心坐标
int i;
for (i = 0; i < n; i++) {
c[i] = 0;
}
for (i = 0; i < n; i++) {
vector_add_vector(n, A[i], c, c);
}
vector_divide_num(n, c, n, c);
}
结果为
将上述代码中的beta[] = {1.3, 2.2, 1.1, 0.9, 1.8}改为beta[] = {0.1, 0.1, 0.1, 0.1, 0.1},由于生成初始测试点组的随机性,有一定概率找到理想结果,一定概率收敛到局部最优解
成功结果:
失败结果:
模拟退火(simulated annealing)[10]
模拟退火 是一种概率逼近给定函数的全局最优值的技术。具体来说,在一个优化问题的大搜索空间中近似全局优化是一种启发式算法。它通常用于搜索空间离散的情况。对于在固定时间内找到近似全局最优值比找到精确局部最优值更重要的问题,模拟退火可能比梯度下降或分支定界等精确算法更可取。
基本迭代:在每一步,模拟退火的启发式都考虑当前状态 s s s的相邻状态 s ∗ s^* s∗,并概率性地决定将系统移动到状态 s ∗ s^* s∗还是保持原状态。
相邻状态:解决方案的优化涉及评估问题状态的邻居,这些邻居是通过保守地改变给定状态而产生的新状态。
接受概率:从当前状态 s s s转换到新状态 s n e w s_{new} snew的概率函数为 P ( e , e n e w , T ) P(e,e_{new},T) P(e,enew,T),这取决于能量 e = E ( s ) e=E(s) e=E(s)和 e n e w = E ( e n e w ) e_{new}=E(e_{new}) enew=E(enew)以及全局变量温度 T T T,能量较小的状态优于能量较大的状态,而概率函数 P P P可以防止当 e n e w e_{new} enew大于 e e e时陷入局部最值
伪代码如下:
以下为模仿局部搜索算法(求解八皇后问题)中的模拟退火的代码:
#include
#include
#include
#include
double cal_error(int m, double *a, double *x, double *y) {
// 计算误差
int i, j;
double e = 0.0, t;
for (i = 0; i < m; i++) {
t = a[0] + a[1] * sin(a[2] * x[i]) + a[3] * cos(a[4] * x[i]);
e += pow(t - y[i], 2);
}
return sqrt(e);
}
void simulated_annealing(int n, int m, double *a, double *a_, double T, double *x, double *y) {
/*
模拟退火
E 表示能量
probability 表示退火概率
choose 与probability表示保持状态概率
*/
int i, j;
double E, probability, choose;
double alpha = 0.001;
for (i = 0; i < n; i++) {
a_[i] = ((rand() % ((int) (2 * alpha * 1e6 + 1))) + (a[i] - alpha) * 1e6) / 1e6;
}
if (cal_error(m, a_, x, y) <= cal_error(m, a, x, y)) {
printf("new status:\n");
for (i = 0; i < n; i++) {
a[i] = a_[i];
printf("%lf ", a[i]);
}
printf("\n");
} else {
E = cal_error(m, a, x, y) - cal_error(m, a_, x, y);
probability = exp(E / T);
choose = rand() % 1000 / 1000;
if (choose <= probability) {
printf("E<0, new status:\n");
for (i = 0; i < n; i++) {
a[i] = a_[i];
printf("%lf ", a[i]);
}
}
printf("\n");
}
}
int main() {
/*
该程序用于使用模拟退火算法解决非线性最小二乘问题
p(x)=a_0+a_1*sin(a_2*x)+a_3*cos(a_4*x)
m 表示数据数目
n 表示参数数目
x 表示拟合点坐标
y 表示拟合点函数值
a 表示参数向量
e 表示误差
d 表示前后两次误差之差
delta 表示d可允许最大值
min_e 表示误差最小值
T 表示初始温度
*/
int m = 11, n = 5;
double x[] = {-1, -0.8, -0.6, -0.4, -0.2, 0.0, 0.2, 0.4, 0.6, 0.8, 1.0};
double y[] = {-0.8669, -0.2997, 0.3430, 1.0072, 1.6416, 2.2022, 2.6558, 2.9823, 3.1755, 3.2416, 3.1974};
double a[] = {1.3, 2.2, 1.1, 0.9, 1.8};
double *a_, *am;
double eps = 0.001, e = 1, min_e = 1;
double T = 5.0;
int i, step = 0;
srand((unsigned) time(NULL));
a_ = (double *) malloc(n * sizeof(double));
am = (double *) malloc(n * sizeof(double));
while (e > eps) {
step += 1;
printf("step = %d\n", step);
e = cal_error(m, a, x, y);
if (e < min_e) {
min_e = e;
for (i = 0; i < n; i++) {
am[i] = a[i];
}
}
printf("error:\n%lf\n", e);
simulated_annealing(n, m, a, a_, T, x, y);
T *= 0.99;
if (T < 1e-6) {
printf("T = 0, can't find a answer");
break;
}
}
printf("\nmin_e: %lf\n", min_e);
for (i = 0; i < n; i++) {
printf("%lf ", am[i]);
}
free(a_);
free(am);
}
显然,这不能得到正确的结果,因为八皇后问题的解是离散的,而我们要解决的确实连续解的问题
于是做了一些改进和尝试
以下代码为结合 G a u s s − N e w t o n Gauss-Newton Gauss−Newton算法的模拟退火算法的尝试:
#include
#include
#include
#include
#include "vector_matrix.h"
void construct_J(int m, double *beta, double *x, double **J) {
// 构造Jacobi矩阵J
int i;
for (i = 0; i < m; i++) {
J[i][0] = 1.0;
}
for (i = 0; i < m; i++) {
J[i][1] = sin(beta[2] * x[i]);
}
for (i = 0; i < m; i++) {
J[i][2] = beta[1] * x[i] * cos(beta[2] * x[i]);
}
for (i = 0; i < m; i++) {
J[i][3] = cos(beta[4] * x[i]);
}
for (i = 0; i < m; i++) {
J[i][4] = (-beta[3] * x[i] * sin(beta[4] * x[i]));
}
}
void construct_r(int m, double *x, double *y, double *beta, double *r) {
// 构造r
int i;
for (i = 0; i < m; i++) {
r[i] = y[i] - (beta[0] + beta[1] * sin(beta[2] * x[i]) + beta[3] * cos(beta[4] * x[i]));
}
}
void NGAlgorithm(int m, int n, double *beta, double alpha, double **J, double *r) {
/*
JT 为J的转置
JTJ 为JT*J
JTr 为JT*r
*/
double **JT, **JTJ;
double *JTr, *delta_beta;
int i, j;
JT = (double **) malloc(sizeof(double *) * n);
for (i = 0; i < n; i++) {
JT[i] = (double *) malloc(sizeof(double) * m);
}
JTJ = (double **) malloc(sizeof(double *) * n);
for (i = 0; i < n; i++) {
JTJ[i] = (double *) malloc(sizeof(double) * n);
}
JTr = (double *) malloc(n * sizeof(double));
delta_beta = (double *) malloc(n * sizeof(double));
matrix_tranform(m, n, J, JT);
matrix_times_matrix(n, m, n, JT, J, JTJ);
matrix_times_vector(n, m, JT, r, JTr);
solve_linear(n, JTJ, JTr, delta_beta);
num_times_vector(n, delta_beta, alpha, delta_beta);
vector_add_vector(n, beta, delta_beta, beta);
free(JT);
free(JTJ);
free(JTr);
free(delta_beta);
}
double cal_error(int m, double *beta, double *x, double *y) {
int i, j;
double e = 0.0, t;
for (i = 0; i < m; i++) {
t = beta[0] + beta[1] * sin(beta[2] * x[i]) + beta[3] * cos(beta[4] * x[i]);
e += pow(t - y[i], 2);
}
return sqrt(e);
}
void simulated_annealing(int n, int m, double *a, double T, double *x, double *y, double **J, double *r) {
/*
模拟退火
E 表示能量
probability 表示退火概率
choose 与probability表示保持状态概率
alpha 表示步长
gamma 表示随机相邻状态的范围
*/
int i, j;
double E, probability, choose;
double alpha = 0.1, gama = 0.5;
double *_a;
_a = (double *) malloc(n * sizeof(double));
for (i = 0; i < n; i++) {
_a[i] = a[i];
}
NGAlgorithm(m, n, a, alpha, J, r);
if (cal_error(m, a, x, y) <= cal_error(m, _a, x, y)) {
printf("new status:\n");
for (i = 0; i < n; i++) {
printf("%.10lf ", a[i]);
}
printf("\n");
} else {
E = cal_error(m, _a, x, y) - cal_error(m, a, x, y);
probability = exp(E / T);
choose = rand() % 1000 / 1000;
if (choose > probability) {
printf("E<0, new status:\n");
for (i = 0; i < n; i++) {
printf("%.10lf ", a[i]);
}
} else {
printf("E<0, old status:\n");
for (i = 0; i < n; i++) {
a[i] = ((rand() % ((int) (2 * gama * 1e6 + 1))) + (_a[i] - gama) * 1e6) / 1e6;
printf("%.10lf ", a[i]);
}
}
printf("\n");
}
free(_a);
}
int main() {
/*
该程序用于解决非线性最小二乘问题
p(x)=a_0+a_1*sin(a_2*x)+a_3*cos(a_4*x)
m 表示数据数目
n 表示参数数目
x 表示拟合点坐标
y 表示拟合点函数值
beta 表示参数向量
J 为Jacobi矩阵
r 为残差
alpha 表示梯度下降速率
eps 表示可允许误差
e 表示误差
T 表示初始温度
*/
int m = 11, n = 5;
double x[] = {-1, -0.8, -0.6, -0.4, -0.2, 0.0, 0.2, 0.4, 0.6, 0.8, 1.0};
double y[] = {-0.8669, -0.2997, 0.3430, 1.0072, 1.6416, 2.2022, 2.6558, 2.9823, 3.1755, 3.2416, 3.1974};
// double beta[] = {0.1, 0.1, 0.1, 0.1, 0.1};
double beta[] = {1.3, 2.2, 1.1, 0.9, 1.8};
double **J;
double *r;
double eps = 1e-5, e = 10, T = 1.0;
int step = 0;
int i, j;
srand((unsigned) time(NULL));
// J是一个m*n矩阵
J = (double **) malloc(sizeof(double *) * m);
for (i = 0; i < m; i++) {
J[i] = (double *) malloc(sizeof(double) * n);
}
r = (double *) malloc(m * sizeof(double));
while (e > eps) {
construct_J(m, beta, x, J);
construct_r(m, x, y, beta, r);
simulated_annealing(n, m, beta, T, x, y, J, r);
e = cal_error(m, beta, x, y);
step += 1;
T *= 0.999;
if (T < 1e-6) {
break;
}
}
free(J);
free(r);
}
由于新状态的随机性,当beta[] = {0.1, 0.1, 0.1, 0.1, 0.1}时,往往不能到达理想解
事实上,遗传算法也存在类似的问题,这里不再赘述
总结
对于前四种算法,其共同的缺点都是,在初始值不接近理想值的情况下,往往不能收敛到全局最优解, G a u s s – N e w t o n Gauss–Newton Gauss–Newton算法的优点是收敛速度快;而 L e v e n b e r g – M a r q u a r d t Levenberg–Marquardt Levenberg–Marquardt算法作为 G a u s s – N e w t o n Gauss–Newton Gauss–Newton算法的改进,牺牲了一些效率,但能在更大的范围内找到全局最优解; Q u a s i − N e w t o n Quasi-Newton Quasi−Newton方法(准 N e w t o n Newton Newton法/拟 N e w t o n Newton Newton法)最大的优势在于省去了矩阵求逆的过程,节省了计算量; N e l d e r – M e a d Nelder–Mead Nelder–Mead方法不同于前三种方法,不用求导就能进行拟合。
另外,关于以上算法的改进,Jean-Michel Renders 和 StCphane P. Flasse 提出了一种结合 Q u a s i − N e w t o n Quasi-Newton Quasi−Newton方法和遗传算法的算法[11]而 Jinshan Chen 提出了一种结合 N e l d e r – M e a d Nelder–Mead Nelder–Mead方法和遗传算法的算法[12],本文对这两者的工作不再进行复现。
参考文献
[1] Wikipedia contributors. (2022, October 18). Gauss–Newton algorithm. In Wikipedia, The Free Encyclopedia. Retrieved 14:02, November 15, 2022, from https://en.wikipedia.org/w/index.php?title=Gauss%E2%80%93Newton_algorithm&oldid=1116729836
[2] Wikipedia contributors. (2022, May 21). Levenberg–Marquardt algorithm. In Wikipedia, The Free Encyclopedia. Retrieved 14:03, November 15, 2022, from https://en.wikipedia.org/w/index.php?title=Levenberg%E2%80%93Marquardt_algorithm&oldid=1088958716
[3] Wikipedia contributors. (2022, August 21). Quasi-Newton method. In Wikipedia, The Free Encyclopedia. Retrieved 14:03, November 15, 2022, from https://en.wikipedia.org/w/index.php?title=Quasi-Newton_method&oldid=1105699584
[4] Wikipedia contributors. (2022, October 10). Broyden–Fletcher–Goldfarb–Shanno algorithm. In Wikipedia, The Free Encyclopedia. Retrieved 14:04, November 15, 2022, from https://en.wikipedia.org/w/index.php?title=Broyden%E2%80%93Fletcher%E2%80%93Goldfarb%E2%80%93Shanno_algorithm&oldid=1115153051
[5] Wikipedia contributors. (2022, June 29). Wolfe conditions. In Wikipedia, The Free Encyclopedia. Retrieved 14:05, November 15, 2022, from https://en.wikipedia.org/w/index.php?title=Wolfe_conditions&oldid=1095677130
[6] Wikipedia contributors. (2022, July 20). Line search. In Wikipedia, The Free Encyclopedia. Retrieved 11:30, November 19, 2022, from https://en.wikipedia.org/w/index.php?title=Line_search&oldid=1099362792
[7] Wikipedia contributors. (2022, October 5). Nelder–Mead method. In Wikipedia, The Free Encyclopedia. Retrieved 14:06, November 15, 2022, from https://en.wikipedia.org/w/index.php?title=Nelder%E2%80%93Mead_method&oldid=1114246182
[8] Saša Singer and John Nelder (2009) Nelder-Mead algorithm. Scholarpedia, 4(7):2928.
[9] 维基百科编者. 单纯形[G/OL]. 维基百科, 2021(20210903)[2021-09-03]. https://zh.wikipedia.org/w/index.php?title=%E5%8D%95%E7%BA%AF%E5%BD%A2&oldid=67497094.
[10] Wikipedia contributors. (2022, October 11). Simulated annealing. In Wikipedia, The Free Encyclopedia. Retrieved 14:08, November 15, 2022, from https://en.wikipedia.org/w/index.php?title=Simulated_annealing&oldid=1115450447
[11] Jean-Michel Renders and StCphane P. Flasse, “Hybrid Methods Using Genetic Algorithms for Global Optimization”. Belgium: Universitk Libre de Bruxelles, 1996.
[12] Jinshan Chen, “A New Hybrid Genetic Algorithm for Parameter Estimation of Nonlinear Regression Modeling”. Guangzhou: PLA Institute of Special Operation, 2015.