机器学习支持向量机SVM算法分类简析

支持向量机算法简介

支持向量机SVM是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。给定一组训练实例，每个训练实例被标记为属于两个类别中的一个或另一个，SVM训练算法创建一个将新的实例分配给两个类别之一的模型，使其成为非概率二元线性分类器。SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。
除了进行线性分类之外，SVM还可以使用所谓的核技巧有效地进行非线性分类，将其输入隐式映射到高维特征空间中。
支持向量机在高维或无限维空间中构造超平面或超平面集合，其可以用于分类、回归或其他任务。直观来说，分类边界距离最近的训练数据点越远越好，因为这样可以缩小分类器的泛化误差。

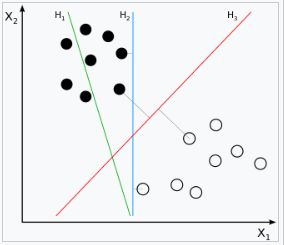
H1不能把类别分开，H2可以，但是只有很小的间隔，H3以最大的间隔将点分为两类。H2的泛化能力不好。两类别中离H3最近的点到H3的距离是一样远的。

支持向量机就是要找到一条线是让距离这条线最近的两类的点的距离相等还要使其尽可能的大。就是让上图的d尽可能的大。

超参数cc对SVM分类划分决策边界

首先准备数据，

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC 
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X [y<2,:2] #只取y<2的类别，也就是0 1 并且只取前两个特征
y = y [y<2] # 只取y<2的类别 # 分别画出类别0和1的点
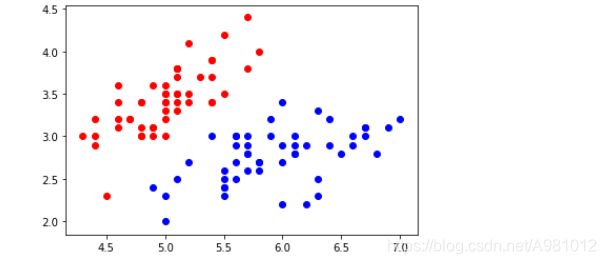
plt.scatter(X[y==0,0],X[y==0,1],color='red')
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()
# 标准化
standardScaler = StandardScaler()
standardScaler.fit(X)
#计算训练数据的均值和方差
X_standard = standardScaler.transform(X)
#再用scaler中的均值和方差来转换X，使X标准化
svc = LinearSVC(C=1e9)#线性SVM分类器
svc.fit(X_standard,y)# 训练svm

结果显示：

绘制出这两类的决策边界，此时cc=1e9

from matplotlib.colors import ListedColormap
def plot_decision_boundary(model,axis):
    x0,x1 = np.meshgrid(np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))
    X_new = np.c_[x0.ravel(),x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5, cmap=custom_cmap)# 绘制决策边界
plot_decision_boundary(svc,axis=[-3,3,-3,3])# x,y轴都在-3到3之间
# 绘制原始数据
plt.scatter(X_standard[y==0,0],X_standard[y==0,1],color='red')
plt.scatter(X_standard[y==1,0],X_standard[y==1,1],color='blue')
plt.show()

结果显示：

cc=0.01时的决策边界

svc2 = LinearSVC(C=0.01)
svc2.fit(X_standard,y)
plot_decision_boundary(svc2,axis=[-3,3,-3,3]) # x,y轴都在-3到3之间 # 绘制原始数据
plt.scatter(X_standard[y==0,0],X_standard[y==0,1],color='red')
plt.scatter(X_standard[y==1,0],X_standard[y==1,1],color='blue')
plt.show()

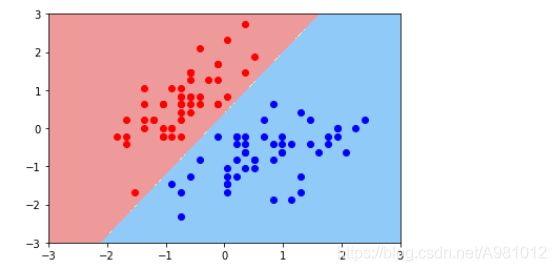
结果显示：

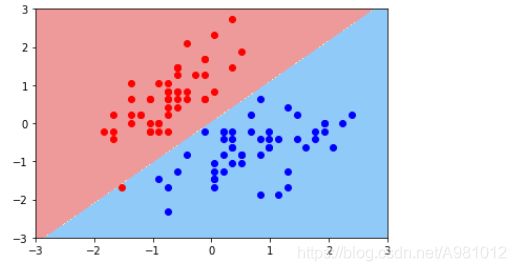
经过上面两个图的对比，可以明显看出决策边界划分的不同，第二个图中，有一个红点，被分到了蓝色区域。而代码中c是小于第一个图的代码中的c的，表明cc越小，容错的空间就越大。cc控制正则项的重要程度。
超参数相当于是在调整模型的复杂度

使用多项式特征进行划分

首先准备数据，以月亮数据为例，首先生成规范的月亮数据集

import numpy as np
import matplotlib.pyplot as plt 
from sklearn import datasets
X, y=datasets.make_moons()#使用生成的数据
print(X.shape)# (100,2)
print(y.shape)# (100,)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

结果显示：

生成带有噪声的月亮数据集

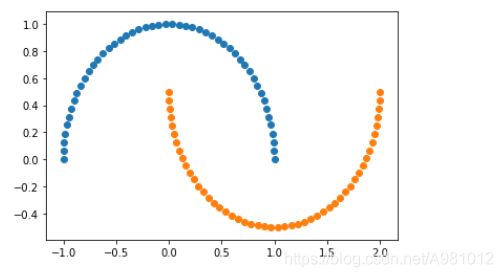
X,y=datasets.make_moons(noise=0.15,random_state=777)#随机生成噪声点，random_state是随机种子，noise是方差
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

结果显示：

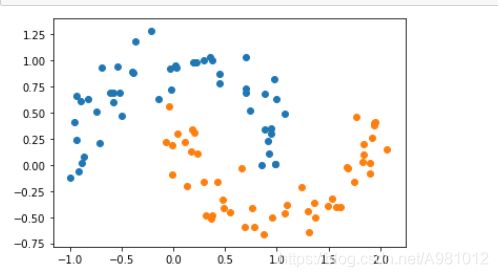
我们还可以使用核技巧来对数据进行处理，使其维度提升，使原本线性不可分的数据，在高维空间变成线性可分的。

from sklearn.svm import SVC
def PolynomialKernelSVC(degree,C=1.0):
    return Pipeline([
        ("std_scaler",StandardScaler()),
        ("kernelSVC",SVC(kernel="poly"))# poly代表多项式特征
    ])
poly_kernel_svc=PolynomialKernelSVC(degree=3)
poly_kernel_svc.fit(X,y)
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

结果显示：

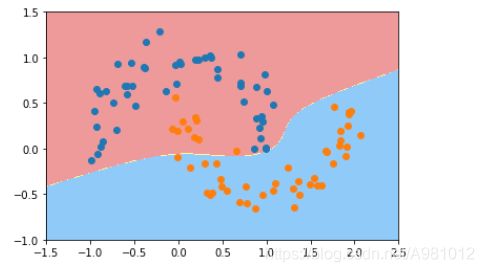
提取特征，归一化，然后将数据分类组织在一起，进行非线性分类

from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
def PolynomialSVC(degree,C=1.0):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),#生成多项式
        ("std_scaler",StandardScaler()),#标准化
        ("linearSVC",LinearSVC(C=C))#最后生成svm
    ])
poly_svc = PolynomialSVC(degree=3)
poly_svc.fit(X,y)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

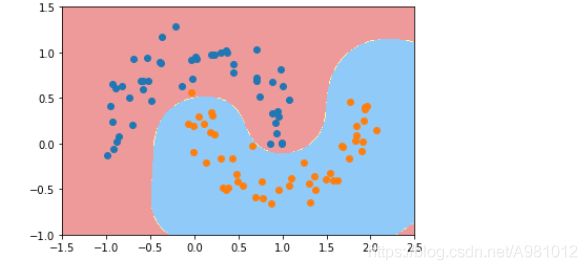
结果显示：

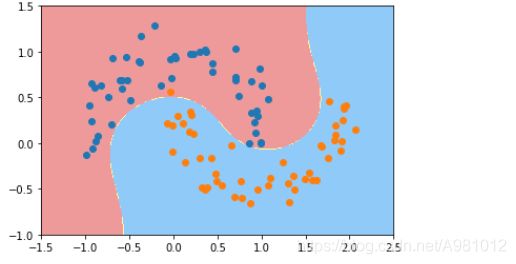
根据图像的直观显示，可以看出第二张图的非线性分类要好一些。

使用核函数进行划分

高斯核函数

高斯核函数的本质是将每个样本点映射到一个无穷多维度的特征空间中。核函数都是依靠升维使得原本线性不可分的数据变得线性可分。比如原本数据为x x的话，我们将数据转换为$ x^2 $$x^2$就可以将数据分开了。
首先生成线性不可分的数据

import numpy as np
import matplotlib.pyplot as plt 
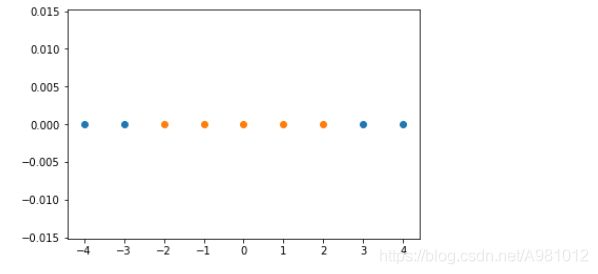
x = np.arange(-4,5,1)#生成测试数据
y = np.array((x >= -2 ) & (x <= 2),dtype='int')
plt.scatter(x[y==0],[0]*len(x[y==0]))# x取y=0的点, y取0，有多少个x，就有多少个y
plt.scatter(x[y==1],[0]*len(x[y==1]))
plt.show()

结果显示：

将线性不可分的数据利用高斯核函数升为二维的数据

# 高斯核函数 
def gaussian(x,l):
    gamma = 1.0
    return np.exp(-gamma*(x-l)**2)
l1,l2 = -1,1 
X_new = np.empty((len(x),2))
#len(x) ,2 
for i,data in enumerate(x):
    X_new[i,0] = gaussian(data,l1)
    X_new[i,1] = gaussian(data,l2)
plt.scatter(X_new[y==0,0],X_new[y==0,1])
plt.scatter(X_new[y==1,0],X_new[y==1,1])
plt.show()

显示为：

从这个图可以看出来，这两类数据点是可以使用线性分类分开的。

高斯函数 超参数$\gamma$的划分影响

首先准备数据集，以月亮数据集为例

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X,y = datasets.make_moons(noise=0.15,random_state=777)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

结果显示：

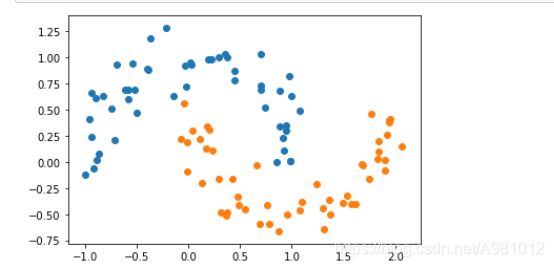
然后定义一个RBF核的支持向量机，设定$\gamma$的值为1，显示得到的决策边界

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC 
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])
svc=RBFKernelSVC()
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

结果显示：

$\gamma$=100时候的划分决策边界

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC 
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])
svc=RBFKernelSVC(100)
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

结果显示：

$\gamma$=10的时候划分的决策边界

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC 
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])
svc=RBFKernelSVC(10)
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

结果显示：

$\gamma$=0.1时的划分决策边界

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC 
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])
svc=RBFKernelSVC(0.1)
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

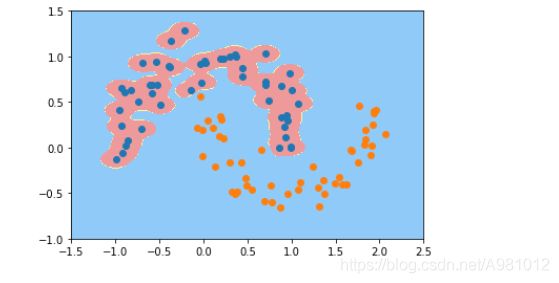
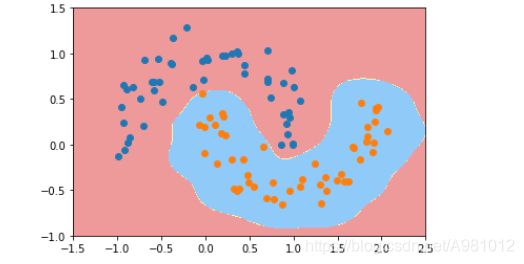
结果显示：

从上面的多个图的分析来看，$\gamma$取值越大，就越过拟合，对于分类是不好的，而$\gamma$取值过小的话，就会出现欠拟合，所以$\gamma$值相当于是在调整模型的复杂度。

SVM回归拟合度

与SVM分类相反，SVM回归是要让点在这个范围内的数量越多越好，越多表明回归的越好，我们可以使用SVM回归的拟合度来判断，SVM回归的程度好不好。

SVM回归就是让这些点尽可能多的在两条虚线之间，下面通过代码来显示拟合度来判断回归性能的好坏。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=777) # 把数据集拆分成训练数据和测试数据
from sklearn.svm import LinearSVR
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
def StandardLinearSVR(epsilon=0.1):
    return Pipeline([ ('std_scaler',StandardScaler()), ('linearSVR',LinearSVR(epsilon=epsilon)) ])
svr = StandardLinearSVR()
svr.fit(X_train,y_train)
svr.score(X_test,y_test) #0.6989278257702748

结果显示：

参考博客：
blog.sina.com.cn/s/blog_6c3438600102yn9x.html
.
如有错误请指正！