Chapter4 利用机器学习解决分类和回归问题

目录

4.1 机器学习和神经网络基本概念

4.1.1 感知器

4.1.2 前向传播

4.1.3 反向传播

4.1.4 过拟合和欠拟合

4.2 利用神经网络解决回归问题

4.2.1 问题介绍

4.2.2 利用pytorch解析数据

4.2.2 利用pytorch定义网络结构

4.2.3 开始训练

4.2.4 将模型进行保存

4.3 利用pytorch解决手写数字识别问题

---

4.1 机器学习和神经网络基本概念

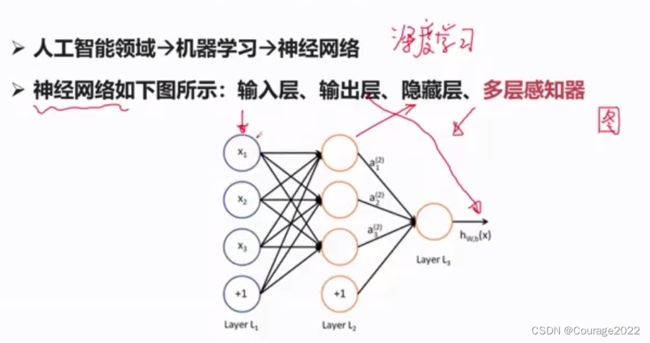
4.1.1 感知器

        每一个节点称之为一个神经元，神经元之间通过相应运算来完成信息的传递或者是特征的抽取。

        这个运算一般是指线性运算：，这里的b是指偏置项，这个我在机器学习的博客已经详细说明，这里不再解释。

        所谓深度学习，就是把中间的隐藏层变得更深。

         一个感知器可以理解为如上图的结构：如上上图从输入层到隐藏层有三个感知器，感知器的输入为上层的经过激活函数算出的结果，通过输入与权值的加权得到了加权和，再由非线性激活函数得到下一层的输入，总结以来，符合下列公式：。

4.1.2 前向传播

        前向传播的前提是参数已知，即全部已知（我们训练的参数）

4.1.3 反向传播

         我们定义损失为输出层真实值和测量值之间的偏差，通过反向传播实现参数的逐层调节参数（调节使得损失值最小），同时用梯度下降的方法进行求解，对参数方程进行求导拿到梯度，顺着导数下降的方向对导数进行调节直到找到最低点，最低点所对应的值就是我们所要求解的值。

4.1.4 过拟合和欠拟合

4.2 利用神经网络解决回归问题

4.2.1 问题介绍

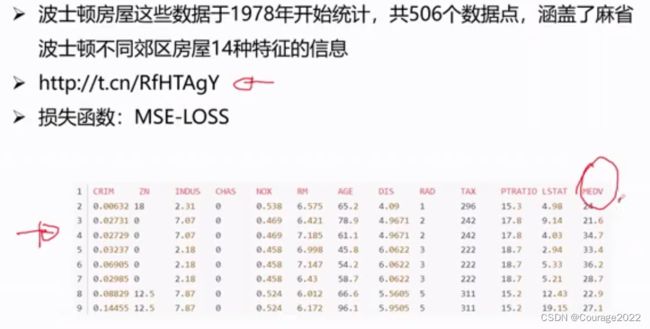
         利用pytorch回归网络解决房价模型预测问题：利用已知的十三种信息，预测第十四种信息！

4.2.2 利用pytorch解析数据

        我们要用回归问题解决房价预测问题，我们通过十三种的数据（地段、房屋面积、房价指数....）预测房价，数据集如下：

利用机器学习解决分类和回归问题

        我们首先要把数据集读取到我们的变量中，代码如下：

import torch
import numpy as np
import re
ff = open("/home/liuhongwei/桌面/housing.data").readlines()
data = []
for item in ff:
	out = re.sub(r"\s{2,}", " ",item).strip()           #由于不同列空的空格数量不一致，都处理为1个空格，即将多个空格编成一个空格
	print(out)
	data.append(out.split(" "))			    #空格对数据进行分割
data = np.array(data).astype(np.float)                      #转换成float类型
print(data)
print(data.shape)
Y = data[:,-1]
X = data[:,0:-1]                                            #定义自变量和因变量

X_train = X[0:496,...]
Y_train = Y[0:496,...]
X_test = X[496:,...]
Y_test = Y[496:,...]

print(X_train.shape)
print(Y_train.shape)
print(X_test.shape)
print(Y_test.shape)

        打开数据集文件，制定按行读取。对每一行进行读取，但存在一个问题，每一行的数据间隔虽然是以空格隔开的，但有的空了一个空格有的空了多个空格，我们用正则表达式去掉多余的空格。然后用np库函数将数据转换成浮点型向量。我们再定义了训练集和测试集。

4.2.2 利用pytorch定义网络结构

class Net(torch.nn.Module):
	def __init__(self,n_feature,n_out):
		super(Net,self).__init__()              		 #super来继承父类
		self.predict = torch.nn.Linear(n_feature,n_out)		#定义线性函数

	def forward(self,x):
		out = self.pridect(x)
		return out

net = Net(13,1)

        我们定义一个回归网络，初始化的时候传入特征（n_feature）和输出（n_out），用super继承父类，定义一个线性函数回归模型。定义了只有一个隐藏层的网络。

4.2.3 开始训练

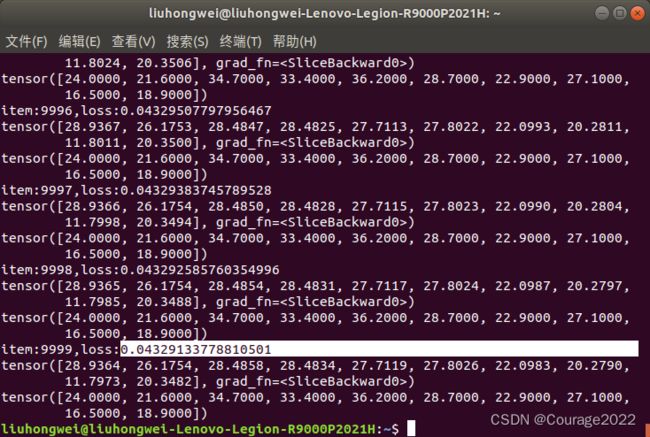
import torch
import numpy as np
import re


#解析数据

#读取所有行的数据
ff = open("/home/liuhongwei/桌面/housing.data").readlines()
data = []
for item in ff:
	out = re.sub(r"\s{2,}", " ",item).strip()           #由于不同列空的空格数量不一致，都处理为1个空格，即将多个空格编成一个空格
	#print(out)
	data.append(out.split(" "))			    #空格对数据进行分割
data = np.array(data).astype(np.float)                      #转换成float类型
#print(data)
#print(data.shape)
Y = data[:,-1]
X = data[:,0:-1]                                            #定义自变量和因变量

X_train = X[0:496,...]
Y_train = Y[0:496,...]
X_test = X[496:,...]
Y_test = Y[496:,...]

#print(X_train.shape)
#print(Y_train.shape)
#print(X_test.shape)
#print(Y_test.shape)

#搭建网络:搭建回归网络

class Net(torch.nn.Module):
	def __init__(self,n_feature,n_out):
		super(Net,self).__init__()              		 #super来继承父类
		self.predict = torch.nn.Linear(n_feature,n_out)		#定义线性函数

	def forward(self,x):
		out = self.predict(x)
		return out

net = Net(13,1)
#定义loss

loss_func = torch.nn.MSELoss()             				#采用均方损失作为loss


#定义优化器

optimizer = torch.optim.SGD(net.parameters(),lr = 0.0001)		#利用SGD作为损失函数，学习率=0.0001

#开始训练

for i in range(10000):
	x_data = torch.tensor(X_train,dtype = torch.float32)
	y_data = torch.tensor(Y_train,dtype = torch.float32)

	pred = net.forward(x_data)					#定义前向运算
	pred = torch.squeeze(pred)					#用线性函数计算出输出，这时的pred是二维的 496*1 496
	loss = loss_func(pred,y_data) * 0.001				#定义loss

	optimizer.zero_grad()						#将神经网络参数置为0
	loss.backward()							#反响传播
	optimizer.step()						#对优化好的参数进行更新
	
	print("item:{},loss:{}".format(i,loss))
	print(pred[0:10])						#预测结果的前十个值
	print(y_data[0:10])

        代码已经标注了，但是训练结果不尽人意。误差较大，即使加大训练次数也没用，因为已经收敛了，模型处于欠拟合的状态。我们修改损失函数Adam。

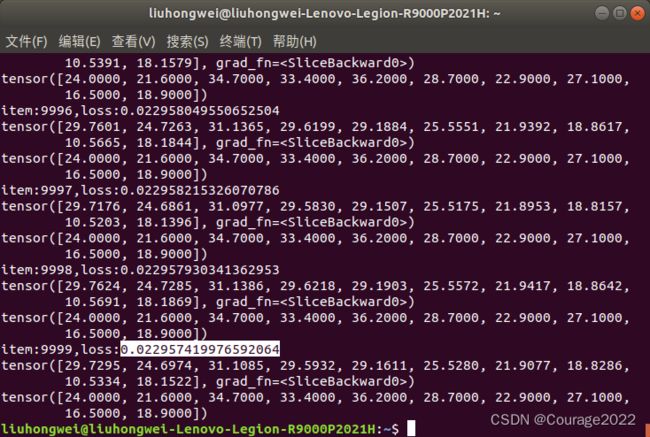
#optimizer = torch.optim.SGD(net.parameters(),lr = 0.0001)		#利用SGD作为损失函数，学习率=0.0001
optimizer = torch.optim.Adam(net.parameters(),lr = 0.0001)		#利用Adam作为损失函数，学习率=0.0001

        

         好像好一点了。我们再适当增加下学习率：

         好像又更好了一点。我们再加入隐藏层：

#搭建网络:搭建回归网络

class Net(torch.nn.Module):
	def __init__(self,n_feature,n_out):
		super(Net,self).__init__()              		 #super来继承父类
		self.hidden = torch.nn.Linear(n_feature,100)
		self.predict = torch.nn.Linear(100,n_out)		#定义线性函数

	def forward(self,x):
		out = self.hidden(x)
		out = torch.relu(out)
		out = self.predict(out)
		return out

net = Net(13,1)

        效果卓越！但是不难发现，测试集合和训练集合的loss存在差异性，主要是因为样本容量比较小

4.2.4 将模型进行保存

torch.save(net,"/home/liuhongwei/桌面/model.pkl")   #模型整体性保存

         在桌面上有了我们的模型数据，我们尝试去加载它。

import torch
import numpy as np
import re


class Net(torch.nn.Module):
	def __init__(self,n_feature,n_out):
		super(Net,self).__init__()              		 #super来继承父类
		self.hidden = torch.nn.Linear(n_feature,100)
		self.predict = torch.nn.Linear(100,n_out)		#定义线性函数

	def forward(self,x):
		out = self.hidden(x)
		out = torch.relu(out)
		out = self.predict(out)
		return out


#读取所有行的数据
ff = open("/home/liuhongwei/桌面/housing.data").readlines()
data = []
for item in ff:
	out = re.sub(r"\s{2,}", " ",item).strip()           #由于不同列空的空格数量不一致，都处理为1个空格，即将多个空格编成一个空格
	#print(out)
	data.append(out.split(" "))			    #空格对数据进行分割
data = np.array(data).astype(np.float)                      #转换成float类型
Y = data[:,-1]
X = data[:,0:-1]                                            #定义自变量和因变量

X_train = X[0:496,...]
Y_train = Y[0:496,...]
X_test = X[496:,...]
Y_test = Y[496:,...]


net = torch.load("/home/liuhongwei/桌面/model.pkl")
loss_func = torch.nn.MSELoss()             				#采用均方损失作为loss


x_test = torch.tensor(X_test,dtype = torch.float32)
y_test = torch.tensor(Y_test,dtype = torch.float32)

pred = net.forward(x_test)					#定义前向运算
pred = torch.squeeze(pred)					#用线性函数计算出输出，这时的pred是二维的 496*1 496
loss_test = loss_func(pred,y_test) * 0.001			#定义loss
print("loss_test:{}".format(loss_test))

4.3 利用pytorch解决手写数字识别问题

代码解释：

手写数字识别的数据集已经集成在torchvision这个包中，

import torchvision.datasets as dataset引用了数据集，我们用

train_data = dataset.MNIST(root = "/home/liuhongwei/桌面/dataset",train=True,transform=transforms.ToTensor(),download=True)

        加载了手写数字的训练集，定义了存放数据集的路径，下载训练集，并将训练集转化成tensor形式的，如果文件夹内没有该数据集则进行下载。

train_loader = data_untils.Dataloader(dataset = train_data,batch_size = 64,shuffle=True)

        对数据进行分批提取，分为64块进行读取并随机打乱。

        定义一个卷积层和一个线性层完成对手写数字的分类：在cnn的结构中，我们采用序列工具构建我们的网络结构，定义卷积层Conv2d（通道数量、输出的通道、卷积核大小）

import torch
import torchvision.datasets as dataset
import torchvision.transforms as transforms
import torch.utils.data as data_utils
from CNN import CNN
#data
train_data = dataset.MNIST(root="mnist",
                           train=True,
                           transform=transforms.ToTensor(),
                           download=True)

test_data = dataset.MNIST(root="mnist",
                           train=False,
                           transform=transforms.ToTensor(),
                           download=False)
#batchsize
train_loader = data_utils.DataLoader(dataset=train_data,
                                     batch_size=64,
                                     shuffle=True)

test_loader = data_utils.DataLoader(dataset=test_data,
                                     batch_size=64,
                                     shuffle=True)

cnn = CNN()
cnn = cnn.cuda()
#loss

loss_func = torch.nn.CrossEntropyLoss()

#optimizer

optimizer = torch.optim.Adam(cnn.parameters(), lr=0.01)

#training
for epoch in range(10):
    for i, (images, labels) in enumerate(train_loader):
        images = images.cuda()
        labels = labels.cuda()

        outputs = cnn(images)
        loss = loss_func(outputs, labels)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    print("epoch is {}, ite is "
          "{}/{}, loss is {}".format(epoch+1, i,
                                     len(train_data) // 64,
                                     loss.item()))
    #eval/test
    loss_test = 0
    accuracy = 0
    for i, (images, labels) in enumerate(test_loader):
        images = images.cuda()
        labels = labels.cuda()
        outputs = cnn(images)
        #[batchsize]
        #outputs = batchsize * cls_num
        loss_test += loss_func(outputs, labels)
        _, pred = outputs.max(1)
        accuracy += (pred == labels).sum().item()

    accuracy = accuracy / len(test_data)
    loss_test = loss_test / (len(test_data) // 64)

    print("epoch is {}, accuracy is {}, "
          "loss test is {}".format(epoch + 1,
                                   accuracy,
                                   loss_test.item()))

torch.save(cnn, "model/mnist_model.pkl")