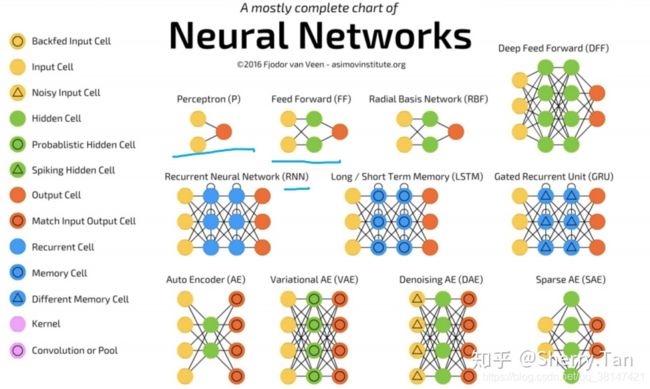
什么是多层感知机MLP(ANN)和反向传播?
多层感知机MLP(Multi Layer Perceptron )是一种特定的人工神经网络(Artificial Neural Networks)
在认识MLP之前,我们先回顾下前馈神经网络。
1、 前馈神经网络
前馈神经网络是最先发明也是最简单的人工神经网络 。它包含了安排在多个层中的多个神经元(节点)。相邻层的节点有连接或者边(edge)。所有的连接都配有权重。
下面是一个例子: 一个前馈神经网络可以包含三种节点:
一个前馈神经网络可以包含三种节点:
-
输入节点(Input Nodes):输入节点从外部世界提供信息,总称为「输入层」。在输入节点中,不进行任何的计算——仅向隐藏节点传递信息。
-
隐藏节点(Hidden Nodes):隐藏节点和外部世界没有直接联系(由此得名)。这些节点进行计算,并将信息从输入节点传递到输出节点。隐藏节点总称为「隐藏层」。尽管一个前馈神经网络只有一个输入层和一个输出层,但网络里可以没有也可以有多个隐藏层。
-
输出节点(Output Nodes):输出节点总称为「输出层」,负责计算,并从网络向外部世界传递信息。
在前馈网络中,信息只单向移动——从输入层开始前向移动,然后通过隐藏层(如果有的话),再到输出层。在网络中没有循环或回路 (前馈神经网络的这个属性和递归神经网络不同,后者的节点连接构成循环)。
下面是两个前馈神经网络的例子:
-
单层感知器——这是最简单的前馈神经网络,不包含任何隐藏层。
-
多层感知器——多层感知器有至少一个隐藏层。我们在下面会只讨论多层感知器,因为在现在的实际应用中,它们比单层感知器要更有用。
2、多层感知器
多层感知器(Multi Layer Perceptron,即 MLP)包括至少一个隐藏层(除了一个输入层和一个输出层以外)。单层感知器只能学习线性函数,而多层感知器也可以学习非线性函数。
下面是有一个隐藏层的多层感知机
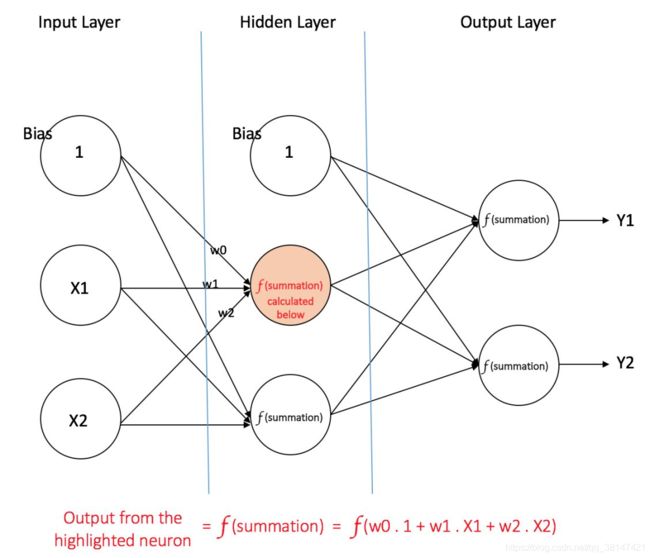
上图 表示了含有一个隐藏层的多层感知器。注意,所有的连接都有权重,但在图中只标记了三个权重(w0,,w1,w2)。
输入层:输入层有三个节点。偏置节点值为 1。其他两个节点从 X1 和 X2 取外部输入(皆为根据输入数据集取的数字值)。和上文讨论的一样,在输入层不进行任何计算,所以输入层节点的输出是 1、X1 和 X2 三个值被传入隐藏层。
隐藏层:隐藏层也有三个节点,偏置节点输出为 1。隐藏层其他两个节点的输出取决于输入层的输出(1,X1,X2)以及连接(边界)所附的权重。上图 显示了隐藏层(高亮)中一个输出的计算。其他隐藏节点的输出计算同理。需留意 f指代激活函数。这些输出被传入输出层的节点。
输出层:输出层有两个节点,从隐藏层接收输入,并执行类似高亮出的隐藏层的计算。这些作为计算结果的计算值(Y1 和 Y2)就是多层感知器的输出。
给出一系列特征 X = (x1, x2, …) 和目标 Y,一个多层感知器可以以分类或者回归为目的,学习到特征和目标之间的关系。
3、训练我们的多层感知器:反向传播算法
反向传播误差,通常缩写为「BackProp」,是几种训练人工神经网络的方法之一。这是一种监督学习方法,即通过标记的训练数据来学习(有监督者来引导学习)。
简单说来,BackProp 就像「从错误中学习」。监督者在人工神经网络犯错误时进行纠正。
一个人工神经网络包含多层的节点;输入层,中间隐藏层和输出层。相邻层节点的连接都有配有「权重」。学习的目的是为这些边缘分配正确的权重。通过输入向量,这些权重可以决定输出向量。
在监督学习中,训练集是已标注的。这意味着对于一些给定的输入,我们知道期望 / 期待的输出(标注)。
反向传播算法:最初,所有的边权重(edge weight)都是随机分配的。对于所有训练数据集中的输入,人工神经网络都被激活,并且观察其输出。这些输出会和我们已知的、期望的输出进行比较,误差会「传播」回上一层。该误差会被标注,权重也会被相应的「调整」。该流程重复,直到输出误差低于制定的标准。
上述算法结束后,我们就得到了一个学习过的人工神经网络,该网络被认为是可以接受「新」输入的。该人工神经网络可以说从几个样本(标注数据)和其错误(误差传播)中得到了学习。
4、通过一个例子来理解MLP
1、题目
假设我们有这样一个学生分数数据集:

两个输入栏表示了学生学习的时间和期中考试的分数。最终结果栏可以有两种值,1 或者 0,来表示学生是否通过的期末考试。例如,我们可以看到,如果学生学习了 35 个小时并在期中获得了 67 分,他 / 她就会通过期末考试。
现在我们假设我们想预测一个学习了 25 个小时并在期中考试中获得 70 分的学生是否能够通过期末考试。

这是一个二元分类问题,多层感知器可以从给定的样本(训练数据)进行学习,并且根据给出的新的数据点,进行准确的预测。在下面我们可以看到一个多层感知器如何学习这种关系。
2、MLP学习的具体过程
第一步 MLP的前向传播
MLP输入层有两个节点(除了偏置节点以外),两个节点分别接收「学习小时数」和「期中考试分数」。感知器也有一个包含两个节点的隐藏层(除了偏置节点以外)。输出层也有两个节点——上面一个节点输出「通过」的概率,下面一个节点输出「不通过」的概率。
在分类任务中,我们通常在感知器的输出层中使用 Softmax 函数作为激活函数,以保证输出的是概率并且相加等于 1。Softmax 函数接收一个随机实值的分数向量,转化成多个介于 0 和 1 之间、并且总和为 1 的多个向量值。所以,在这个例子中:
概率(Pass)+概率(Fail)=1
接下来看下图:

网络中所有的权重都是随机分配的。我们现在考虑图 5 中标注 V 的隐藏层节点。假设从输入连接到这些节点的权重分别为 w1、w2 和 w3(如图所示)。
神经网络会将第一个训练样本作为输入(我们已知在输入为 35 和 67 的情况下,通过的概率为 1)。
网络的输入=[35, 67]
期望的网络输出(目标)=[1, 0]
涉及到的节点的输出 V 可以按如下方式计算(f 是类似 Sigmoid 的激活函数):
V = f(1w1 + 35w2 + 67*w3)
同样,隐藏层的其他节点的输出也可以计算。隐藏层两个节点的输出,是输出层两个节点的输入。这让我们可以计算输出层两个输出的概率值。
假设输出层两个节点的输出概率分别为 0.4 和 0.6(因为权重随机,输出也会随机)。我们可以看到计算后的概率(0.4 和 0.6)距离期望概率非常远(1 和 0),所以上图中的网络被视为有「错误输出」。
第二步 反向传播和权重更新
我们计算输出节点的总误差,并将这些误差用反向传播算法传播回网络,以计算梯度。接下来,我们使用类似梯度下降之类的算法来「调整」网络中的所有权重,目的是减少输出层的误差。图 6 展示了这一过程(暂时忽略图中的数学等式)。
假设附给节点的新权重分别是 w4,w5 和 w6(在反向传播和权重调整之后)。
下图为多层感知机中的反向传播和更新步骤:
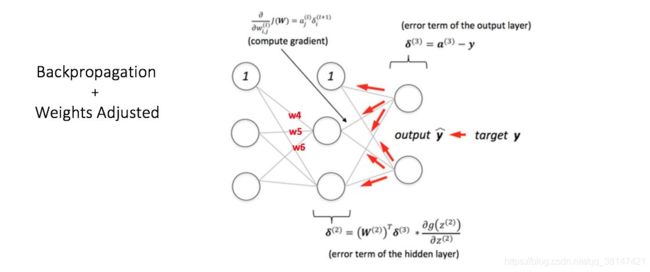
如果我们现在再次向网络输入同样的样本,网络应该比之前有更好的表现,因为为了最小化误差,已经调整了权重。如图 7 所示,和之前的 [0.6, -0.4] 相比,输出节点的误差已经减少到了 [0.2, -0.2]。这意味着我们的网络已经学习了如何正确对第一个训练样本进行分类。
在同样的输入下,多层感知器网络有更好的表现:

这里回避了数学公式和类似「梯度下降(Gradient Descent)」之类概念的解释,而是培养了一种对于算法的直觉。
最后说下MLP,全连接网络以及DNN的关系:
FullyConnected(FC)layer = 一层layer
MLP = 多层 FC layer构成的NN
DNN = MLP和CNN的集合相并,通常包括多个卷积layer和FC layer