E Parity Split （江西CCPC省赛）题解

前言：
solo了这场省赛，第三题开到此题，想了一小时，发现不会写，最后5题结束。
赛后补题感觉此题dp挺有意思的。

---

正文：
首先，我们可以很容易的确定此题为dp题，那么dp的本质无非是从前一个状态推现态。
我们通过数据范围可以发现此题解决此题的算法时间复杂度应该是O(n^2)。
不难分析出，我们可以将所给出的字符串转化为01串，再通过前缀异或和，以O(1)时间得到任意区间内的奇偶情况。

现在应该思考，我们的状态转移方程是什么？

通过以往的经验，此题应该是用长度为i-1的字符串答案推长度为i的字符串答案。然而实际上，此题不是。（太菜了）

任何动态规划问题都要从最简单的情况开始。

假设01串为s，pre[i] = s[0] ^ s[1] ^ ... ^ s[i] 即前缀异或和。

如果只分一个部分，那么s一定是一个答案。

现在我们将s分割成两部分，第一部分为s[0]s[1]s[2]...s[i] ，第二部分为s[i + 1]s[i + 2] ... s[n - 1]。可以得到一个推论，如果pre[n - 1] == 0，那么此处的i就可以作为一个解。

现在我们将s分割成三部分，第一部分为s[0]s[1]...s[l - 1] , 第二部分为s[l]s[l + 1]...s[r] ，第三部分为s[r + 1]s[r + 2]...s[n - 1]。可以得到一个推论， 如果pre[r] ^ pre[l - 1] == pre[n - 1] , 那么这对(l,r)为一个答案。

但是，题目是可以分成若干部分的，我们该如何从这三个简单的结论，推到整体上呢？

假设存在一个解(l,r),满足不存在(L,R) , (0<=L 为一组解。那么我们的答案就可以用s[l]s[l + 1] ... s[r] 中的解更新。

假设从在两个解(l1 , r1) , (l2 , r2) ,如图所示：

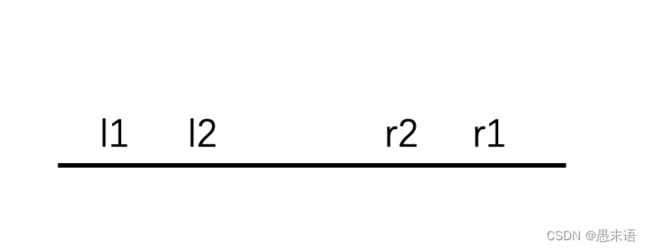
同样保证不存在(L,R) , (l1 < L< l2) & (r2 < R < r1) 为一组解。那么我们的答案就可以用s[l2]s[l2 + 1]...s[r2] 中的解更新。

现在假设我们得到一组(l,r)，pre[r] ^ pre[l - 1] = p (p = 1 or p = 0) ， 那么假设以这组（l,r）为中心，其对答案的贡献应该为number ， number 为满足（L，R），（L <= l） & (R >= r) & pre[R] ^ pre[L - 1] = p & (L, R)为一组解 的个数。

所以，我们的状态转移方程应该是从（L，R） 转移到（l,r）其中满足l<=L && r >= R 。

---

AC代码：

#include
using namespace std;
#define ll long long
const int mod = 998244353;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    string s;
    cin>>s;
    int n = s.length();
    vector<int>a(n) , pre(n);
    for(int i = 0; i < n; i ++){
        a[i] = (s[i] - '0') % 2 ;
        pre[i] = (i == 0 ? 0 : pre[i - 1]) ^ a[i];
    }
    auto get = [&](int l , int r){
        if(r < 0)return 0;
        return pre[r] ^ (l == 0 ? 0 : pre[l - 1]);
    };
    vector<vector<ll>>suf(n + 1 , vector<ll>(2));
    
    vector<vector<ll>>d(n + 1,  vector<ll>(2));
    ll ans = 0 ;
    for(int i = 0 ;i < n ; i ++){ 
        for(int j = 0 ; j < n; j++)d[j][0] = d[j][1] = 0;

        for(int j = n - 1; j >= i - 1 ;j --){
            ll res = 0;
            res += suf[j + 1][get(i , j)];
            res %= mod;
            if(i == 0 && j == n - 1)res = 1;
            d[0][get(i , j)] += res;
            d[0][get(i , j)] %= mod;
            d[j + 1][get(i , j)] -= res;
            d[j + 1][get(i , j)] += mod;
            d[j + 1][get(i , j)] %= mod;
            
            
            ans += res;
            ans %= mod;
        }
        for(int j = 0 ; j < n ; j ++){      
            d[j][0] += (j == 0 ? 0 : d[j - 1][0]) ;
            d[j][0] %= mod;
            d[j][1] += (j == 0 ? 0 : d[j - 1][1]) ;
            d[j][1] %= mod;
            suf[j][0] += d[j][0];
            suf[j][0] %= mod;
            suf[j][1] += d[j][1];
            suf[j][1] %= mod;

        }
        
    }
    cout<<ans<<'\n';
    
    return 0 ;
}