leetcode
文章目录
- 排序
-
- 215.数组中的第K个最大元素
- 347.前k个高频元素
- 435.无重叠区间
- 分治
-
- 剑指offer 07.重建二叉树
- 932.漂亮数组
- 回溯
-
- 46.全排列
- 47.全排列Ⅱ
- 37.解数独
排序
215.数组中的第K个最大元素
快速排序(分治):
针对一个区间,以区间内的第一个数字为基准数,然后设置两个指针,一个从前往后寻找第一个比基准数大的数字,一个从后往前寻找第一个比基准数小的数字,然后交换两个数字,直到指针指向同一个数字结束,并将基准数与该数交换位置。
这样得到的序列,左边都比基准数小,右边都比基准数大。然后将该序列拆分为左右两个序列进行同样的操作。
void quicksort(vector<int>& num,int l,int r){
if(l>r)return;
int i=l,j=r,t;
while (i!=j){
//升序
while(num[j]>=num[l]&&i<j)j--;
while(num[i]<=num[l]&&i<j)i++;
if(i<j){
t=num[i];
num[i]=num[j];
num[j]=t;
}
}
t=num[i];
num[i]=num[l];
num[l]=t;
quicksort(num,l,i-1);
quicksort(num,i+1,r);
}
347.前k个高频元素
遍历一次数组,用map记录出现的数字及该数字出现的次数,然后将其以pair的形式放进优先队列中,并以次数降序排序。然后不断弹出队列元素,直到剩下k个元素。
优先队列自定义比较函数的写法:
//struct重定义
struct cmp{
bool operator()(pair<int,int>&a,pair<int,int>&b){
return a.second>b.second;
}
};
priority_queue<pair<int,int>,vector<pair<int,int>>,cmp>q;
//比较函数重定义
//作为类成员函数,必须声明static
static bool cmp(pair<int,int>&a,pair<int,int>&b){
return a.second>b.second;
}
//引用写法
priority_queue<pair<int,int>,vector<pair<int,int>>,decltype(&cmp)>q(cmp);
435.无重叠区间
该题为贪心,但是我主要卡在了自定义排序。
第一种写法(会超时):
static bool cmp(vector<int>a,vector<int>b){
if(a[0]==b[0])return a[1]<b[1];
return a[0]<b[0];
}
//函数引用
sort(intervals.begin(),intervals.end(),cmp);
第二种写法(能过):
//lambda表达式写法
sort(intervals.begin(), intervals.end(), [&](vector<int>& a, vector<int>& b) {
if(a[0]==b[0])return a[1]<b[1];
return a[0]<b[0];
});
分治
剑指offer 07.重建二叉树
思路很简单,前序遍历中第一个即为当前的根节点,然后中序遍历数列中的根节点左侧为左子树,根节点右侧为右子树。然后递归地重建左子树和右子树即可。
主要是注意一些细节:
一是注意NULL和nullptr地区别,NULL只是一个宏定义,而nullptr是一个空指针,所以在递归结束地时候返回的应该是nullptr。
二是要注意每次递归时两个数组左边界和右边界。
三是可以用map记录中序遍历中节点值对应的下标,减少每次搜索的时间。
/**
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
map<int,int>mp;
TreeNode* rebulid(vector<int>& preorder,vector<int>&inorder,int pre_l,int pre_r,int in_l,int in_r){
if(pre_l>pre_r) return nullptr;
TreeNode* t=new TreeNode(preorder[pre_l]);
if(pre_l==pre_r) return t;
int i=mp[t->val];
int k=i-1-in_l; //左子树长度
t->left=rebulid(preorder,inorder,pre_l+1,pre_l+1+k,in_l,i-1);
t->right=rebulid(preorder,inorder,pre_l+2+k,pre_r,i+1,in_r);
return t;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
for(int i=0;i<inorder.size();i++){
mp[inorder[i]]=i;
}
return rebulid(preorder,inorder,0,inorder.size()-1,0,inorder.size()-1);
}
};
932.漂亮数组
漂亮数组指对于每个 i < j,都不存在 k 满足 i < k < j 使得 A[k] * 2 = A[i] + A[j]。
①一开始只有一个思路,那就是左边全是奇数,右边全是偶数,如果左边和右边内部分别满足漂亮数组,那么左边+右边的数组也一定是漂亮数组,因为偶数加奇数一定为奇数。
②然后还有一个性质,那就是
如果 2∗Y ≠ X+Z,则 2∗(k∗Y+b)≠k∗X+b+k∗Z+b 一定成立
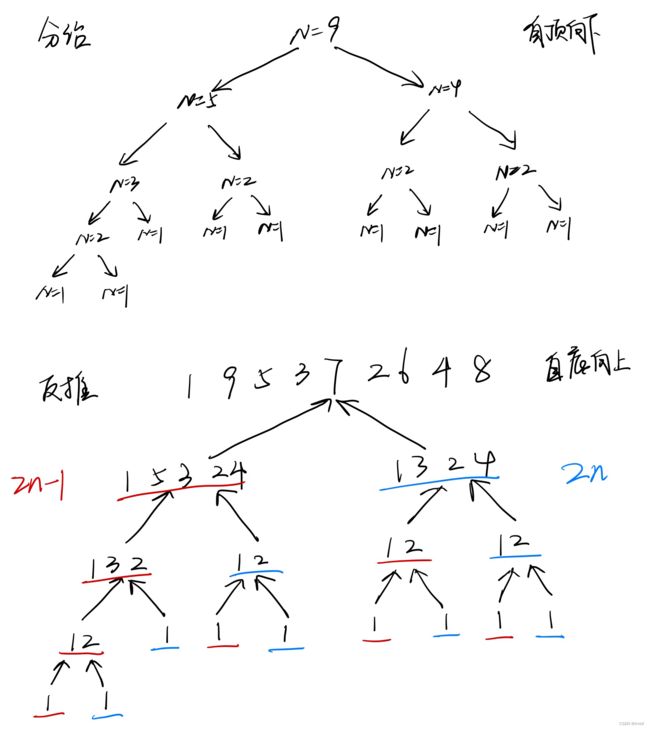
所以,结合①和②,可以采用自顶向下的分治的方法。
针对给定的N,将其等分为两部分,前半部分为长度为(N+1)/2的奇数数组,后半部分为长度为N/2的偶数数组。然后两部分进行分治。
分别得到两个数组后,再根据性质②,利用2n-1和2n分别将数值转换成N以内的奇数和偶数。
class Solution {
public:
vector<int> f(int n){
if(n==1) return vector<int>{1};
vector<int>l=f((n+1)/2);
vector<int>r=f(n/2);
vector<int>ans;
for(auto i:l) ans.push_back(i*2-1);
for(auto i:r) ans.push_back(i*2);
return ans;
}
vector<int> beautifulArray(int n) {
return f(n);
}
};
回溯
46.全排列
把这个题看成:在长度为n的数组中填入给定的nums中的数,看有多少种情况。
从左往右依次遍历,记录每次遍历完成的个数cnt,
当cnt=数组个数的时候,将当前的排列加入ans数组中。
cnt<数组个数的时候,继续尝试填下一个位置,下标为cnt的左边都是已经填好的位置,右边都是还未填入的位置,回溯的时候动态维护这个数组即可。这样可以省去标记数组。
class Solution {
public:
void backtrack(vector<vector<int>>& ans,vector<int>& nums,int cnt){
int len=nums.size();
if(cnt==len){
ans.push_back(nums);
return ;
}
for(int i=cnt;i<len;i++){
swap(nums[i],nums[cnt]);
backtrack(ans,nums,cnt+1);
swap(nums[i],nums[cnt]);
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>>ans;
backtrack(ans,nums,0);
return ans;
}
};
47.全排列Ⅱ
去重一定要排序,方便通过相邻的节点来判断是否使用过
而在本题解中,我们选择对原数组排序,保证相同的数字都相邻,然后每次填入的数一定是这个数所在重复数集合中「从左往右第一个未被填过的数字」,即如下的判断条件:
只要保证,在填第cnt个数的时候重复数字只会被填入一次。
class Solution {
public:
int vis[10];
void backtrack(vector<vector<int>>& ans,vector<int>& nums,vector<int>& per,int cnt){
int len=nums.size();
if(cnt==len){
ans.push_back(per);
return ;
}
for(int i=0;i<len;i++){
if(vis[i]||i>0&&nums[i]==nums[i-1]&&!vis[i-1])continue;
vis[i]=1;
per.push_back(nums[i]);
backtrack(ans,nums,per,cnt+1);
per.pop_back();
vis[i]=0;
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<vector<int>>ans;
sort(nums.begin(),nums.end());
vector<int>per;
backtrack(ans,nums,per,0);
return ans;
}
};
37.解数独
思路1:回溯
- 用三个数组分别标记每行、每列、每个3x3宫格内是否出现过数字1-9,初始化为0,注意3x3宫格数组的定义方法。
- 用一个pair数组记录空白位置的坐标 i 和 j 。
- 遍历一遍初始board,更新以上的四个数组。
- 算法过程:当前遍历到第 k 个空白的位置坐标,针对该位置,依次尝试数字1-9是否可以填入,如果可以,将board中该位置置为当前数字,进入下一次递归。当递归到填好最后一个空白的位置,仍没有冲突,则找到答案,进行回溯。
class Solution {
public:
bool flag=0;
int row[10][10]={0};
int column[10][10]={0};
int block[4][4][10]={0};
vector<pair<int,int>>blank;
void backtrack(vector<vector<char>>& board,int k){
if(blank.size()==k){
flag=1;
return;
}
auto [i,j]=blank[k];
for(int d=1;d<=9;d++){
if(!flag&&!row[i][d]&&!column[j][d]&&!block[i/3][j/3][d]){
board[i][j]='0'+d;
row[i][d]=column[j][d]=block[i/3][j/3][d]=1;
backtrack(board,k+1);
row[i][d]=column[j][d]=block[i/3][j/3][d]=0;
}
}
}
void solveSudoku(vector<vector<char>>& board) {
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(board[i][j]=='.'){
blank.emplace_back(i,j);
}
else{
int digit=board[i][j]-'0';
row[i][digit]=column[j][digit]=block[i/3][j/3][digit]=1;
}
}
}
backtrack(board,0);
}
};
思路2:位运算优化
借助位运算,可以优化思路1的方法。
- 数字 d 的二进制表示的第 i 位为1,表示数字 i + 1 已经出现过。
例digit = 0101 1000,表示数字4、5、7已经出现过了。 - 对于位置[i , j]的数字
若cow[i]、column[j]、block[i/3][j/3]中第k位为1,则表示该位置不能填入数字k+1。
对cow[i]、column[j]、block[i/3][j/3]的值按位取反后,若第k位为1,则表示该位置可以填入数字k+1。
所以,通过寻找1的位置k来确认该k+1是否可以填入该位置。
因为,按位取反后,数字的高位也会全部变成1,所以需要将该数和(1 1111 1111)2=(1FF)16进行按位与运算&,将无关的位置置为0。 - 进行d&(-d)运算可以得到d的二进制表示中的最低位的1。
-d是以补码的形式存储,-d=~d+1。 - 利用函数__builtin_ctz()
这个函数的作用是返回输入数的二进制表示从最低位开始的连续的0的个数。 - 遍历完当前位后,可以用d和最低位的1进行按位异或运算,就可以将最低位的1从b中去掉,然后枚举下一个1。
class Solution {
public:
bool flag=0;
int row[9]={0};
int column[9]={0};
int block[3][3]={0};
vector<pair<int,int>>blank;
void flip(int i,int j,int digit) {
row[i]^=(1<<digit);
column[j]^=(1<<digit);
block[i/3][j/3]^=(1<<digit);
}
void backtrack(vector<vector<char>>& board,int k){
if(blank.size()==k){
flag=1;
return;
}
auto [i,j]=blank[k];
int mask=~(row[i]|column[j]|block[i/3][j/3])&0x1ff;
for (;mask&&!flag;mask&=(mask-1)) {
int digitMask=mask&(-mask);
int digit=__builtin_ctz(digitMask);
flip(i,j,digit);
board[i][j] = digit+'0'+1;
backtrack(board,k+1);
flip(i,j,digit);
}
}
void solveSudoku(vector<vector<char>>& board) {
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(board[i][j]=='.'){
blank.emplace_back(i,j);
}
else{
flip(i,j,board[i][j]-'0'-1);
}
}
}
backtrack(board,0);
}
};