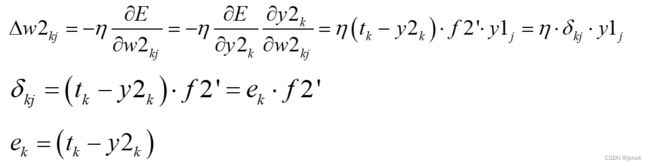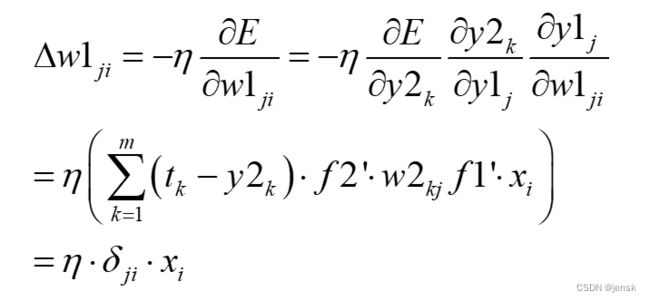基于BP神经网络的手写数字识别
本文参考到的博客会在正文贴出来,如有问题请联系我
数据集和代码已上传到github,有需者自取
https://github.com/jenskb/matlab.git
1 理论部分
1.1 BP算法的流程图
图1 BP算法的流程图
简单解释一下,BP算法的训练过程就是先取一个样本进行正向传播,然后得到一个输出,这个输出要和目标值相减,得到的就是误差值,为了将这个误差值减小,我们就必须重新调整权值和阈值,以满足我们的要求,调整完后就进行下一次样本的训练,直至样本用尽, 这是计算平均误差,判断是否满足我们的精度要求,或者判断迭代次数是否达到我们设定的上限,其中任何一个条件满足即可结束训练,不然的话就再进行一个全部样本的训练。
1.2 前向传播
输出层第k个神经元的输出为:
定义误差函数为:
以上就是正向传播的三个公式 ,应该说比较简单
不过我还是简单解释一下,神经元的输出=激活函数(每个输入乘以相对应的权值之和+阈值)
为什么权值乘以输入之和,因为隐层或输出层的任意一个神经元都有许多个输入,自然就需要用一个求和符号将所有值相加起来
误差函数就是求均方差:就是每个预期输出减去神经网络的输出的平方和/2
1.3 误差反向传播过程
反向传播过程的BP神经网络的灵魂,通过这个过程调整权值和阈值使误差函数值降到最低。
但为什么能降到最低的原因就是用到了梯度下降法,举个例子,可能比较好理解这个方法的思想:
瞎子下山法,瞎子站在山顶,如果他想以最快的速度下山,那么他势必要找到最陡的坡下山,而梯
度就是最陡的方向。
以下回到正题:
图3 误差反向传播的流程图
隐含层 j 节点到输出层的 k 节点权值变化:
同理可得阈值变化
输入层 i 节点到隐含层 j 节点的权值变化:
其中:
•同理可得隐含层的偏置变化:
以上需要注意的几个点:
1、误差函数对w2kj求偏导只涉及到隐含层的 j 点到输出层的 k 点这两个点之间的权值,和隐含层到输出层的其他权值无关,所以求偏导后没有累加符号。
2、而误差函数对w1ji求偏导,则涉及到隐含层到输出层的所有权值,因为w2kj(这里表示所有权值),每一个都包含了一个w1ji(这里指只是输入层到隐含层的某一个权值),所以就需要把每个偏导都加起来。
如果自己推不出来可以参考下面这个博客
BP 神经网络算法原理_懒惰的gler的博客-CSDN博客_bp神经网络原理本篇文章主要根据《神经网络与机器学习》和《人工神经网络原理》两本书,对 BP 神经网络的数学推导过程做了一个总结,为自己进入深度学习打下一个基础。https://blog.csdn.net/u010858605/article/details/69857957
2 实践部分
实践部分参考的是这篇博客
MATLAB--基于BP神经网络的手写数字识别_向着怪阿姨拔足狂奔的博客-CSDN博客_基于bp神经网络的手写数字识别
2.1 获取数据并处理
既然要识别数字我们必须要有样本,可以从网上搜Minist手写数据库,当然还需要一定的操作才能把样本读取处理。总共5000张,其中每个数字500张,大小是28*28。
将数据下载下来后和代码放在同一个文件夹下,方便读取。
root='./data';
out_Files = dir(root);dir函数的功能:是将路径下的目录名或文件名读取出来并返回一个结构体。
于是我们就得到第一层目录名
接着获取第一层目录下的文件名:
rootpath=strcat(root,'/',out_Files(i).name);
in_filelist=dir(rootpath);接着是根据相对路径名,使用imread函数将所有图片读取到一个矩阵里。
tempind=tempind+1;
img{tempind}=imread(strcat(rootpath,'/',in_filelist(j).name));效果图如下
2.2 粗网格特征提取法
简单画了个流程图
图4 粗网格特征提取法流程图
for i=1:length(img)
bw2=im2bw(img{i},graythresh(img{i}));
bw_7050=imresize(bw2,[50,50]);
for cnt=1:5
for cnt2=1:5
Atemp=sum(bw_7050(((cnt*10-9):(cnt*10)),((cnt2*10-9):(cnt2*10))));
lett((cnt-1)*5+cnt2)=sum(Atemp);
end
end
lett=((100-lett)/100);
lett=lett';
img_feature(:,i)=lett;
end将刚才读取到的图片每一张都进行2值化(im2bw),然后调整为50*50的大小(imresize),接着按10*10一个网格将所有黑色的个数相加起来,最后得到一个一个1*25的特征行向量,100-lett/100是将算出白色占比,lett'是转置为列向量,最后将5000列都存放在img_feature中。
2.3 贴标签
class=10;
numberpclass=500;
ann_label=zeros(class,numberpclass*class);
ann_data=img_feature;
for i=1:class
for j=numberpclass*(i-1)+1:numberpclass*i
ann_label(i,j)=1;
end
end 第1个500张标1,第2个500张标2,以此类推,下图显示的是每500张的第一张的标签图
2.4 选择数据进行训练和测试
选取4500张图为训练集,500张为测试集
k=rand(1,numberpclass*class); %生成1行5000列的一个随机矩阵
[m,n]=sort(k); %m是已经排序后的k,n是其索引,也就是k(n)=m
ntraindata=4500;
ntestdata=500;
train_data=ann_data(:,n(1:ntraindata));
test_data=ann_data(:,n(ntraindata+1:numberpclass*class));
train_label=ann_label(:,n(1:ntraindata));
test_label=ann_label(:,n(ntraindata+1:numberpclass*class));
%% BP神经网络创建,训练和测试
layer=30;%隐含层个数
net=newff(train_data,train_label,layer);%创建网络
net.trainParam.lr=0.2;%学习率
net.trainFcn='trainrp';%训练方法
net.trainParam.epochs=1000;%迭代次数
net.trainParam.goal=0.001;%误差参数
% 网络训练
net=train(net,train_data,train_label);newff是创建神经网络的函数,这里的参数有输入数据train_data,输入的目标数据train_label,和隐含层神经个数layer
trainrp是弹性梯度下降法
2.5 仿真测试
an=sim(net,test_data);
for i=1:length(test_data)
out(i)=find(an(:,i)==max(an(:,i)));
end
predict_label=out;
%% 正确率计算
[u,v]=find(test_label==1);
label=u';
error=label-predict_label;
accuracy=size(find(error==0),2)/size(label,2);
%取测试集和预测集以及误差集的前20个,做一个简单的比较
comparable(1,:)=u(1:20)'-1;
comparable(2,:)=predict_label(1,[1:20])-1;
comparable(3,:)=error(1,[1:20]); 例如第一列是0.4388最大,那么它所在的位置4就是它的标签
最后我分别取测试集、预测集和错误集的前20个做一个直观的比较,显然3和8以及7和9容易判断错
sim函数是仿真函数
find函数就是找目标的位置
准确率在82%左右
以上对神经网络的训练和测试都是用到工具箱的函数,如果有兴趣研究的同学可以考虑自己用代码把这部分复现一下。