基于BP神经网络的含水率预测模型matlab仿真

欢迎订阅《FPGA学习入门100例教程》、《MATLAB学习入门100例教程》

目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

       在人工神经网络的发展历史上，感知机(Multilayer Perceptron，MLP)网络曾对人工神经网络的发展发挥了极大的作用，也被认为是一种真正能够使用的人工神经网络模型，它的出现曾掀起了人们研究人工神经元网络的热潮。单层感知网络（M-P模型）做为最初的神经网络，具有模型清晰、结构简单、计算量小等优点。但是，随着研究工作的深入，人们发现它还存在不足，例如无法处理非线性问题，即使计算单元的作用函数不用阀函数而用其他较复杂的非线性函数，仍然只能解决线性可分问题．不能实现某些基本功能，从而限制了它的应用。增强网络的分类和识别能力、解决非线性问题的唯一途径是采用多层前馈网络，即在输入层和输出层之间加上隐含层。构成多层前馈感知器网络。
      20世纪80年代中期，David Runelhart。Geoffrey Hinton和Ronald W-llians、DavidParker等人分别独立发现了误差反向传播算法(Error Back Propagation Training)，简称BP，系统解决了多层神经网络隐含层连接权学习问题，并在数学上给出了完整推导。人们把采用这种算法进行误差校正的多层前馈网络称为BP网。
BP神经网络具有任意复杂的模式分类能力和优良的多维函数映射能力，解决了简单感知器不能解决的异或(Exclusive OR，XOR)和一些其他问题。从结构上讲，BP网络具有输入层、隐藏层和输出层；从本质上讲，BP算法就是以网络误差平方为目标函数、采用梯度下降法来计算目标函数的最小值。

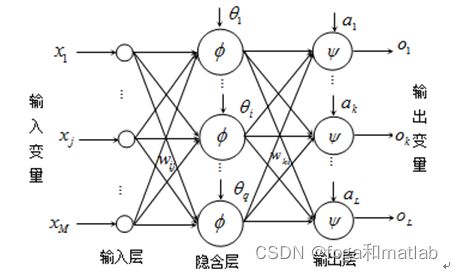
      BP神经网络，即Back Propagation神经网络，其本质是一种基于误差反馈传播的神经网络算法。从结构上讲，BP神经网络是由一个信息的正向传播网络和一个误差的反向传播网络两个模块构成。BP神经网络的基本结构如下图所示：

       从图2的结构可知，BP神经网络主要由输入层，隐含层以及输出层构成。来自外界的信息通过输入层传输进入到隐含层进行处理，并由输出层输出处理结果。当BP神经网络的输出结果和其期望结果之间的误差较大的时候，则进入反向传播阶段，并进行进行审计网络权值的修正，直到输出结果和期望结果误差满足一定条件为止。

 

 

 BP神经网络模型包括其输入输出模型、作用函数模型、误差计算模型和自学习模型。

二、核心程序

clc;
clear;
close all;
warning off;
rand('state',0);

%%
%输入数据为温度T，风速V，厚度h以及时间t
Ni         = 4;
No         = 1;
Num_Hidden = 8;%隐含层数量
%输出为水分比FSB
Num        = Ni + No;
%%
%训练数据设置
data = xlsread('datas\data.xlsx'); 
[R,C] = size(data);
for i = 1:C/Num
    tmps = [];
    tmps = data(:,Num*(i-1)+1:Num*(i));
    tmps_check = tmps(:,1);
    tmps(isnan(tmps_check),:)=[];
    Train_input1{i}  = tmps(:,1:Ni);
    Train_output1{i} = tmps(:,Ni+1:Ni+No);
end

 

%%
%输入BP神经网络进行训练
P = [];
T = [];
for i=1:length(Train_input1);
    P = [P;Train_input1{i}];
    T = [T;Train_output1{i}];
end
 

%BP神经网络参数
net = newff(P',T',Num_Hidden);
net.adaptFcn='adaptwb';  
net.trainParam.mu=1.0000e-05;  
net.trainParam.mu_dec=0.1000;  
net.trainParam.mu_inc=10;  
net.trainParam.mu_max=1e10;  
net.trainparam.mc=0.2;                                                                                                                       
net.trainparam.lr=0.005; 
net.trainparam.epochs=2000; 
net.trainparam.goal=1e-9; 
% net.trainParam.max_fail=6;  
% net.trainParam.min_grad=1e-7;  
% net.performFcn='mse';  
net.trainFcn       ='trainlm';
net = train(net,P',T');   

save model.mat net
%输出BP神经网络的参数
Input_W        = net.IW{1,1}  
LayerOne_Bias  = net.b{1}
LayerOneToTwo_W= net.LW{2,1} 
LayerTwo_Bias  = net.b{2}  
%%
%通过BP神经网络训练后测试
for i = 1:length(Train_input1);
    y1{i} = sim(net,Train_input1{i}');
end
 
%%
%各种指标的输出分析
NAME{1} = ['T=55,v=0.3,h=3']; 
NAME{2} = ['T=55,v=0.6,h=3'];
NAME{3} = ['T=55,v=0.7,h=3'];
NAME{4} = ['T=55,v=1.2,h=3'];
NAME{5} = ['h=3,T=55,v=0.9'];  
NAME{6} = ['h=6,T=55,v=0.9'];
NAME{7} = ['h=9,T=55,v=0.9'];
NAME{8} = ['h=12,T=55,v=0.9'];
NAME{9} = ['T=45,v=0.9,h=3'];  
NAME{10}= ['T=55,v=0.9,h=3'];
NAME{11}= ['T=65,v=0.9,h=3'];
NAME{12}= ['T=60,v=0.9,h=3'];
NAME{13}= ['T=50,v=0.9,h=3']; 
 
for i = 1:13;
    figure;
    subplot(211);
    plot(y1{i},'ro');
    hold on
    plot(Train_output1{i},'b');
    xlabel('times');
    ylabel('水分比');
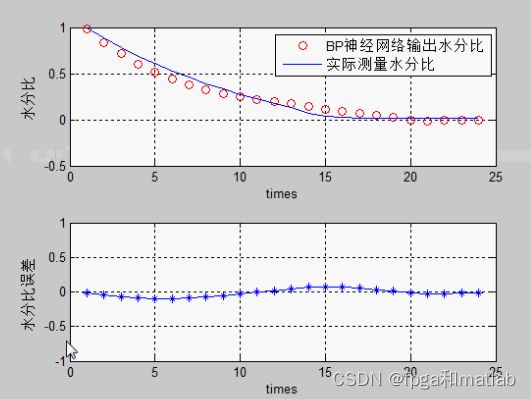
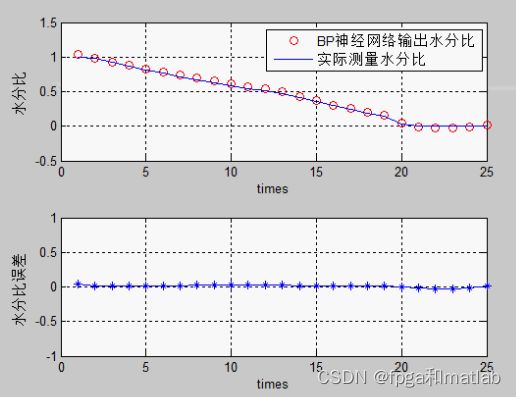
    legend('BP神经网络输出水分比','实际测量水分比');
    title(NAME{i});
    grid on
    subplot(212);
    plot(y1{i}-Train_output1{i}' ,'b-*');
    xlabel('times');
    ylabel('水分比误差');
    grid on
    ylim([-1,1]);
end

%风速变化显示
figure;
subplot(121);
plot(y1{1},'r-o');
hold on
plot(y1{2},'b-s');
hold on
plot(y1{3},'k-*');
hold on
plot(y1{4},'m-^');
hold on
xlabel('times');
ylabel('水分比');
legend('T=55,v=0.3,h=3','T=55,v=0.6,h=3','T=55,v=0.9,h=3','T=55,v=1.2,h=3');
grid on
title('BP神经网络输出');
ylim([0,1.2]);
subplot(122);
plot(Train_output1{1},'r-o');
hold on
plot(Train_output1{2},'b-s');
hold on
plot(Train_output1{3},'k-*');
hold on
plot(Train_output1{4},'m-^');
hold on
xlabel('times');
ylabel('水分比');
legend('T=55,v=0.3,h=3','T=55,v=0.6,h=3','T=55,v=0.9,h=3','T=55,v=1.2,h=3');
grid on
title('测量值');
grid on
ylim([0,1.2]);

%厚度变化显示
figure;
subplot(121);
plot(y1{5},'r-o');
hold on
plot(y1{6},'b-s');
hold on
plot(y1{7},'k-*');
hold on
plot(y1{8},'m-^');
hold on
xlabel('times');
ylabel('水分比');
legend('h=3,T=55,v=0.9','h=6,T=55,v=0.9','h=9,T=55,v=0.9','h=12,T=55,v=0.9');
grid on
title('BP神经网络输出');
ylim([0,1.2]);
subplot(122);
plot(Train_output1{5},'r-o');
hold on
plot(Train_output1{6},'b-s');
hold on
plot(Train_output1{7},'k-*');
hold on
plot(Train_output1{8},'m-^');
hold on
xlabel('times');
ylabel('水分比');
legend('h=3,T=55,v=0.9','h=6,T=55,v=0.9','h=9,T=55,v=0.9','h=12,T=55,v=0.9');
grid on
title('测量值');
grid on
ylim([0,1.2]);

%温度变化显示
figure;
subplot(121);
plot(y1{9},'r-o');
hold on
plot(y1{10},'b-s');
hold on
plot(y1{11},'k-*');
hold on
plot(y1{12},'m-^');
hold on
plot(y1{13},'c->');
hold on
xlabel('times');
ylabel('水分比');
legend('T=45,v=0.9,h=3','T=55,v=0.9,h=3','T=65,v=0.9,h=3','T=60,v=0.9,h=3','T=50,v=0.9,h=3');
grid on
title('BP神经网络输出');
ylim([0,1.2]);
subplot(122);
plot(Train_output1{9},'r-o');
hold on
plot(Train_output1{10},'b-s');
hold on
plot(Train_output1{11},'k-*');
hold on
plot(Train_output1{12},'m-^');
hold on
plot(Train_output1{13},'c->');
hold on
xlabel('times');
ylabel('水分比');
legend('T=45,v=0.9,h=3','T=55,v=0.9,h=3','T=65,v=0.9,h=3','T=60,v=0.9,h=3','T=50,v=0.9,h=3');
grid on
title('测量值');
grid on
ylim([0,1.2]);

 

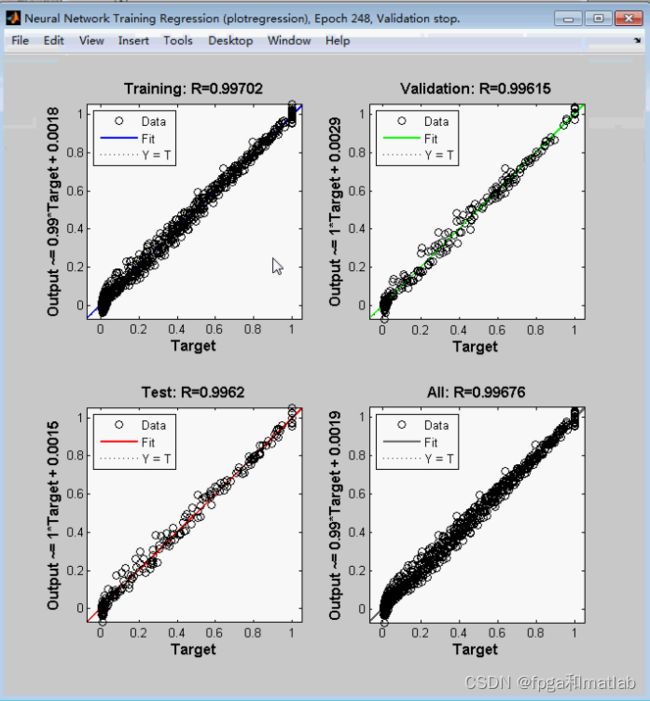
三、测试结果

 

 

 A05-60