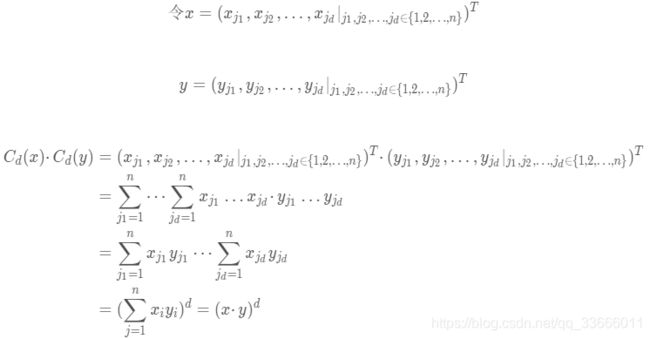2019.7学习总结-目标检测-Python+pytorch
目录
1、基础知识
1.1、dict的copy:
1.2、torch.cuda.synchronize()
1.3、在CenterNet里
1.4、torch.gather、topk用法:
1.5、torch常用的函数
1.6 torch.gather实现找3维度的Index
1.7、pytorch的modelz的parameter
2、kernel
2.1、核函数
2.2 不同的核函数
3、graph kernel
4、随机游走
1、基础知识
1.1、dict的copy:
dict直接赋值是深拷贝。同样使用from copy import deepcopy()也是深拷贝。而使用copy()是浅拷贝。
深拷贝,原始改动副本不变。浅拷贝原始改动副本也改动
j={'c':1,'g':2}
p=j.copy()
j['c']=5
print("使用.copy()是浅拷贝",'\n',"只是简单讲第一个dict的地址copy过去。所以原始改动,这个也改")
for k,v in p.items():
print(k,v)
u = j
j['c'] = 5
print("直接赋值是深拷贝", '\n', "原始改动,这个不改")
for k, v in u.items():
print(k, v)
from copy import deepcopy
h=deepcopy(j)
j['c'] = 55
print("使用deepcopy()是深拷贝")
for k, v in h.items():
print(k, v)输出结果:
但是在pytorch里,经过nn.Moduel得到的output(返回值),内部存在tensor类型的。是不可以深拷贝的。默认是浅拷贝。而deepcopy会报错。只能对Input运算之后赋值给output。不能改变其中某个值,之后副本不改。
两种情况:第一种:model的深拷贝
model2=model1 #会出现当更新model2时,model1的权重也会更新,这和自己的初始目的不同。
所有要使用下面的编写方法不会影响原始模型的权重
torch.save(model, "net_params.pkl")
model5=Cnn(3,10)
model5=torch.load('net_params.pkl')
第二种:output的深拷贝
model:forward() 操作之后赋予的变量是不给这个变量开盘新的存储空间的,而是 引用。就相当于 起了个别名。
改进:使用 y1=model:forward(x1) :clone()
此外,torch里面向量或是矩阵的赋值是指向同一内存的,这种策略不同于 Matlab。如果想不想引用,可以用 clone() 进行 深拷贝
1.2、torch.cuda.synchronize()
转载于https://blog.csdn.net/u013548568/article/details/81368019
torch.cuda.synchronize()
start = time.time()
result = model(input)
torch.cuda.synchronize()#如果没有这句话是不准确的,两者的时间可能不一样
end = time.time()在pytorch里面,程序的执行都是异步的。不加这句话,测试的时间会很短,因为执行完end=time.time()程序就退出了,后台的cu也因为python的退出退出了,如果加上这句话,代码会同步cu的操作,等待gpu上的操作都完成了再继续成形end = time.time()
start = time.time()
result = model(input)
print(result)
end = time.time()这时候会发现这段代码和上面加上torch.cuda.synchronize() 代码的时间是类似的,因为这段代码会等待gpu上的结果执行完传给print函数,所以真个的时间就和第二段同步的操作的时间基本上是一致的了,将print(result)换成result.cpu()结果是一致的惹。
1.3、在CenterNet里
,使用这样一种不同的nms方法。基于CenterNet对每一个点都进行预测的原因:heat = _nms(heat)
def _nms(heat, kernel=3):
pad = (kernel - 1) // 2
hmax = nn.functional.max_pool2d(
heat, (kernel, kernel), stride=1, padding=pad)
keep = (hmax == heat).float()
return heat * keepheat是(b_s,20,96,96)原图是384*384的。之后相当于对于12*12这个区域里预测得到的3*3个框, 首先找max值。之后等于max的那个值的对应的框保留,剩下框不保留。这一的nms
(是否可以改进?这样一定会去掉其中的重叠严重的相同类别的那些不同目标的框)可否不让其乘keep 或 keep不是max的那些点不是0,是一个小数。实验:效果不好。还是直接给0好
CenterNet中存在cat_spec_wh这个变量在lib/models/decode.py文件里。说明作者尝试过给每一个类别一个框的方法(因为某种原因没有最终使用)
CenterNet里根据
bboxes = torch.cat([xs - wh[..., 0:1] / 2,
ys - wh[..., 1:2] / 2,
xs + wh[..., 0:1] / 2,
ys + wh[..., 1:2] / 2], dim=2)预测的hm是score,wh是2维,reg是2维。根据点初始位置可以得到中心点(xs,ys),根据reg将中心点做偏移(reg[0]+xs,reg[1]+ys)得到新的中心点。之后得到边框中心点向左向右分别偏移wh[0],向上向下分别偏移wh[1]得到框。
预测4个并不一定好。因为预测了reg。如果再预测4个值,那么偏移的结果就不是唯一的解了。因为reg改变的时候wh也可以改变这样结果就不唯一了。
1.4、torch.gather、topk用法:
在CenterNet里我们通过 topk_scores, topk_inds = torch.topk(scores.view(b_s, 20, -1), 100)
topk_inds=topk_inds%(scores.shape[2],scores.shape[3])
得到每个类别score最大的分别100个点。及得到(b_s,20,100)的topk_inds。
并且通过 topk_score, topk_ind = torch.topk(topk_scores.view(b_s, -1), 100)
topk_clses = (topk_ind / K).int()得到整张图片score最大的前100个点在topk_scores里的位置的topk_ind ,并且这100个点分别最可能是什么类别的topk_clses(b_s,100)
ind=topk_ind.unsqueeze(2).expand(topk_ind.size(0), topj_ind.size(1), dim) feat=topk_inds.view(batch, -1, dim)feat = feat.gather(1, ind)就可以得到topk_inds里对应的topk_ind那个index位置里的内容
1)torch.topk(input, k, dim=None, largest=True, sorted=True, out=None) -> (Tensor, LongTensor)
沿给定dim维度返回输入张量input中 k 个最大值。
如果不指定dim,则默认为input的最后一维。
如果为largest为 False ,则返回最小的 k 个值。
返回一个元组 (values,indices),其中indices是原始输入张量input中测元素下标。
如果设定布尔值sorted 为_True_,将会确保返回的 k 个值被排序。
2)torch.gather(input, dim, index, out=None) → Tensor
a = torch.Tensor([[1,2],[3,4]])
[torch.FloatTensor of size 2x2]
b = torch.gather(a,1,torch.LongTensor([[0,0],[1,0]]))
1 1
4 3 [torch.FloatTensor of size 2x2]
!!!特别注意一下,index的类型必须是LongTensor类型的。
1.5、torch常用的函数
(https://www.jianshu.com/p/54708c840ec4)
在pyTorch中,函数名都是小写,类名的首字母大写。
torch.arange()和torch.range()的区别:
torch.arange(start, end, step) 返回一个以start为首项, 以end为尾项,以step为公差的等差数列。"不包含end"
torch.range(start, end, step) 返回一个以start为首项, 以end为尾项,以step为公差的等差数列。"但是包含end"
另外,torch.linspace(start, end, steps) 也可以返回一个等差数列,但是该数列以start 为起点,以end为终点,等间距地取steps个数。(包含start和end)
(1)张量的重排
tensor.reshape(r, c, k) 将张量tensor各个维度的大小改变为(r, c, k)
tensor.squeeze() 表示将张量tensor中大小为1的维度去掉
tensor.unsqueeze(dim) 表示在张量tensor指定的维度dim上增加一个大小为1的维度
tensor.permute(2, 0, 1,3) 表示对张量tensor的维度进行重新排列
tensor.transpose(0, 2) 表示将张量tensor指定的两个维度0 和 2 进行互换
(2)张量中部分数据的选择
tensor.index_select(1, [1, 4, 5]) 表示将张量tensor第二个维度,索引为1,4,5的数据挑选出来,其余数据丢掉
tensor.masked_select(mask) 其中mask是一个与tensor大小相同的张量,且其所有元素为1或者0,该函数的作用是将mask张量中值为1的位置的数据挑选出来,将其余数据丢掉,返回值由挑选出来的元素组成的1维张量。
(3)张量的扩张与拼接
tensor.repeat(x, y, z) 表示将张量tensor在三个维度上分别重复x, y, z次, 重复之后只是各个维度元素的数量增加了,张量的维度并没有改变
torch.cat([t1, t2], k) 表示将张量他t1和t2在维度k上进行拼接,注意:拼接完后张量的维度并没有变化。
torch.stack([t1, t2], k) 表示将张量t1和t2在维度k上进行拼接,拼接之后维度会增加1。 这种方式要求被拼接的张量t1, t2必须大小形状相同,增加的维度的大小等于拼接的张量的个数。
tensor.expand(x, y, z ...) 表示将张量tensor进行扩张,例如:
>>> x = torch.Tensor([[1], [2], [3]])
>>> x.size()
torch.Size([3, 1])
>>> x.expand(3, 4)
tensor([[ 1., 1., 1., 1.],
[ 2., 2., 2., 2.],
[ 3., 3., 3., 3.]])
(4)scatter 函数和gather函数
torch.gather(input, dim, index, out=None) → Tensor 聚集操作
沿给定轴 dim ,将输入索引张量 index 指定位置的值进行聚合,对一个 3 维张量,输出可以定义为:
out[i][j][k] = input[index[i][j][k]][j][k] # if dim == 0
out[i][j][k] = input[i][index[i][j][k]][k] # if dim == 1
out[i][j][k] = input[i][j][index[i][j][k]] # if dim == 2
如果 input 是 size 为 (x0,x1...,xi−1,xi,xi+1,...,xn−1) 且 dim = i 的 n 维张量,则 index 必须是具有 size 为 (x0,x1,...,xi−1,y,xi+1,...,xn−1) 的 n 维张量,其中 y >= 1 ,并且 out 将与 index 的 size 相同
>>> t = torch.Tensor([[1,2],[3,4]])
>>> torch.gather(t, 1, torch.LongTensor([[0,0],[1,0]]))
1 1
4 3 [torch.FloatTensor of size 2x2]
torch.Tensor scatter_(dim, index, src) → Tensor分散操作
从张量src中按照index张量中指定的索引位置写入self张量的值。对于一个三维张量,self更新为:
self[index[i][j][k]][j][k] = src[i][j][k] # if dim == 0
self[i][index[i][j][k]][k] = src[i][j][k] # if dim == 1
self[i][j][index[i][j][k]] = src[i][j][k] # if dim == 2
将张量src中的各个元素,按照index张量中指定的索引位置,写入到张量Tensor中。此函数中index张量的大小一般大于或等于src张量。
Example::
>>> x = torch.rand(2, 5)
>>> x
tensor([[ 0.3992, 0.2908, 0.9044, 0.4850, 0.6004],
[ 0.5735, 0.9006, 0.6797, 0.4152, 0.1732]])
>>> torch.zeros(3, 5).scatter_(0, torch.tensor([[0, 1, 2, 0, 0], [2, 0, 0, 1, 2]]), x)
tensor([[ 0.3992, 0.9006, 0.6797, 0.4850, 0.6004],
[ 0.0000, 0.2908, 0.0000, 0.4152, 0.0000],
[ 0.5735, 0.0000, 0.9044, 0.0000, 0.1732]])
>>> z = torch.zeros(2, 4).scatter_(1, torch.tensor([[2], [3]]), 1.23)
>>> z
tensor([[ 0.0000, 0.0000, 1.2300, 0.0000],
[ 0.0000, 0.0000, 0.0000, 1.2300]])
例如,该函数可以用来进行one-hot编码:
y_vec_ = torch.zeros((self.batch_size, self.class_num)).scatter_(1, y_.type(torch.LongTensor).unsqueeze(1), 1)
其中,class_num=10, y_= [ 5, 2, 6, 2, 9, 3, 0, 8, 2, ...... ] 的数字向量, y_vec便是对y_进行one-hot编码的结果。
(5)张量的初等运算
加法 + , 减法 - , 乘法 * , 除法 / , 乘方 **k , 开方 ** 。 这些运算要求参与运算的张量必须大小形状相同,张量的这些运算都是逐个元素进行运算,运算的结果为大小和形状都相同的张量。
(6)使用GPU进行运算
首先,可以根据语句 torch.cuda.is_available() 的返回值来判断GPU是否可用;通过torch.cuda.device_count()可以获得能够使用的GPU数量。然后调用GPU进行运算的方法为:
1)通过cuda() 方法将Tensor迁移到现存中去,具体操作为: Tensor.cuda()
2)使用.cuda() 将Variable迁移到显存中去,具体操作为:Variable.cuda()
3)对于模型来说,也是同样的方式,使用.cuda() 方法可以将网络模型放到显存上去, 具体操作为: model.cuda()
(7)使用指定的GPU运算
1)通过以下语句设置使用的GPU的id
import os
os.environ["CUDA_VISIBLE_DEVICES"] ="id"
2)使用函数set_device
import torch
torch.cuda.set_device(id)
(8)同时使用多GPU进行训练
Pytorch 的多 GPU 处理接口是torch.nn.DataParallel(module, device_ids),其中module参数是所要执行的模型,而device_ids则是指定并行的 GPU id 列表。
1.6 torch.gather实现找3维度的Index
首先使用Unsequeeze和expand,将2维的Index变为3维度。使Index的第一维和第三维与原值的维度相同。在第二维度索引相当于g里面的第二个通道上。每个都取的是
b=torch.Tensor([[0,1],[1,2],[2,3]]) #(3,2) 相当于 (b_s,2000)
b=b.unsqueeze(1).expand(3,5,2).permute(0,2,1) # 相当于 (b_s,2000,20)
g=torch.arange(3*4*5).reshape(3,4,5) # 相当于 (b_s,96*96,20)
p=g.gather(dim=1,index=b.long())
print(p.size()) # 相当于 (b_s,2000,20)
结果:
g: tensor([[[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]],
[[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29],
[30, 31, 32, 33, 34],
[35, 36, 37, 38, 39]],
[[40, 41, 42, 43, 44],
[45, 46, 47, 48, 49],
[50, 51, 52, 53, 54],
[55, 56, 57, 58, 59]]])
b: torch.Size([3, 2, 5])
p: tensor([[[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9]],
[[25, 26, 27, 28, 29],
[30, 31, 32, 33, 34]],
[[50, 51, 52, 53, 54],
[55, 56, 57, 58, 59]]])1.7、pytorch的modelz的parameter
pytorch model.named_parameters() ,model.parameters() ,model.state_dict().items()
for name, param in model.named_parameters():
print(name,param.requires_grad)
param.requires_grad=False #既打印名字也打印参数值
for param in model.parameters():
print(param.requires_grad)
param.requires_grad=False//只打印参数值
model.state_dict().items() 每次迭代打印该选项的话,会打印所有的name和param,但是这里的所有的param都是requires_grad=False,没有办法改变requires_grad的属性,所以改变requires_grad的属性只能通过上面的两种方式。
for name, param in model.state_dict().items():
print(name,param.requires_grad=True)
部分网络层的lr不一样
optimizer = optim.SGD(
filter(lambda p: p.requires_grad, model.parameters()), #只更新requires_grad=True的参数
lr=cfg.TRAIN.LR,
momentum=cfg.TRAIN.MOMENTUM,
weight_decay=cfg.TRAIN.WD, )
随机参数初始化
def init_weights(m):
if isinstance(m, nn.Conv2d):
torch.nn.init.xavier_uniform(m.weight.data)
model.apply(init_weights)2、kernel
2.1、核函数
1)例子:
核函数K(kernel function)就是指K(x, y) =
举个小小栗子。
令 x = (x1, x2, x3, x4); y = (y1, y2, y3, y4);
令 f(x) = (x1x1, x1x2, x1x3, x1x4, x2x1, x2x2, x2x3, x2x4, x3x1, x3x2, x3x3, x3x4, x4x1, x4x2, x4x3, x4x4); f(y)亦然;
令核函数 K(x, y) = (
接下来,让我们带几个简单的数字进去看看是个什么效果:x = (1, 2, 3, 4); y = (5, 6, 7, 8). 那么:
f(x) = ( 1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12, 4, 8, 12, 16) ;
f(y) = (25, 30, 35, 40, 30, 36, 42, 48, 35, 42, 49, 56, 40, 48, 56, 64) ;
= 4900.
如果我们用核函数呢?
K(x, y) = (5+12+21+32)^2 = 70^2 = 4900.
就是这样!
所以现在你看出来了吧,kernel其实就是帮我们省去在高维空间里进行繁琐计算的“简便运算法”。甚至,它能解决无限维空间无法计算的问题!因为有时f(·)会把n维空间映射到无限维空间去。
什么时候我们会把n维度向量映射到无限维空间呢?比如:SVM
2)核函数
无法在原始空间(Rd)中适当的找到一个线性分类器将两类区隔开,这时后此需要找到一个非线性投影(φ)将特征进行转换到更高维度的空间,此时在高维度的空间中只需要一个线性分类器/hyperplane就可以完美分类。而这个更高维度的空间则称为Hilbert space(H)。但我们又很难直接去设计一个好的非线性投影(φ)公式,因此需要kernel函数来辅助。这个过程就是SVM。
支持向量机通过某非线性变换 φ( x) ,将输入空间映射到高维特征空间来实现了线性可分。特征空间的维数可能非常高。如果支持向量机的求解只用到内积运算,而在低维输入空间又存在某个函数 K(x, x′) ,它恰好等于在高维空间中这个内积,即K( x, x′) =<φ( x) ⋅φ( x′) > 。那么支持向量机就不用计算复杂的非线性变换,而由这个函数 K(x, x′) 直接得到非线性变换的内积,使大大简化了计算。这样的函数 K(x, x′) 称为核函数。
核函数:是映射关系![]() 的内积,映射函数本身仅仅是一种映射关系,并没有增加维度的特性,不过可以利用核函数的特性,构造可以增加维度的核函数,这通常是我们希望的。
的内积,映射函数本身仅仅是一种映射关系,并没有增加维度的特性,不过可以利用核函数的特性,构造可以增加维度的核函数,这通常是我们希望的。
二维映射到三维,区分就更容易了,这是聚类、分类常用核函数的原因。为什么PCA这样一个降维算法也用核函数呢?
左图为原数据,右图为映射到三维的数据,可以看出:同样是降到1维,先通过Kernel映射到(Kernel是映射的内积,不要弄乱了)三维,再投影到1维,就容易分离开,这就是Kernel在PCA降维中的应用,本质还是对原有数据增加维度。
那么在高维空间中,样本数据很有可能线性可分,这个特点可以用下图做一个很好的说明:
![]()
如左图,红色部分的点为一类数据,黑色部分的点为另一类,在一维空间中,你不可能通过一刀切将两类数据分开,至少需要两刀。OK,这就说明数据分布是非线性的,我们采用高维映射,当然了,例子中只是映射到了二维空间,但已经足够说明问题了,在右图中,完全可以通过沿着X轴方向的一刀切将两类数据分开,说明在二维空间中,数据已经变成线性可分的了。
下面是李航的《统计学习方法》中对于核函数的定义:
![]()
要注意,核函数和映射没有关系。核函数只是用来计算映射到高维空间之后的内积的一种简便方法。
这个公式表达的意思只是高维空间中向量的内积等于原空间中向量之间的核函数的内积值,根核函数的具体形式没有一毛钱的关系。意味着如果用核函数来降低计算量。那么核函数需要满足这个条件。
满足多维数据的內积即可使用核函数进行解决。(在我们求相似度的时候常用内积)
2.2 不同的核函数
1)Mercer 定理:
任何半正定的函数都可以作为核函数。所谓半正定的函数f(xi,xj),是指拥有训练数据集合(x1,x2,...xn),我们定义一个矩阵的元素aij = f(xi,xj),这个矩阵式n*n的,如果这个矩阵是半正定的,那么f(xi,xj)就称为半正定的函数。
正定: AA 是n阶方阵,如果对任何非零向量xx,都有xTAx>0xTAx>0,其中xTxT 表示xx的转置,就称AA正定矩阵。
性质: 正定矩阵的行列式恒为正;
实对称矩阵AA正定当且仅当AA与单位矩阵合同;
两个正定矩阵的和是正定矩阵;
正实数与正定矩阵的乘积是正定矩阵。
请注意,这个mercer定理不是核函数必要条件,只是一个充分条件,即还有不满足mercer定理的函数也可以是核函数。所谓半正定指的就是核矩阵K的特征值均为非负。
2)核函数的选择:
![]()
假设,a是-0.5,b是2.7.可以选择核函数K(x,y)映射为x->x平方 (-0.5,0,0.5,1,2.7)这样的数变成了((-0.5,2.5),(0,0),(0.25*0.25),(1,1),(2.7,7.29))这样的二维度数据。而可以这样变化的原因在于:-0.5*1 在映射之后(-0.5,2.5)*(1,1)=-0.5 映射之后内积不变,意味着原来不同数据之间的关系不变,因此这个映射过程是合理的,同时因为内积相同。在我们映射到高维度可以线性可分,内积仍然可以使用低纬度的数值进行计算。之后使用一个线性的判别式,g(x))=kx+b 来进行判别。(在二维空间里直线是线性的判别式)而如果我们选更高维的,如变成3维度,可能就不是很好分别了。所以如何确定核函数是很复杂的问题。
例子:我们原始样本特征维度为2,将其映射到三维空间,假设我们的映射函数为f(x1,x2) = (x1^2, x2^2, 2*x1*x2),那么在三维空间中,样本线性可分更大,但是向量内积的计算开销从4((a1,a2)*(b1,b2) 一共4步计算)提高到9((a1,a2,a3)*(b1,b2,b3) 一共9步计算)【如果从10维映射到1000维,那么计算花销就提高了10000倍,而实际情况下,特征维度几万上百万十分常见】,再看对于样本n1=(a1,a2),n2=(b1,b2),映射到三维空间之后,两者的内积I1为:a1^2 * b1^2 + a2^2 * b2^2 + 4 * a1 * a2 * b1 * b2,此时,又有,n1,n2在二维空间中的内积为:a1b1 + a2b2,平方之后为I2:a1^2 * b1^2 + a2^2 * b2^2 + 4 * a1 * a2 * b1 * b2,此时 I1 和 I2 是不是很相似,只要我们将f(x1,x2)调整为: (x1^2, x2^2, 根号(2*x1*x2) ) ,那么此时就有I1 = I2,也就是说,映射到三维空间里的内积,可以通过二维空间的内积的平方进行计算! 而这个找到合适的映射就一方面可以线性可分了,一方面计算仍旧可以使用低维数据进行计算,所以是一个很好的方法。而重点就是找到一个映射,也可以说找到一个核函数使得可以让数据线性可分,同时可以保证内积不变。
(注意:y=ax 如果x是3维度,那么这个y=ax是4维的函数)
将核函数形式化定义,如果原始特征内积是![]() ,映射后为
,映射后为![]() ,那么定义核函数(Kernel)为:
,那么定义核函数(Kernel)为:
![]()
实际上对于复杂的问题核函数还是挺难找的,目前常用的有多项式核,高斯核,还有线性核。
3)几种常见的核函数
Linear Kernel
线性核是最简单的核函数,核函数的数学公式如下:![]()
Polynomial Kernel
多项式核实一种非标准核函数,它非常适合于正交归一化后的数据,其具体形式如下:![]()
这个核函数是比较好用的,就是参数比较多,但是还算稳定。
Gaussian Kernel
这里说一种经典的鲁棒径向基核,即高斯核函数,鲁棒径向基核对于数据中的噪音有着较好的抗干扰能力,其参数决定了函数作用范围,超过了这个范围,数据的作用就“基本消失”。高斯核函数是这一族核函数的优秀代表,也是必须尝试的核函数,其数学形式如下:![]()
虽然被广泛使用,但是这个核函数的性能对参数十分敏感,以至于有一大把的文献专门对这种核函数展开研究,同样,高斯核函数也有了很多的变种,如指数核,拉普拉斯核等。
Exponential Kernel
指数核函数就是高斯核函数的变种,它仅仅是将向量之间的L2距离调整为L1距离,这样改动会对参数的依赖性降低,但是适用范围相对狭窄。其数学形式如下:![]()
Laplacian Kernel
拉普拉斯核完全等价于指数核,唯一的区别在于前者对参数的敏感性降低,也是一种径向基核函数。![]()
ANOVA Kernel
ANOVA 核也属于径向基核函数一族,其适用于多维回归问题,数学形式如下:![]()
Sigmoid Kernel
Sigmoid 核来源于神经网络,现在已经大量应用于深度学习,是当今机器学习的宠儿,它是S型的,所以被用作于“激活函数”。关于这个函数的性质可以说好几篇文献,大家可以随便找一篇深度学习的文章看看。![]()
Rational Quadratic Kernel
二次有理核完完全全是作为高斯核的替代品出现,如果你觉得高斯核函数很耗时,那么不妨尝试一下这个核函数,顺便说一下,这个核函数作用域虽广,但是对参数十分敏感,慎用!!!!![]()
4)多项式核函数
可以看出该核函数--二次项多项式核函数,K(x1,x2)=(x1*x1,x2*x2,x1*x2,x2*x1)是ok的因为内积相等。多次项多项式核函数同理
5)所谓径向基函数 (Radial Basis Function 简称 RBF)
就是某种沿径向对称的标量函数。 通常定义为空间中任一点x到某一中心xc之间欧氏距离的单调函数 ,可记作 k(||x-xc||), 其作用往往是局部的 , 即当x远离xc时函数取值很小。
最常用的径向基函数是高斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/(2*σ)^2) } 其中x_c为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。如果x和x_c很相近那么核函数值为1,如果x和x_c相差很大那么核函数值约等于0。由于这个函数类似于高斯分布,因此称为高斯核函数,也叫做径向基函数(Radial Basis Function 简称RBF)。它能够把原始特征映射到无穷维。
高斯核函数能够比较x和z的相似度,并映射到0到1,回想logistic回归,sigmoid函数可以,因此还有sigmoid核函数等等。
3、graph kernel
kernel method 在图结构中的研究主要有两类:
一是Graph embedding 算法,将图(Graph)结构嵌入到向量空间,得到图结构的向量化表示,然后直接应用基于向量的核函数(RBF kernel, Sigmoid kernel, etc.) 处理,但是这类方法将结构化数据降维到向量空间损失了大量结构化信息;
二是Graph kernel算法, 直接面向图结构数据,既保留了核函数计算高效的优点,又包含了图数据在希尔伯特高维空间的结构化信息,针对不同的图结构(labeled graphs, weighted graphs, directed graphs, etc.) 有不同的Graph kernel。
随机游走核:在两个graph上随机游走,计算核函数,比较两个图的相似性
4、随机游走
基本的随机游走:每次随机选择一个当前解的邻域点进行比较,如果优于当前解则将该点作为新的中心。如果连续N次都找不到更优的值,则认为,最优解就在以当前最优解为中心,当前步长为半径的N维球内(如果是三维,则刚好是空间中的球体)。此时,如果步长已经小于阈值,则结束算法;否则,令步长减半,开始新一轮游走。
改进的随机游走算法:不同之处是在于原来是产生一个随机向量u,现在则是产生n个随机向量u1,u2,⋯,un,n是给定的一个正数。通过这种方式改进之后,随机游走算法的寻优能力大大提高,而且对于初始值的依赖程度也降低了。