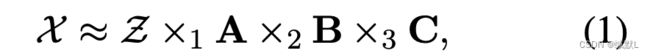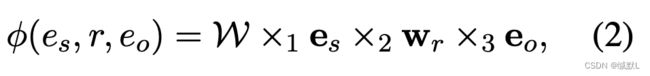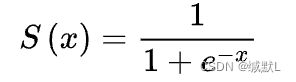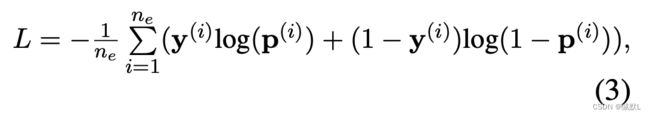知识图谱补全论文阅读笔记：TuckER: Tensor Factorization for Knowledge Graph Completion

摘要：

链接预测是一项基于现有事实推断缺失事实的任务。

tucker分解是三元组的二元t二进制三阶张量ensor表示（这个翻译是错误的，按照下面的上下文，binary tensor representation应该是翻译成二进制三阶张量）。

当时来说TuckER在标准链路预测数据集中的表现优于以前最先进（state-of-the-art）的模型。

这是一个fully expressive model（完全表达的）线性模型，并且说明了之前的线性模型是它的变体或者说特殊情况。

1介绍：

        知识图谱是大型的图结构数据库，（es、r、eo）存储事实。目前，所有可用信息都存储在现有的知识图谱中，手动添加新信息的成本很高，这就产生了对能够自动推断缺失事实的算法的需求。

        知识图谱可以表示为二进制三阶张量，其中的每个元素对应对应一个三元组（事件）。1 表示真实事实，0 表示未知事实（虚假事实或遗漏事实）。链接预测的任务是根据知识图中已经存在的已知事实来预测两个实体是否相关，即任务是，将0的未知事实进行处理，是否是虚假事实，或者是否是遗漏事实（真事实）。

        到目前为止，大量的链接预测方法都是线性的，基于分解二进制三阶张量的各种方法。最近，使用非线性卷积模型已经取得了最先进的结果（2018，2019）。虽然基于深度学习的非线形模型的效果很好，但是可解释性比较差。tensor模型基于数学原理，可以解决这个问题。

        TuckER（E代表实体，R代表关系），基于tucker分解简单线性模型并作为坚实的基础。tucker分解，广泛用于机器学习，其分解是将张量分解成核心张量并成各个模式的矩阵。在矩阵正交且核心张量为“全正交”的特殊情况下，它可以被认为是高阶SVD的一种形式。在文章中的例子中，矩阵表示的是实体和关系的嵌入，而核心张量表示的是他们的交互关系。文章中认为subject和object实体是等价的，不会依赖于是否是特殊的三元组。

        TuckER表达是完全的即给定三元组的任何基本真理，存在实体和关系嵌入的值符号，可以准确地将真三元组与假三元组区分开来。RESCAL（Nickel等人，2011），DistMult（Yang等人，2015），ComplEx（Trouillon等人，2016）和SimplE（Kazemi和Poole，2018）是TuckER的特殊情况。

        贡献：提出TuckER，一种新的线性模型，用于知识图谱的链接预测，简单，富有表现力，并在所有标准数据集上实现最先进的结果;证明 TuckER 是完全表达的，并在嵌入维度上推导出一个界限以获得完全的表现力;展示了 TuckER 如何包含几个先前提出的张量分解应用来链接预测。

2相关工作：        

介绍模型

3背景：

表示的是所有实体，R所有关系。（es,r,eo),三元组表示。

3.1链接预测

在链接预测中，我们得到了所有真三元组的子集，目的是学习评分函数φ。分配分数

S = φ（es， r， eo） ∈ R，指示三元组是否为真，最终目标是能够正确得分所有缺失的三元组。

3.2tucker分解

将张量分解为一个一个核心张量和三个矩阵

X n表示的是n模乘，因为A，B，C是矩阵，所以其又被称之为n模矩阵积。X1，X2，X3表示的是三个方向。

当A、B、C正交时，则认为A、B、C是每种模式的主要组合。Z反应不同分量之间的交互水平（可以理解为权重）

在上方的式子中，，X是P x Q x R 。A的维度是I x P，B是J x Q，C是K x R，Z是I x J x K

关于tucker的运算可以看这个包括什么是n-模乘积张量的概念及基本运算_ChihYuanTSENG的博客-CSDN博客_张量运算法则

通常，P，Q，R分别小于I，J，K，因此Z可以被认为是X的压缩版本。

Tucker分解不是唯一的，即如果我们将逆变换应用于 A、B 和 C，我们可以变换 Z 而不影响拟合。（tucker分解很灵活）

4tucker分解的链接预测

如何将tucker分解应用到链接中。

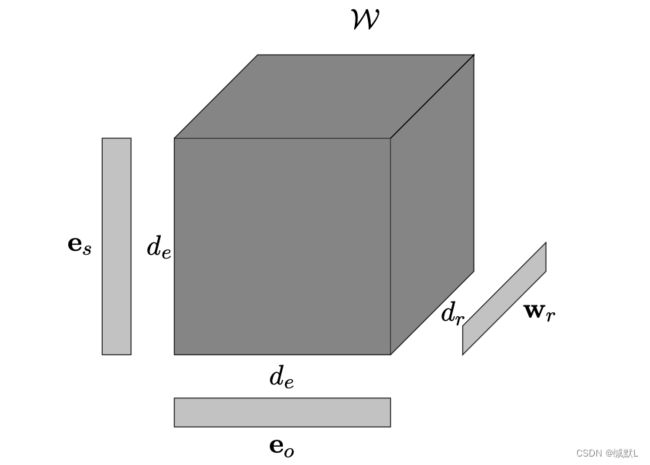
本文提出了一个模型，该模型使用tucker分解对知识图的二进制张量表示进行链接预测，实体嵌入矩阵E等效于主体和客体实体，即E = A = C ∈ R(ne×de)和关系嵌入矩阵R = B ∈ R(nr×dr)，其中ne和nr表示实体和关系的数量，de和dr表示实体和关系嵌入向量的维度。

个人理解的A是的矩阵中每一行表示一个实体，其行数据表示的就是一个实体的embedding。

 

 每一个切片中的元素的横纵表示实体，每一个切片表示的是一个关系。

该评分函数定义为

其中es，eo表示的是E的一行

在上述发的那篇博客中9.2有提到 n模向量积，由n模向量积可得这个评分函数是一个数。

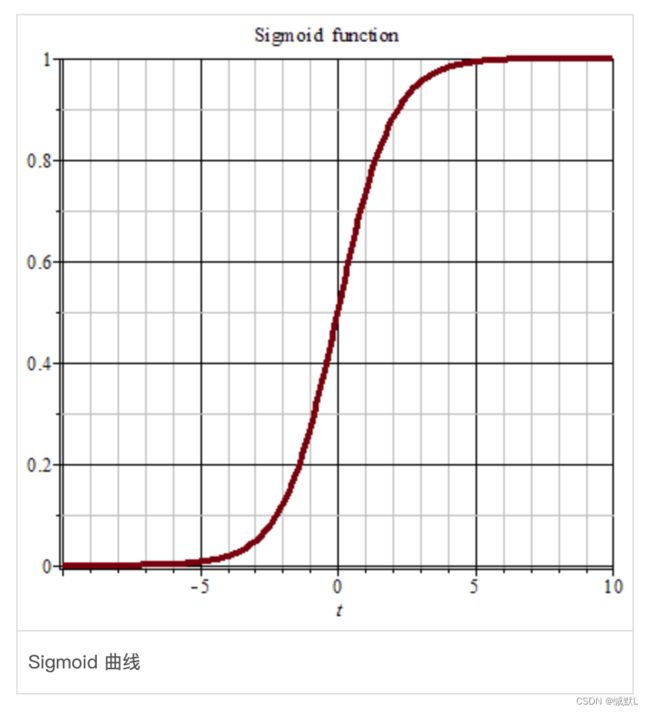
评分函数中的数会放到sigmoid函数中进行正确率都计算。

 

当评分函数(*)越大，越趋于1，概率中则是100%

此外，随着实体和关系数量的增加，其参数数量相对于实体和关系嵌入维度 de 和 dr 呈线性增加，因为 W 的参数数量仅取决于嵌入维度的实体和关系，而不取决于实体或关系的数量。（这句的意思大意应该是：数量 影响 维度    维度 影响 参数量）

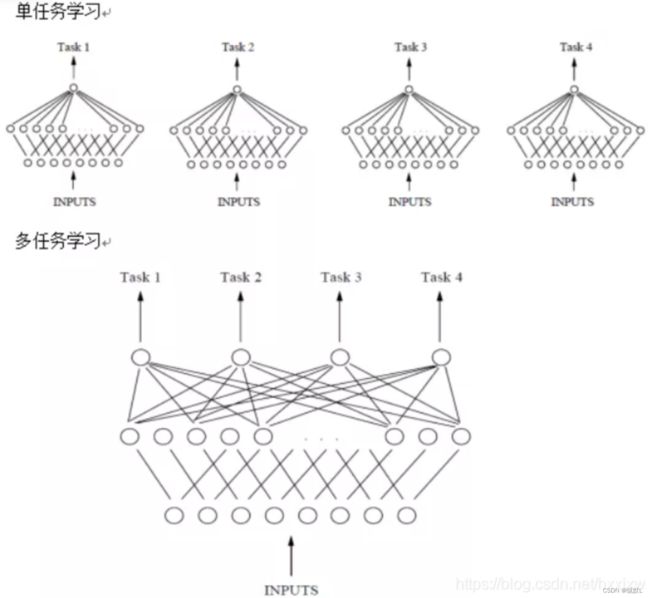
与DistMult，Com-plEx和SimplE等模型不同，TuckER具有核心张量W，不会将所有学习的知识编码到嵌入中;有些存储在核心张量中，并通过多任务学习在所有实体和关系之间共享。与其学习不同的关系特定矩阵，TuckER的核心张量可以被视为包含“原型”关系矩阵的共享池，这些矩阵根据每个关系嵌入中的参数线性组合。（这应该是tucker的优势）

多任务学习：Multi-task Learning(MTL) 多任务学习_hxxjxw的博客-CSDN博客_multi-task learning

4训练

由于 sigmoid 应用于评分函数以近似真正的二元张量，因此隐式底层张量由 −∞ 和 ∞ 组成（评分函数的值）。 

鉴于这阻止了显式的分析分解，我们使用数值方法来训练TuckER。（这句话我没有理解）

而后的操作，关于对每个类型的事实进行了对，其目的是对数据增强。

损失函数为：

这是一个二分类的交叉熵损失函数（主要是为了区分真和假的事实，前文提及）

5理论分析

后续是证明过程，可以看原文细看

6实验