蒙特卡洛三门问题及Python模拟

三门问题

参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门会否增加参赛者赢得汽车的机率？注意此处规定了主持人必开山羊的门，而不是随手开任意一道门！！！！

暴力穷举法解决：

概率问题里，有个很有用的笨办法就是穷举法。好在三门问题的事件有限，因此用穷举法正合适：

最开始1/3的概率选到车：换门能赢的概率是 1/3×0=0 ，不换门能赢的概率是 1/3×1=1/3。

最开始1/3的概率选到羊A：换门能赢的概率是1/3×1=1/3，不换门能赢的概率是1/3×0=0。

最开始1/3的概率选到羊B：换门能赢的概率是1/3×1=1/3，不换门能赢的概率是1/3×0=0。

可以看出来，不换门能赢的方法只有一个，就是选中汽车那扇门，概率是 1/3，而换门能赢的方法是选中有山羊的那扇门，概率是 2/3。

所以可以看出，在主持人必开山羊的门的条件下，换门和不换门赢的概率其实已经确定了，不随你什么时候做决策而改变。很多人认为选中不换，和主持人开门后再换，决策是有区别的，其实是被题目误导了，如果你最开始选中羊的门，换门必赢，不换必输；如果选中车的门，不换门必赢，换门必输。

代码如下：

import random


class MontyHallGame:
    def __init__(self, door_cnt=3):
        self.door_cnt = door_cnt  # door_cnt >= 3
        self.door_arr = [False] * door_cnt  # False: Goat, True: Car
        self.door_arr[random.randint(0, door_cnt - 1)] = True

    def play(self, select_idx, exchange):
        if exchange:
            # 不管几道门，最后都会只剩下两道门给你选择，互为对立面，一门有车，一门有羊
            # 选了车的，换门后就是羊；同理选了羊的，换门后就是车
            # 所以只要反转一下结果就行，不用再模拟主持人的开门操作了
            return not self.door_arr[select_idx]
        else:
            return self.door_arr[select_idx]


if __name__ == '__main__':
    game_times = 100000

    door_cnt = 3
    print('{}道门，换与不换各自都玩{}盘游戏'.format(door_cnt, game_times))

    # 不换门
    car_cnt = 0
    for i in range(game_times):
        game = MontyHallGame()
        select_door = random.randint(0, game.door_cnt - 1)
        result = game.play(select_door, False)
        car_cnt += 1 if result else 0
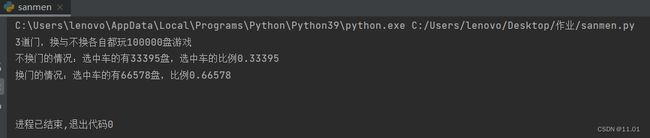
    print('不换门的情况：选中车的有{}盘，选中车的比例{}'.format(car_cnt, car_cnt / game_times))

    # 换门
    car_cnt = 0
    for i in range(game_times):
        game = MontyHallGame()
        select_door = random.randint(0, game.door_cnt - 1)
        result = game.play(select_door, True)
        car_cnt += 1 if result else 0
    print('换门的情况：选中车的有{}盘，比例{}'.format(car_cnt, car_cnt / game_times))

    print()

结果如下：