Connecting the Dots: Document-level Neural Relation Extraction with Edge-oriented Graphs 关系抽取论文总结
文章目录
-
- 往期文章目录链接
- Relation Extraction (RE)
-
- document-level RE
- Intuition
- Contribution
- Overview of Proposed Model
- Proposed Model
-
- Sentence Encoding Layer
- Graph construction Layer
-
- Node Construction
- Edge Construction
- Inference Layer
-
- First Step
- Second Step
- Classification Layer
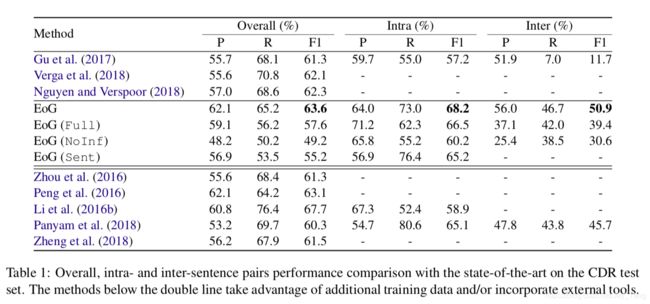
- Result
- Bad Cases Analysis
- 往期文章目录链接
往期文章目录链接
Relation Extraction (RE)
Relation Extraction (RE): The extraction of relations between named entities in text.

Relation Extraction is an important task of NLP. Most existing works focus on intra-sentence RE. In fact, in real-world scenarios, a large amount of relations are expressed across sentences. The task of identifying these relations is named inter-sentence RE.
Typically, inter-sentence relations occur in textual snippets with several sentences, such as documents. In these snippets, each entity is usually repeated with the same phrases or aliases, the occurrences of which are often named entity mentions and regarded as instances of the entity.
The multiple mentions of the target entities in different sentences can be useful for the identification of inter-sentential relations, as these relations may depend on the interactions of their mentions with other entities in the same document. The figure above is an good example of identifying the relationship between “ethambutol”, “isoniazid” and “scotoma”, where they all interact with the green colored entity (and its alias).
document-level RE
-
In concept, document-level RE the input is considered an annotated document. The annotations include concept-level entities as well as multiple occurrences of each entity under the same phrase of alias, i.e., entity mentions.
-
Objective: the objective of the task is given an annotated document, to identify all the related concept-level pairs in that document.
Document-level RE is not common in the general domain, as the entity types of interest can often be found in the same sentence. On the contrary, in the biomedical domain, document-level relations are particularly important given the numerous aliases that biomedical entities can have (as shown in the figure above).
Intuition
Graph-based neural approaches have proven useful in encoding long distance, inter-sentential information. These models interpret words as nodes and connections between them as edges. They typically perform on the nodes by updating the representations during training.
This paper: However, a relation between two entities depends on different contexts. It could thus be better expressed with an edge connection that is unique for the pair. A straightforward way to address this is to create graph-based models that rely on edge representations rather focusing on node representations, which are shared between multiple entity pairs.
Contribution
- We propose a novel edge-oriented graph neural model for document-level relation extraction, which encodes information into edge representations rather than node representations.
- Analysis indicates that the document-level graph can effectively encode document-level dependencies.
- we show that inter-sentence associations can be beneficial for the detection of intra-sentence relations.
Overview of Proposed Model
We presented a novel edge-oriented graph neural model (EoG) for document-level relation extraction using multi-instance learning. The proposed model constructs a document-level graph with heterogeneous types of nodes and edges, modelling intra- and inter-sentence pairs simultaneously with an iterative algorithm over the graph edges.
Here is an illustration of the abstract architecture of the proposed approach.

Proposed Model
The proposed model consists of four layers: sentence encoding, graph construction, inference and classification layers. The model receives a document (with identified concept-level entities and their textual mentions) and encodes each sentence separately. A document-level graph is constructed and fed into an iterative algorithm to generate edge representations between the target entity nodes.
Sentence Encoding Layer
We use a Bi-LSTM to encode each sentence and then get a contextualized word representations of the input sentence. The contextualized word representations from the encoder are then used to construct a document-level graph structure.
Graph construction Layer
Graph construction consists of Node Construction and Edge Construction.
Node Construction
They form three distinct types of nodes in the graph:
- Mention nodes (M) n m n_m nm. Mention nodes correspond to different mentions of entities in the input document. The representation of a mention node is formed as the average of the words ( w w w) that the mention contains, i.e. avg w i ∈ m ( w i ) \operatorname{avg}_{w_{i} \in m}\left(\mathbf{w}_{i}\right) avgwi∈m(wi).
- Entity nodes (E) n e n_e ne. Entity nodes represent unique entity concepts. The representation of an entity node is computed as the average of the mention ( m m m) representations associated with the entity, i.e. avg m i ∈ e ( m i ) \operatorname{avg}_{m_{i} \in e}\left(\mathbf{m}_{i}\right) avgmi∈e(mi).
- Sentence nodes (S) n s n_s ns. Sentence nodes correspond to sentences. A sentence node is represented as the average of the word representations in the sentence, i.e. avg w i ∈ s ( w i ) \operatorname{avg}_{w_{i} \in s}\left(\mathbf{w}_{i}\right) avgwi∈s(wi).
To distinguish different node types in the graph, they concatenate a node type ( t t t) embedding to each node representation. The final node representations are then estimated as n m = [ avg w i ∈ m ( w i ) ; t m ] , n e = \mathbf{n}_{m}=[\operatorname{avg}_{w_{i} \in m}\left(\mathbf{w}_{i}\right) ; \mathbf{t}_{m}], \mathbf{n}_{e}= nm=[avgwi∈m(wi);tm],ne= [ avg m i ∈ e ( m i ) ; t e ] , n s = [ avg w i ∈ s ( w i ) ; t s ] [\operatorname{avg}_{m_{i} \in e}\left(\mathbf{m}_{i}\right) ; \mathbf{t}_{e}], \mathbf{n}_{s}=[\operatorname{avg}_{w_{i} \in s}\left(\mathbf{w}_{i}\right) ; \mathbf{t}_{s}] [avgmi∈e(mi);te],ns=[avgwi∈s(wi);ts].
Edge Construction
We pre-define the following edge types:
-
Mention-Mention (MM): Mention-to-mention edges are connected if the corresponding mentions reside in the same sentence. The edge representation between each mention pair m i m_{i} mi and m j m_{j} mj is generated by concatenating the representations of the nodes, the contexts c m i , m j c_{m_{i}, m_{j}} cmi,mj and a distance embedding associated with the distance between the two mentions d m i , m j , d_{m_{i}, m_{j}}, dmi,mj, in terms of intermediate words: x M M = [ n m i ; n m j ; c m i , m j ; d m i , m j ] \mathbf{x}_{\mathbf{M M}} = [\mathbf{n}_{m_{i}} ; \mathbf{n}_{m_{j}} ; \mathbf{c}_{m_{i}, m_{j}} ; \mathbf{d}_{m_{i}, m_{j}}] xMM=[nmi;nmj;cmi,mj;dmi,mj], the context is calculated using
k ∈ { 1 , 2 } α k , i = n m k ⊤ w i a k , i = exp ( α k , i ) ∑ j ∈ [ 1 , n ] , j ∉ m k exp ( α k , j ) a i = ( a 1 , i + a 2 , i ) / 2 c m 1 , m 2 = H ⊤ a \begin{aligned} k &\in \{1,2\}\\ \alpha_{k, i} &=\mathbf{n}_{m_{k}}^{\top} \mathbf{w}_{i} \\ \mathrm{a}_{k, i} &=\frac{\exp \left(\alpha_{k, i}\right)}{\sum_{j \in[1, n], j \notin m_{k}} \exp \left(\alpha_{k, j}\right)} \\ \mathrm{a}_{i} &=\left(\mathrm{a}_{1, i}+\mathrm{a}_{2, i}\right) / 2 \\ \mathrm{c}_{m_{1}, m_{2}} &=\mathbf{H}^{\top} \mathrm{a} \end{aligned} kαk,iak,iaicm1,m2∈{1,2}=nmk⊤wi=∑j∈[1,n],j∈/mkexp(αk,j)exp(αk,i)=(a1,i+a2,i)/2=H⊤a where H ∈ R w × d \mathbf{H} \in \mathbb{R}^{w \times d} H∈Rw×d is a sentence word representations matrix. -
Mention-Sentence (MS): Mention-to-sentence nodes are connected if the mention is in the sentence. The initial edge representation is represented as x M S = [ n m ; n s ] \mathbf{x}_{\mathbf{MS}} = [\mathbf{n}_{m} ; \mathbf{n}_{s}] xMS=[nm;ns].
-
Mention-Entity (ME): Mention-to-entity nodes are connected if the mention is associated with the entity, x M E = [ n m ; n e ] \mathbf{x}_{\mathbf{ME}} = [\mathbf{n}_{m} ; \mathbf{n}_{e}] xME=[nm;ne].
-
Sentence-Sentence (SS): To encode the distance between sentences, they concatenate
to the sentence node representations their distance in the form of an embedding. They connect all sentence nodes in the graph, x M S = [ n s i ; n s j ; d s i , s j ] \mathbf{x}_{\mathbf{MS}} = [\mathbf{n}_{s_i} ; \mathbf{n}_{s_j}; \mathbf{d}_{s_i,s_j}] xMS=[nsi;nsj;dsi,sj]. -
Entity-Sentence (ES): Entity-to-sentence nodes are connected if at least one mention of the entity is in this sentence, x E S = [ n e ; n s ] \mathbf{x}_{\mathbf{ES}} = [\mathbf{n}_{e} ; \mathbf{n}_{s}] xES=[ne;ns].
Then there is a linear transformation to make sure each edge representation has the same dimension. For different edge representations, the dimension of the linear transformation layer is different: e z ( 1 ) = W z x z \mathbf{e}_{z}^{(1)}=\mathbf{W}_{z} \mathbf{x}_{z} ez(1)=Wzxz where e z ( 1 ) \mathbf{e}_{z}^{(1)} ez(1) is an edge representation of length 1. W z ∈ R d z × d \mathbf{W}_{z} \in \mathbb{R}^{d_{z} \times d} Wz∈Rdz×d corresponds to a learned matrix and z ∈ [ M M , M S , M E , S S , E S ] z \in[\mathrm{MM}, \mathrm{MS}, \mathrm{ME}, \mathrm{SS}, \mathrm{ES}] z∈[MM,MS,ME,SS,ES].
Inference Layer
Note that entity-to-entity (EE) edge is not pre-defined in the previous step. We can only generate EE edge representations by representing a path between their nodes. we adapt two-step inference mechanism to encode interactions between nodes and edges in the graph and hence model EE associations.
First Step
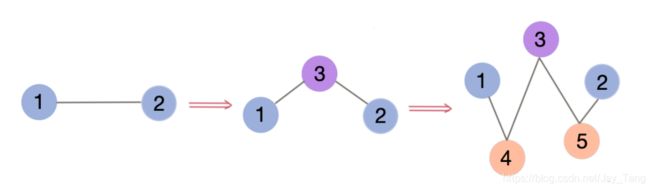
Goal: generate a path between two nodes i i i and j j j using intermediate nodes k k k (Intermediate nodes without adjacent edges to the target nodes are ignored).
We thus combine the representations of two consecutive edges e i k e_{ik} eik and e k j e_{kj} ekj, using a modified bilinear transformation. This action generates an edge representation of double length. We combine all existing paths between i i i and j j j through k k k:
f ( e i k ( l ) , e k j ( l ) ) = σ ( e i k ( l ) ⊙ ( W e k j ( l ) ) ) f\left(\mathbf{e}_{i k}^{(l)}, \mathbf{e}_{k j}^{(l)}\right)=\sigma\left(\mathbf{e}_{i k}^{(l)} \odot\left(\mathbf{W} \mathbf{e}_{k j}^{(l)}\right)\right) f(eik(l),ekj(l))=σ(eik(l)⊙(Wekj(l)))
where W ∈ \mathbf{W} \in W∈ R d z × d z \mathbb{R}^{d_{z} \times d_{z}} Rdz×dz is a learned parameter matrix, ⊙ \odot ⊙ refers to element-wise multiplication, l l l is the length of the edge and e i k \mathbf{e}_{i k} eik corresponds to the representation of the edge between nodes i i i and k k k.
Second Step
During the second step, we aggregate the original (short) edge representation and the new (longer) edge representation resulted from Equation (3) as follows: e i j ( 2 l ) = β e i j ( l ) + ( 1 − β ) ∑ k ≠ i , j f ( e i k ( l ) , e k j ( l ) ) \mathbf{e}_{i j}^{(2 l)}=\beta \mathbf{e}_{i j}^{(l)}+(1-\beta) \sum_{k \neq i, j} f\left(\mathbf{e}_{i k}^{(l)}, \mathbf{e}_{k j}^{(l)}\right) eij(2l)=βeij(l)+(1−β)k=i,j∑f(eik(l),ekj(l)) where β ∈ [ 0 , 1 ] \beta \in[0,1] β∈[0,1].
The two steps are repeated a finite number of times N.
- Everytime when going through step one, we find an intermediate node. With initial edge length equal to 1, the first iteration results in edges of length up-to 2. The second iteration results in edges of length up-to 4. Similarly, after N iterations, the length of edges will be upto 2 N 2^N 2N.Here is an illustration after iterations:
Classification Layer
We use the entity-to-entity edges (EE) of the document graph that correspond to the concept-level entity pairs to classify the concept-level entity pairs
y = softmax ( W c e E E + b c ) \mathbf{y}=\operatorname{softmax}\left(\mathbf{W}_{c} \mathbf{e}_{\mathrm{EE}}+\mathbf{b}_{c}\right) y=softmax(WceEE+bc) where W c ∈ R r × d z \mathbf{W}_{c} \in \mathbb{R}^{r \times d_{z}} Wc∈Rr×dz and b c ∈ R r \mathbf{b}_{c} \in \mathbb{R}^{r} bc∈Rr are learned parameters of the classification layer and r r r is the number of relation categories.
Result
Three models being compared:
- Edge-oriented Graph (EoG) refers to our main model with edges {MM, ME, MS, ES, SS}.
- The EoG (Full) setting refers to a model with a fully connected graph, where the graph nodes are all connected to each other, including E nodes.
- The EoG (NoInf) setting refers to a no inference model, where the iterative inference algorithm is ignored.
- The EoG (Sent) setting refers to a model that was trained on sentences instead of documents.
- Our model performs significantly better on intra- and inter-sentential pairs, even compared to most of the models with external knowledge.
- For the inter-sentence pairs, performance significantly drops with EoG(Full) and EoG(NoInf). The former might indicate the existence of certain reasoning paths that should be followed in order to relate entities residing in different sentences.
- The intra-sentence pairs substantially benefit from the document-level information.
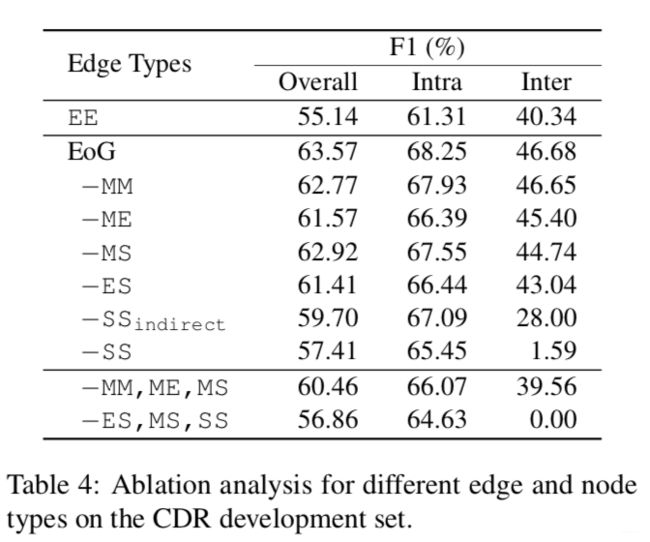
- Removal of ES edges reduces the performance of all pairs, as encoding of EE edges becomes more difficult and requires long inference paths as shown in figure (a). [we enable identification of pairs across sentences only through MM and ME edge. In this case, the minimum inference length is 6 (E-M-M-E-M-M-E)]

- As shown in figure (b), the introduction of S nodes results in a path with half the length, which we expect to better represent the relation.
- The figure above illustrates that for long-distanced pairs, EoG has lower performance, indicating a possible requirement for other latent document-level information.
Bad Cases Analysis
- The model cannot find associations between entities if they are connected by “and”.
- MIssing coreference connections.
- Incomplete entity linking.
Reference:
- Connecting the Dots: Document-level Neural Relation Extraction with Edge-oriented Graphs. https://arxiv.org/pdf/1909.00228.pdf.