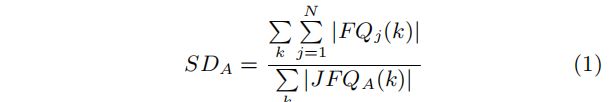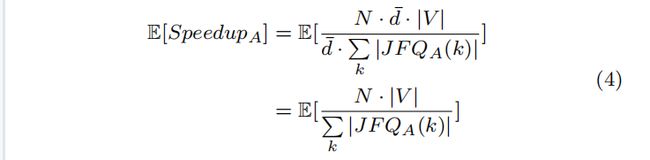【论文翻译】iBFS: Concurrent Breadth-First Search on GPUs
iBFS: Concurrent Breadth-First Search on GPUs
论文翻译,仅作为个人保存用
SIGMOD2016的文章,需要这篇原文可以私信我。
ABSTRACT
广度优先搜索(BFS)是一种具有许多重要应用价值的关键图算法。在这项工作中,我们关注一类特殊的图遍历算法——并发BFS,其中在同一图上同时执行多个宽度优先遍历。我们设计并开发了一种名为iBFS的新方法,它能够从i个不同的源顶点运行i个并发BFSes,这在图形处理单元(gpu)上非常有效。iBFS由三种新的设计组成。首先,iBFS开发了一个单一的GPU内核,用于联合遍历并发的BFS,以利用不同实例之间的共享边界。其次,基于出度的GroupBy规则使iBFS能够有选择地运行一组BFS实例,从而进一步最大化该组内的边界共享。第三,iBFS通过在GPU上使用高度优化的位操作带来额外的性能好处,这允许单个GPU线程检查并发BFS实例的顶点。对广泛的图形基准测试的评估表明,iBFS在一个GPU上比顺序执行BFS实例快30×,在112个GPU上实现了接近线性的加速
1.INTRODUCTION
基于图的表示在许多应用程序中无处不在,如社交网络、代谢网络和计算机网络。因此,图算法在大数据时代一直是一个重要的研究课题,其中广度优先搜索(BFS)由于其重要性而吸引了大量的兴趣。
在这项工作中,我们关注于一类特殊的BFS算法——并发BFS——其中在同一图上同时执行多个宽度优先遍历。我们将这个问题的解决方案称为iBFS,它能够在gpu上并行执行多个宽度优先遍历,每个gpu都来自一个不同的源顶点。这里i在1和|V |之间,即图中顶点的总数。
根据i的值,iBFS实际上变成了许多不同的问题。形式上,在带有|V |顶点的图中,iBFS是
如果i = 1 ,则为单源最短路径(SSSP);
如果i∈(1,|V |),则为多源最短路径(MSSP);
如果i = |V | ,则为全对最短路径(APSP)。
此外,iBFS还可以用于许多其他的图算法,如中间性中心性和接近中心性。例如,可以利用iBFS来构造回答图可达性查询的索引,即是否存在从顶点s到t的路径,其之间的边数小于k。我们将在本文中展示,这一步可以比iBFS更快一个数量级。总之,各种各样的应用程序,如网络路由、网络攻击检测、路由规划、web爬行等,都可以从高性能的iBFS中获益。
本文提出了一种在gpu上运行iBFS的新方法,该方法包括三种新技术:联合遍历、GroupBy和位向优化。之前的工作提出将不同BFS实例的执行主要结合在多核cpu上。然而,性能上的改进是有限的。首先,没有一个早期项目试图将BFS实例进行分组,以改进遍历期间的边界共享。此外,自下而上的BFS还提供了新的额外挑战。例如,虽然MS-BFS 支持自下而上,但它不提供iBFS利用以实现更快遍历的早期终止。本质上,BFS是一个内存密集型的工作负载,它与gpu提供的数千个轻量级线程很好地匹配。之前的工作,如[6,29-31],已经显示了在单源BFS中使用gpu的巨大成功。据我们所知,这是第一个在gpu上支持并发BFS的工作。
iBFS的第一种技术是由于观察到,一个简单地按顺序或并行运行多个BFS实例的简单实现将无法在gpu上实现高并行性。为了解决这一挑战,iBFS提出了联合遍历技术来利用不同并发BFS实例之间的共享边界,因为在我们已经评估过的一些图中,它们可以占高达48.6%的顶点。特别是,iBFS在单个GPU内核中执行不同的遍历。也就是说,所有并发的BFS实例都共享一个联合边界队列和一个联合状态数组。
其次,为了实现联合遍历的最大效益,iBFS应一起执行所有BFS实例。然而,由于有限的硬件资源,例如,gpu上的全局内存大小和线程计数,这是不可能的。幸运的是,我们发现可以对分组BFS实例进行优化,以确保不同实例之间的高边界共享比例。在群间共享比定理的指导下,iBFS开发了GroupBy的第二种技术,选择性地将BFS实例合并到优化的批次中,从而使整体性能加速2×。
一个典型的BFS算法以自上而下的方式从源顶点开始,检查每一层的边界,然后切换到自下而上,以避免不必要地检查过多的边。GroupBy在自上而下和自下而上两方面都提高了iBFS的性能,尽管改进的方式不同。在自上而下的操作中,更高的共享比率直接减少了用于检查和扩展的内存访问的数量。相比之下,通过共享,GroupBy允许自下而上的遍历在大致相同的时间内完成,最大限度地减少多个BFSes之间的工作负载不平衡。
第三,iBFS需要在多个级别上检查大量的边界,在某些情况下,比单个BFS多15个×。虽然对于每个单独的BFS,并不是每个顶点都是每个级别的边界,但并发的BFS显著增加了每个级别的边界数量。虽然gpu提供了数千个硬件线程,但并行地遍历大型图形的数百万个顶点仍然具有挑战性。为此,iBFS利用了一个位级状态数组,该数组使用一个位来表示每个BFS实例的顶点的状态。这减少了检查期间获取的数据的大小,更重要的是通过位操作减少了检查所需的线程数,一起加速图遍历11×。
综上所述,本文的贡献如下:
1.iBFS结合了联合遍历和GroupBy,允许自上而下和自下而上的BFS在每个组中非常有效地运行。这是通过使用一组基于出度的GroupBy规则来形成良好的并发BFS实例组来实现的,这些实例能够在它们之间享有较高的边界共享率。并对边界共享和分组共享进行了理论研究。
2.iBFS还开发了基于位操作的检查和边界识别,这进一步简化了对gpu的遍历,并提供了另一个关键的好处,即允许自下而上的BFS的早期终止。因此,与最先进的[26]相比,iBFS实现了高达2.6×的加速。
3.我们已经在广泛的图形上,以及在单个GPU和一个集群上实现和评估了iBFS。据我们所知,这是第一个在联合数据结构上运行基于gpu的并发BFS,即联合前沿队列和位状态数组,并以前所未有的遍历率扩展到O(100)gpu,即在112个gpu上每秒提供572670亿个遍历边(TEPS)。
本文的其余部分组织如下:第2节介绍了BFS的背景、并发BFS和动机。第4节介绍了单核和联合遍历的设计。第5节讨论了我们的分组技术。第6节介绍了按位进行的优化。第8节介绍了对我们的iBFS系统的评估。第9节讨论了相关工作,第10节总结。
2.BACKGROUND
BFS通常在自上而下的遍历,在稍后的[32,33]中切换到自下而上。这两个方向在每个级别上都执行三个任务,即扩展、检查和边界队列生成。首先,边界队列(FQ)将使用源顶点进行初始化,并将始终包含要在下一层中展开的顶点(边界)。从边界,展开探索它们的边到相邻顶点,检查更新状态数组(SA)中的邻居的状态,该状态数组为每个顶点维护记录(未访问、边界或访问)。
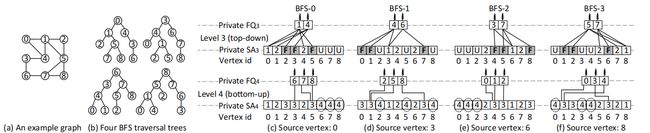
在自上而下的BFS中,扩展和检查的目的是识别每个边界的未访问的邻居。图1给出了一个宽度优先遍历的示例。给定图1(a)中的图,在第3级,图1©上半部分显示的一个自上而下的BFS(从顶点0开始的BFS-0)将从队列{1,4}展开,并将它们未访问的邻居{2,3,5}标记为状态数组中的边界。虽然之前已经访问过顶点{0,1,4},但它们仍然会在这个级别上进行检查,但是它们的状态将不会被更新。
图1: (a)本文使用的示例图(b)来自不同源顶点的四种有效BFS遍历树,分别为BFS-0、BFS-1、BFS-2和BFS-3,从顶点0、BFS 3、6和8开始。©、(d)、(e)和(f)是对应的四棵有效树的两个层次遍历在这里插入图片描述
,其中上半部分代表自上而下的遍历,下半部分代表自下而上。在所有的示例中,FQ和SA分别代表边界队列和状态数组。边界队列存储边界,状态数组表示当前级别中每个边界的状态,其中“F”、“U”和数字分别表示“边界”、“未访问”及其深度(已访问)。虚线圈表示每个边界的更新深度。
相反,自下而上的BFS会在展开和检查中尝试为未访问的顶点找到一个父节点,在这种情况下,它将在边界队列中存储未访问的顶点。在图1©的下半部分,第4级、{6、7、8}处的BFS-0是未访问的顶点,即在这里被视为边界。对于顶点6,由于它的第一个邻居3被访问,自下而上的BFS将把顶点6的深度标记为4,并且不需要检查额外的邻居。这就是我们所说的在自下而上的BFS中的早期终止,这可能会导致显著的性能提高。在iBFS中新提出的位优化可以进一步加快并发遍历的过程,并导致更高的性能。
在每个级别的三个任务中,检查边界的相邻顶点涉及到大量的随机内存访问(指针追逐),占了大部分的运行时间。这可以在图1中的自上而下和自下而上的四个BFS遍历上观察到。
并发的BFS从不同的源顶点执行多个BFS实例。使用图1中的示例,四个BFS实例分别从顶点0、3、6和8开始。并发BFS的简单实现将单独运行所有BFS实例,并保留其自己的私有边界队列和状态数组。在一个GPU设备上,每个单独的子例程都被定义为一个内核。因此,在前面的示例中,四个内核将从四个源顶点并行运行四个BFS实例。NVIDIA Kepler提供了Hyper-Q来支持多个内核的并发执行,这大大提高了GPU的利用率,特别是当单个内核不能充分利用GPU [34]时。
不幸的是,这种并发BFS的简单实现所花费的时间与顺序运行这些BFS实例大致相同,我们将在后面的第8节中展示。例如,对于本文中评估的所有图,并发BFS的顺序实现和朴素实现平均分别需要52个ms和48个ms,遍历率差异为5亿TEPS。这样一个小的好处的主要原因是,简单地并行运行多个BFS实例就会淹没GPU,特别是在一个BFS从自上而下到自下而上的方向转换级别上。此时,每个单独的BFS都将需要大量的线程来完成它们的工作负载。因此,这种幼稚的实现甚至可能不如所有BFS实例的顺序执行。
边界共享的机会: iBFS旨在通过利用不同BFS实例之间共享的边界的存在来解决这个问题。图2显示了两个实例之间每个级别的共享边界的平均百分比。本文中使用的图见第8节。自上而下级别的共享边界数量较少(平均接近4%),而自下而上级别的共享边界数量远高达48.6%。这是因为自底向上的遍历通常从大量未访问的顶点(在本例中是边界)开始,然后搜索它们的父节点。所提出的GroupBy技术可以将两个方向的共享率分别提高到10×和1.7×。
在并发的BFS中,共享的边界可能会产生三个好处: (1)。这些边界只需要进入边界队列一次。 (2).共享边界的邻居只需要在核心内加载一次。 (3).对不同BFSes的这些邻居的状态的内存访问可以被合并。需要注意的是,每个BFS仍然必须独立地检查状态,因为并不是所有的BFSes都将为它们的邻居具有相同的状态。换句话说,共享边界并不会减少总体工作量。然而,这项工作提出,共享边界可以用来提供更快的数据访问和节省内存使用,这两者对gpu都是至关重要的。这是通过逐位、联合遍历和GroupBy规则的组合来实现的,这些规则指导选择并行执行的BFSes组。
3. iBFS OVERVIEW
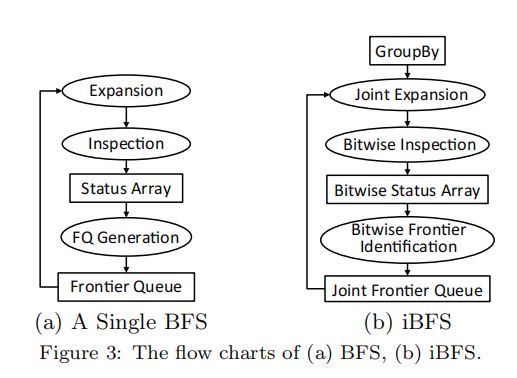
简而言之,如图3所示的iBFS由三种独特的技术组成,即联合遍历、GroupBy和位优化,它们将分别在第4、5和6节中讨论。
理想情况下,iBFS的最佳性能是通过运行所有BFS实例而没有GroupBy。不幸的是,不断增长的图形大小,再加上有限的GPU硬件资源,限制了并发BFS实例的数量。特别是,我们发现GPU全局内存是主导因素,例如,与许多TB规模的图相比,K40 GPU上有12GB。
设M为GPU内存大小,N为一个组中并发BFS实例的最大数量(即组大小)。如果整个图需要S存储,则单个BFS实例需要 ∣ S A ∣ |SA| ∣SA∣来存储其数据结构(例如,所有顶点的状态数组),而对于联合遍历,每个组对于联合数据结构(例如,联合边界队列)至少需要 ∣ J F Q ∣ \mid JFQ\mid ∣JFQ∣,然后是 N ≤ M − S − ∣ J F Q ∣ ∣ S A ∣ N\leq \frac{M−S−|JF Q|}{|SA|} N≤∣SA∣M−S−∣JFQ∣。在大多数情况下,N满足 1 < N ≪ i ≪ ∣ V ∣ 1 < N \ll i\ll|V | 1<N≪i≪∣V∣。在本文中,我们默认使用N的值为128。
不幸的是,随机分组N个不同的BFS实例不太可能产生最佳的性能。必须注意确保有一个良好的分组策略。为了说明这个问题,对于具有两个BFS实例BFS-s和BFS-t的A组,设 J F Q A ( k ) JF Q_A (k) JFQA(k)为A组在k级的联合边界队列, F Q s ( k ) F Q_s (k) FQs(k)为BFS-s的单个边界队列,BFS-t的 F Q t F Q_t FQt。因此, ∣ J F Q A ( k ) ∣ = ∣ F Q s ( k ) ∣ ∪ ∣ F Q t ( k ) ∣ − ∣ F Q s ( k ) ∣ ∩ ∣ F Q t ( k ) ∣ |JF Q_A (k)| = |F Q_s (k)|∪|F Q_t (k)|−|F Q_s (k)|∩|F Q_t (k)| ∣JFQA(k)∣=∣FQs(k)∣∪∣FQt(k)∣−∣FQs(k)∣∩∣FQt(k)∣,其中 ∣ F Q s ( k ) ∣ ∩ ∣ F Q t ( k ) ∣ |F Qs (k)|∩|F Qt (k)| ∣FQs(k)∣∩∣FQt(k)∣表示两个BFS实例之间的共享边界。显然,每个组拥有的共享前沿越多,iBFS就能够实现更高的性能。在我们在第5节中描述旨在最大化每个组内共享的GroupBy技术之前,我们将首先在下一节中介绍iBFS如何实现联合遍历,从而使并行执行成为可能。
4. JOINT TRAVERSAL
在这项工作中,我们建议在单个GPU内核中实现iBFS,不同于之前的基于GPU的工作[35]。通过这种方式,iBFS将能够利用不同BFS实例之间的共享,例如,如果同一内核的两个线程被计划在共享边界上工作,那么iBFS只需要从全局内存中加载相邻的顶点一次
。否则,这种好处将不可能实现于用于上述幼稚实现的多内核实现。
iBFS的联合遍历对所有并发的BFS实例使用两个联合数据结构:
(1)联合状态数组(JSA)用于保持所有实例的每个顶点的状态。对于每个顶点,iBFS依次放置不同的BFS实例的状态。例如,在图4中,当我们运行4个并发BFSes时,每个顶点使用4个字节。对于顶点0,第一个字节1表示顶点0的BFS-0的深度为1,接下来的三个字节表示相同的顶点0所有其他三个BFS实例还没访问它。
(2)联合边界队列(JFQ)是来自并发BFS实例的所有边界的集合,其中任何共享边界只出现一次。因此,这个队列需要|V |的最大大小来存储所有 i B F S i BFS iBFS实例的边界。相比之下,使用私有边界队列将需要一个更大的具有 i × ∣ V ∣ i×|V| i×∣V∣大小的队列。
一个GPU使用单指令多线程(SIMT)模型,并在一个由32个线程[36]组成的翘线中调度线程。一些扭曲可以形成一个称为协作线程数组(CTA)的线程块。块内的线程可以通过共享内存和内置原语进行快速通信。
为了生成JFQ,iBFS分配一个经线来扫描每个顶点的状态,如图4所示。如果这个顶点碰巧是任何BFS实例的边界,iBFS需要将其存储在联合边界队列中,例如,顶点1放在JFQ3中,因为它是级别3级BFS-0的边界。相比之下,顶点0并不被认为是所有四个BFS实例的边界。
值得注意的是,iBFS使用CUDA投票指令,即_ _any(),在同一扭曲中的不同线程之间进行通信,并调度一个线程来排队。此外,iBFS使用另一个CUDA特性__ballot(参数)来生成一个单独的变量来指示哪些BFS实例共享这个边界。这对于共享边界很重要,例如,当顶点7是BFS-2和BFS-3中的边界,它会在联合边界队列中出现一次。从队列中删除这些冗余边界将大大减少了昂贵的全局内存更新的数量,这在一定程度上有助于iBFS获得的性能提高。
iBFS的联合遍历引入了两种独特的内存优化,以减少昂贵的全局内存事务的数量:
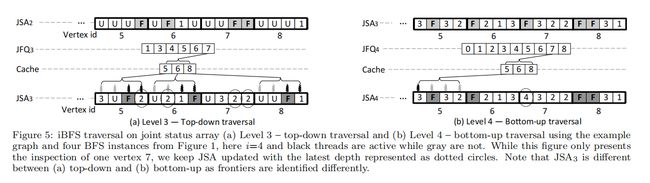
(1)在扩展期间,iBFS使用图5所示的新缓存来加载边界的相邻顶点,从GPU的全局内存到其共享内存,以满足所有BFS实例。这样,来自每个边界的邻居将只能从全局内存中加载一次,尽管许多请求可能来自多个BFS实例。这种好处不仅局限于共享的边界,而是队列中的每个边界。
2)在检查过程中,iBFS调度多个具有连续线程id的线程在每个边界上工作。这里的线程数与并发执行的BFS实例的数量相同。这是因为在gpu上,一个全局内存事务通常从一个数组中获取16个连续的数据条目,并且只有连续的线程才能共享检索到的数据。另一方面,如果连续的线程写入同一个内存块,这样的写入也会合并成一个全局内存事务。
现在,我们将使用一个示例来展示iBFS如何在自上而下和自下而上的遍历中利用这些新结构。图5(a)展示了顶点7的自顶向下的遍历,该顶点7是后续级别(即级别2)的一个边界。在扩展过程中,顶点7的邻居{5、6、8}被加载到缓存中。在检查过程中,没有此边界的BFS实例将不会检查邻居,特别是该图中的第一个和第二个线程。另一方面,当第三个和第四个线程访问三个邻居的状态时,它将在一个全局内存事务中执行,因为这些状态是并排存储的,并由连续的线程访问。在这个级别上,顶点7的状态也将更新为深度2。
自底向上的遍历以不同的方式执行,如图5(b).所示对于边界顶点7,iBFS将类似地将其相邻的顶点{5、6,8}加载到缓存中。这里的不同之处是,iBFS将检查{5,6,8}是否已经被访问过,如果是,请将7的深度标记为4。
请注意,一个顶点可以是自上而下和自底而上级别上的边界,例如,图5中的顶点7。在图5(a)中,顶点7是第三和第四个BFSes的自上而下遍历的边界,而在图5(b)中,第一个BFS的自下而上。显然,只要一个BFS将一个顶点视为一个特定级别上的边界,这个顶点就应该在iBFS中排队。
5. GROUPBY
在本节中,我们将介绍共享比率的概念,并提出几种基于出度的GroupBy规则。我们将首先使用自上而下的遍历来讨论GroupBy,然后介绍对自下而上的BFS的影响。
5.1边界共享程度和比例
在很大程度上,iBFS的性能取决于在每个组的联合遍历期间,在每个级别上共享了多少个边界。这是因为如果多个BFS实例在一个级别上有一个共同的边界,它的所有边界将只检查一次,从而提高整体性能。在本工作中,我们定义了任何组,如大小为N的组A,将共享度(SDA)定义为联合边界队列中存在的共享度:
其中, j ∈ [ 1 , N ] j∈[1,N] j∈[1,N]和表示A组中的第j个BFS实例,k表示遍历的级别(或深度)。本质上, S D A SD_A SDA显示每个联合边界平均由组中多少BFS实例共享。因此,共享比率可以很容易地计算为SD除以组中的实例总数
传统上,BFS的时间复杂度是通过执行的检查次数来计算的,即边缘计数|E|。因此,a组顺序执行的时间将为N·|E|。
在这项工作中,我们使用 T A ( k ) T_A (k) TA(k)来表示A组在k级上联合执行的时间,即,
T A ( k ) = ∑ v ∈ J F Q A ( k ) o u t d e g r e e ( v ) T_A (k) = \sum_{v∈JF Q_A (k)} outdegree (v) TA(k)=∑v∈JFQA(k)outdegree(v) (1)
其中,v代表JFQ中k级的每个边界。通过汇总各级别的运行时,可以计算出A组的总运行时TA,即:
T A = ∑ k T A ( k ) = ∑ k ∑ v ∈ J F Q A ( k ) o u t d e g r e e ( v ) ) T_A = \sum_ k T_A (k) = \sum_k \sum _{v∈JF Q_A (k)} outdegree (v) ) TA=∑kTA(k)=∑k∑v∈JFQA(k)outdegree(v)) (2)
根据Amdahl定律,A组的联合遍历超过顺序执行的加速速度为:
S p e e d u p A = N ⋅ ∣ E ∣ T A Speedup_A=\frac {N·\mid E\mid}{ T_A} SpeedupA=TAN⋅∣E∣ (3)
设d¯为平均出度,我们可以利用方程(2)和(3)得到 S p e e d u p A Speedup_A SpeedupA的期望值。因此
引理1。对于任何BFS组,如A组,其共享比等于 S p e e d u p A Speedup_A SpeedupA的期望值,即,
S D A = E [ S p e e d u p A ] SDA = E[Speedup_A] SDA=E[SpeedupA] (5)
证明。因为对于第j个BFS,每个顶点将在其中一个层次上成为边界,所有级别的 ∣ F Q j ( k ) ∣ |F Q_j (k)| ∣FQj(k)∣的总和等于顶点的总数,即 ∑ k ∣ F Q j ( k ) ∣ = ∣ V ∣ \sum_ k |F Q_j (k)| = |V | ∑k∣FQj(k)∣=∣V∣。
引理1表明,当它与该组的顺序执行相比时,共享比率反映了联合执行的性能。但是,对于任何一组,由于每个级别的JFQ的大小直到运行时才知道,因此我们将无法先验计算共享比率和预期性能。幸运的是,我们发现在前几个水平上的共享比率可以作为一个很好的度量标准,并且在连续水平上的共享比率也存在一个重要的相关性。
定理1。给定具有相同数量BFS实例的BFS组A和B,如果在k级,它们的共享比率服从 S D A ( k ) > S D B ( k ) SD_A (k) > SD_B (k) SDA(k)>SDB(k),在k + 1级,以下关系 E [ S D A ( k + 1 ) ] > E [ S D B ( k + 1 ) ] E[SD_A(k+1)]>E[SD_B(k+1)] E[SDA(k+1)]>E[SDB(k+1)]将成立。
证明。让我们从一组a开始。在k级,第j个BFS对一个边界顶点v执行两个主要任务,即展开和检查。在第一个任务中,第j个BFS获取边界v的邻居列表,在第二个任务中,它检查所有的邻居。检查的次数等于v。
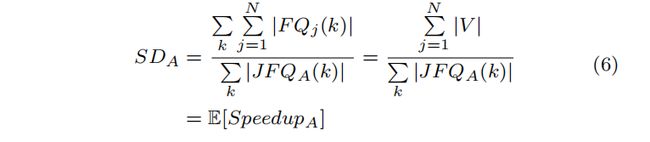
我们将空检查定义为那些不会导致特定级别上边界队列大小增加的检查。请注意,由于顶点是共享的,因此空检查并不一定意味着这些检查在下一层没有找到边界。有三种情况可以将邻居检查呈现为空检查。前两种情况与单一BFS相关,而这三种情况都适用于iBFS。对于边境v的邻居w,
案例1:已访问的邻居w。
案例2:邻居w已经被k级的其他检查标记为一个新的边界。此检查将被丢弃,并且不会增加边界队列的大小。这是因为w可能有除v之外的其他父母。
案例3:邻居w已经被其他并发的BFS实例标记为一个新的边界。类似地,在联合遍历中,此检查将被丢弃,并且不会增加边界队列的大小,因为w可能会被并发的BFS实例共享。
我们使用三个值来表示三种情况的发生百分比:α代表单一BFS的病例1和病例2,β代表病例1和iBFS的病例2,γ代表iBFS单独的病例3。因此,单个BFS的情况1和情况2的补数的概率可以用(1−α)来表示,以此类推。
看不懂了啊,崩溃了,不写了