利用传输矩阵法求解布拉格光栅的透射谱
利用传输矩阵法求解布拉格光栅的透射谱
采用传输矩阵法(TMM)计算具有任意折射率分布光栅结构的透射谱,TMM法描述如下:
- 能够计算折射率呈阶梯状分布的波导的反射和透射率,以及波导的传播常数。
- 在单模波导中,计算反射和透射率采用2×2的矩阵表示。
- 为了表示光栅(多个折射率突变界面),将矩阵乘成级联网络,
- 能够计算光栅针对每个波长的透射值和反射值。
1、均匀波导的传输矩阵
传输矩阵定义如下:
[ A 1 B 1 ] = [ T 11 T 12 T 11 T 12 ] [ A 2 B 2 ] \left[ \begin{matrix} A_1 \\ B_1 \\ \end{matrix}\right] = \left[ \begin{matrix} T_{11} & T_{12} \\ T_{11} & T_{12} \\ \end{matrix}\right] \left[ \begin{matrix} A_2 \\ B_2 \\ \end{matrix}\right] [A1B1]=[T11T11T12T12][A2B2]

传递矩阵的概念类似于散射参数矩阵,波导的均匀截面如图(a)所示的传输矩阵如下:
T h w = [ e j β L 0 0 e − j β L ] T_{hw}= \left[ \begin{matrix} e^{j\beta L} & 0 \\ 0 & e^{-j\beta L} \\ \end{matrix}\right] Thw=[ejβL00e−jβL]
其中,β为场的复传播常数,包括折射率和传播损耗:
β = 2 π n e f f λ − i α 2 \beta = \frac{2\pi n_{eff}}{\lambda}-i\frac{\alpha}{2} β=λ2πneff−i2α
计算均匀波导的传输矩阵法其MATLAB代码如下:
function T_hw=TMM_HomoWG_Matrix(wavelength,l,neff,loss)
% Calculate the transfer matrix of a homogeneous waveguide.
% Complex propagation constant
beta=2*pi*neff./wavelength-1i*loss/2;
T_hw=zeros(2,2,length(neff));
T_hw(1,1,:)=exp(1i*beta*l);
T_hw(2,2,:)=exp(-1i*beta*l);
2、折射率呈阶梯状分布的波导
折射率呈阶梯状分布的波导的传递矩阵,如图b所示,为
T i s − 12 = [ 1 / t r / t r / t 1 / t ] = [ n 1 + n 2 2 n 1 n 2 n 1 − n 2 2 n 1 n 2 n 1 − n 2 2 n 1 n 2 n 1 + n 2 2 n 1 n 2 ] T_{is-12}= \left[ \begin{matrix} 1/t & r/t \\ r/t & 1/t \\ \end{matrix}\right]= \left[ \begin{matrix} \frac{n_1+n_2}{2\sqrt{n_1 n_2}} & \frac{n_1-n_2}{2\sqrt{n_1 n_2}} \\ \frac{n_1-n_2}{2\sqrt{n_1 n_2}} & \frac{n_1+n_2}{2\sqrt{n_1 n_2}} \\ \end{matrix}\right] Tis−12=[1/tr/tr/t1/t]=[2n1n2n1+n22n1n2n1−n22n1n2n1−n22n1n2n1+n2]
其中r和t是基于菲涅耳系数的反射率和透射率。计算折射率呈阶梯状分布的波导界面的传输矩阵的MATLAB代码如下:
function T_is=TMM_IndexStep_Matrix(n1,n2)
% Calculate the transfer matrix for a index step from n1 to n2.
T_is=zeros(2,2,length(n1));
a=(n1+n2)./(2*sqrt(n1.*n2));
b=(n1-n2)./(2*sqrt(n1.*n2));
%T_is=[a b; b a];
T_is(1,1,:)=a; T_is(1,2,:)=b;
T_is(2,1,:)=b; T_is(2,2,:)=a;
3、布拉格光栅及反射和透射率
表述布拉格光栅的级联矩阵如下:
T p = T t w − 2 T i s − 21 T h w − 1 T i s − 12 T_p=T_{tw-2}T_{is-21}T_{hw-1}T_{is-12} Tp=Ttw−2Tis−21Thw−1Tis−12
其中下标1和2表示低和高折射率的区域。然后构造有N个周期的均匀布拉格光栅:
T p = ( T t w − 2 T i s − 21 T h w − 1 T i s − 12 ) N T_p=(T_{tw-2}T_{is-21}T_{hw-1}T_{is-12})^N Tp=(Ttw−2Tis−21Thw−1Tis−12)N
考虑了相移均匀布拉格光栅,即带有两个布拉格光栅反射器的一级FP腔,传递矩阵如下:
T = [ ( T p ) N ] T h w − 2 [ ( T p ) N ] T h w − 2 T=[(T_p)^N]T_{hw-2}[(T_p)^N]T_{hw-2} T=[(Tp)N]Thw−2[(Tp)N]Thw−2
计算由波导截面和材料界面组成的波导布拉格光栅腔的传输矩阵MATLAB代码如下:
function T=TMM_Grating_Matrix(wavelength, Period, NG, n1, n2, loss)
% Calculate the total transfer matrix of the gratings
l=Period/2;
T_hw1=TMM_HomoWG_Matrix(wavelength,l,n1,loss);
T_is12=TMM_IndexStep_Matrix(n1,n2);
T_hw2=TMM_HomoWG_Matrix(wavelength,l,n2,loss);
T_is21=TMM_IndexStep_Matrix(n2,n1);
q=length(wavelength);
Tp=zeros(2,2,q); T=Tp;
for i=1:length(wavelength)
Tp(:,:,i)=T_hw2(:,:,i)*T_is21(:,:,i)*T_hw1(:,:,i)*T_is12(:,:,i);
T(:,:,i)=Tp(:,:,i)^NG; % 1st order uniform Bragg grating
% for an FP cavity, 1st order cavity, insert a high index region, n2.
T(:,:,i)=Tp(:,:,i)^NG * (T_hw2(:,:,i))^1 * Tp(:,:,i)^NG * T_hw2(:,:,i);
end
我们将光栅以折射率为n2的部分作为开始和结束。相移区域是采用高折射率材料n2来实现的。最后,生成透射T和反射R谱。通过对波长点的一维矩阵进行了计算。计算光栅的反射和透射率MATLAB代码如下:
function [R,T]=TMM_Grating_RT(wavelength, Period, NG, n1, n2, loss)
%Calculate the R and T versus wavelength
M=TMM_Grating_Matrix(wavelength, Period, NG, n1, n2, loss);
q=length(wavelength);
T=abs(ones(q,1)./squeeze(M(1,1,:))).^2;
R=abs(squeeze(M(2,1,:))./squeeze(M(1,1,:))).^2;
4、光栅物理结构设计
接下来将物理结构(波导几何形状)与有效折射率联系起来。输出波导部分为500×220 nm的条形波导和氧化物包层组成,其中波导宽度发生变化构成了光栅。
使用本征模计算光栅段的有效折射率,通过计算了波导与波长和波导宽度之间的有效折射率,然后对其进行参数化。数据可以通过曲线拟合为两个函数:
n e f f − λ ( λ ) = a 0 − a 1 ( λ − λ 0 ) − a 2 ( λ − λ 0 ) 2 n e f f − w ( w ) = a 0 − a 1 ( w − w 0 ) − a 2 ( w − w 0 ) 2 n_{eff-\lambda}(\lambda)=a_0-a_1(\lambda-\lambda_0)-a_2(\lambda-\lambda_0)^2\\ n_{eff-w}(w)=a_0-a_1(w-w_0)-a_2(w-w_0)^2 neff−λ(λ)=a0−a1(λ−λ0)−a2(λ−λ0)2neff−w(w)=a0−a1(w−w0)−a2(w−w0)2
其中,lambda的单位值微米,w为µm中的波导的宽度,neff (w)为给定波导宽度w下的有效折射率相对于其在λ0处的值的偏差。
定义光栅的物理参数,并画出频谱的MATLAB代码:
function Grating
%This file is used to plot the reflection/transmission spectrum.
% Grating Parameters
Period=310e-9; % Bragg period
NG=200; % Number of grating periods
L=NG*Period; % Grating length
width0=0.5; % mean waveguide width
dwidth=0.01; % +/- waveguide width
width1=width0 - dwidth;
width2=width0 + dwidth;
loss_dBcm=3; % waveguide loss, dB/cm
loss=log(10)*loss_dBcm/10*100;
% Simulation Parameters:
span=30e-9; % Set the wavelength span for the simultion
Npoints = 10000;
% from MODE calculations
switch 1
case 1 % Strip waveguide; 500x220 nm
neff_wavelength = @(w) 2.4379 - 1.1193 * (w*1e6-1.554) - 0.0350 * (w*1e6-1.554).^2;
% 500x220 oxide strip waveguide
dneff_width = @(w) 10.4285*(w-0.5).^3 - 5.2487*(w-0.5).^2 + 1.6142*(w-0.5);
end
% Find Bragg wavelength using lambda_Bragg = Period * 2neff(lambda_bragg);
% Assume neff is for the average waveguide width.
f = @(lambda) lambda - Period*2*(neff_wavelength(lambda)+(dneff_width(width2)+dneff_width(width1))/2);
wavelength0 = fzero(f,1550e-9);
wavelengths=wavelength0 + linspace(-span/2, span/2, Npoints);
n1=neff_wavelength(wavelengths)+dneff_width(width1); % low index
n2=neff_wavelength(wavelengths)+dneff_width(width2); % high index
[R,T]=TMM_Grating_RT(wavelengths, Period, NG, n1, n2, loss);
figure;
plot (wavelengths*1e6,[R, T],'LineWidth',3); hold all
plot ([wavelength0, wavelength0]*1e6, [0,1],'--'); % calculated bragg wavelength
xlabel('Wavelength [\mum]')
ylabel('Response');
axis tight;
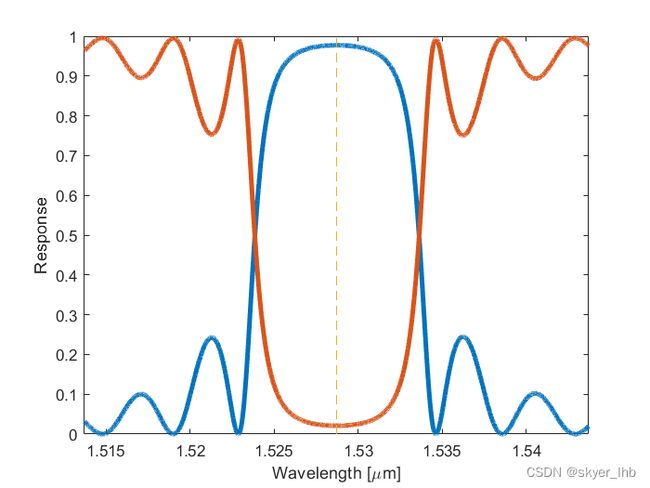
计算结果如下图所示:
5、Lumerical求解
通过Lumerial的FDTD求解光栅透射率代码如下:
###############################################
# script file: Bragg_FDTD.lsf
#
# Create and simulate a basic Bragg grating
# Copyright 2014 Lumerical Solutions
###############################################
# DESIGN PARAMETERS
###############################################
thick_Si = 0.22e-6;
thick_BOX = 2e-6;
width_ridge = 0.5e-6; # Waveguide width
Delta_W = 50e-9; # Corrugation width
L_pd = 324e-9; # Grating period
N_gt = 280; # Number of grating periods
L_gt = N_gt*L_pd;# Grating length
W_ox = 3e-6; L_ex = 5e-6; # simulation size margins
L_total = L_gt+2*L_ex;
material_Si = ’Si (Silicon) - Dispersive & Lossless’;
material_BOX = ’SiO2 (Glass) - Const’;
# Constant index materials lead to more stable simulations
# DRAW
###############################################
newproject; switchtolayout;
materials;
# Oxide Substrate
addrect;
set(’x min’,-L_ex); set(’x max’,L_gt+L_ex);
set(’y’,0e-6); set(’y span’,W_ox);
set(’z min’,-thick_BOX); set(’z max’,-thick_Si/2);
set(’material’,material_BOX);
set(’name’,’oxide’);
# Input Waveguide
addrect;
set(’x min’,-L_ex); set(’x max’,0);
set(’y’,0); set(’y span’,width_ridge);
set(’z’,0); set(’z span’,thick_Si);
set(’material’,material_Si);
set(’name’,’input_wg’);
# Bragg Gratings
addrect;
set(’x min’,0); set(’x max’,L_pd/2);
set(’y’,0); set(’y span’,width_ridge+Delta_W);
set(’z’,0); set(’z span’,thick_Si);
set(’material’,material_Si);
set(’name’,’grt_big’);
addrect;
set(’x min’,L_pd/2); set(’x max’,L_pd);
set(’y’,0); set(’y span’,width_ridge-Delta_W);
set(’z’,0); set(’z span’,thick_Si);
set(’material’,material_Si);
set(’name’,’grt_small’);
selectpartial(’grt’);
addtogroup(’grt_cell’);
select(’grt_cell’);
redrawoff;
for (i=1:N_gt-1) {
copy(L_pd);
}
selectpartial(’grt_cell’);
addtogroup(’bragg’);
redrawon;
# Output WG
addrect;
set(’x min’,L_gt); set(’x max’,L_gt+L_ex);
set(’y’,0); set(’y span’,width_ridge);
set(’z’,0); set(’z span’,thick_Si);
set(’material’,material_Si);
set(’name’,’output_wg’);
# SIMULATION SETUP
###############################################
lambda_min = 1.5e-6;
lambda_max = 1.6e-6;
freq_points = 101;
sim_time = 6000e-15;
Mesh_level = 2;
mesh_override_dx = 40.5e-9; # needs to be an integer multiple of the period
mesh_override_dy = 50e-9;
mesh_override_dz = 20e-9;
# FDTD
addfdtd;
set(’dimension’,’3D’);
set(’simulation time’,sim_time);
set(’x min’,-L_ex+1e-6); set(’x max’,L_gt+L_ex-1e-6);
158 Fundamental building blocks
set(’y’, 0e-6); set(’y span’,2e-6);
set(’z’,0); set(’z span’,1.8e-6);
set(’mesh accuracy’,Mesh_level);
set(’x min bc’,’PML’); set(’x max bc’,’PML’);
set(’y min bc’,’PML’); set(’y max bc’,’PML’);
set(’z min bc’,’PML’); set(’z max bc’,’PML’);
#add symmetry planes to reduce the simulation time
#set(’y min bc’,’Anti-Symmetric’); set(’force symmetric y mesh’, 1);
# Mesh Override
if (1){
addmesh;
set(’x min’,0e-6); set(’x max’,L_gt);
set(’y’,0); set(’y span’,width_ridge+Delta_W);
set(’z’,0); set(’z span’,thick_Si+2*mesh_override_dz);
set(’dx’,mesh_override_dx);
set(’dy’,mesh_override_dy);
set(’dz’,mesh_override_dz);
}
# MODE Source
addmode;
set(’injection axis’,’x-axis’);
set(’mode selection’,’fundamental mode’);
set(’x’,-2e-6);
set(’y’,0); set(’y span’,2.5e-6);
set(’z’,0); set(’z span’,2e-6);
set(’wavelength start’,lambda_min);
set(’wavelength stop’,lambda_max);
# Time Monitors
addtime;
set(’name’,’tmonitor_r’);
set(’monitor type’,’point’);
set(’x’,-3e-6); set(’y’,0); set(’z’,0);
addtime;
set(’name’,’tmonitor_m’);
set(’monitor type’,’point’);
set(’x’,L_gt/2); set(’y’,0); set(’z’,0);
addtime;
set(’name’,’tmonitor_t’);
set(’monitor type’,’point’);
set(’x’,L_gt+3e-6); set(’y’,0); set(’z’,0);
# Frequency Monitors
addpower;
set(’name’,’t’);
set(’monitor type’,’2D X-normal’);
set(’x’,L_gt+2.5e-6);
set(’y’,0); set(’y span’,2.5e-6);
set(’z’,0); set(’z span’,2e-6);
set(’override global monitor settings’,1);
set(’use source limits’,1);
set(’use linear wavelength spacing’,1);
set(’frequency points’,freq_points);
addpower;
set(’name’,’r’);
set(’monitor type’,’2D X-normal’);
set(’x’,-2.5e-6);
set(’y’,0); set(’y span’,2.5e-6);
set(’z’,0); set(’z span’,2e-6);
set(’override global monitor settings’,1);
set(’use source limits’,1);
set(’use linear wavelength spacing’,1);
set(’frequency points’,freq_points);
#Top-view electric field profile
if (0) {addprofile;
References 159
set(’name’,’field’);
set(’monitor type’,’2D Z-normal’);
set(’x min’,-2e-6); set(’x max’,L_gt+2e-6);
set(’y’, 0); set(’y span’,1.2e-6);
set(’z’, 0);
set(’override global monitor settings’,1);
set(’use source limits’,1);
set(’use linear wavelength spacing’,1);
set(’frequency points’,21);
}
# SAVE AND RUN
###############################################
save(’Bragg_FDTD’);
run;
# Analysis
###############################################
transmission_sim=transmission(’t’);
reflection_sim=transmission(’r’);
wavelength_sim=3e8/getdata(’t’,’f’);
plot(wavelength_sim*1e9, 10*log10(transmission_sim),10*log10(abs(reflection_sim)),’wavelength (nm)’, ’response’);
legend(’T’,’R’);
matlabsave(’Bragg_FDTD’);