leetcode动态规划总结
leetcode动态规划总结
- 动态规划理论
- 一、解题步骤
- 二、动态规划如何debug
- 三、经典题目
-
- leetcode509.斐波那契数组
- leetcode70.爬楼梯
- leetcode746.使用最小花费爬楼梯
- leetcode62.不同路径
- leetcode63.不同路径2
- leetcode343.整数拆分
- leetcode96.不同的二叉搜索树
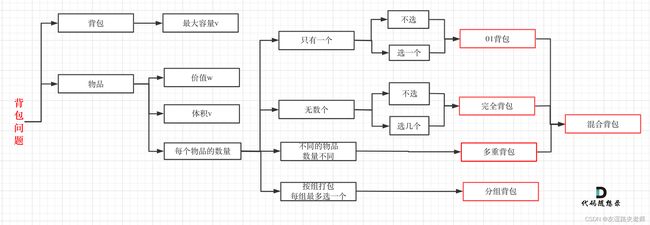
- 四、背包问题
-
- 4.1.01背包问题
动态规划理论
提示:文章内容来源于代码随想录,个人总结记录方便自己记忆:
动态规划(DP),某一问题存在很多重叠子问题,用dp一般有效。
记住动态规划每个状态从上一个状态推导而来即可。
一、解题步骤
五部曲:
(1)确定dp数组(dp table)以及下标的含义
(2)确定递推公式
(3)dp数组如何初始化
(4)确定遍历顺序
(5)举例推导dp数组
二、动态规划如何debug
(1)打印出dp数组,看看跟推导符不符合
(2)自己举例子模拟一遍
(3)重在推导
三、经典题目
leetcode509.斐波那契数组
这题转移方程给出来了,唯一需要注意的是n<2的时候需要列一下。
class Solution:
def fib(self, n: int) -> int:
if n < 2:
return n
dp = [0] * (n + 1)
dp[0] = 0
dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
用五部曲来简单列一下这道题的过程
(1)确定dp数组(dp table)以及下标的含义:
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
(2)确定递推公式:
题目给出了dp[i] = dp[i - 1] + dp[i - 2]
(3)dp数组如何初始化:
dp[0] = 0;
dp[1] = 1;
(4)确定遍历顺序
从公式可以看出顺序从前到后
(5)举例推导dp公式
N = 10代入,手写出dp数组,然后代码打印一遍,看看匹不匹配
leetcode70.爬楼梯
class Solution:
def climbStairs(self, n: int) -> int:
dp = [0] * (n + 1)
dp[0] = dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
leetcode746.使用最小花费爬楼梯
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
dp = [0] * (len(cost) + 1)
# 1.dp数组的意义
# dp[i]表示爬到第i楼需要的花费
# 2.dp数组的推导
# dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
# 3.dp数组的初始化
# dp[0] = 0
# dp[1] = 0
dp[0] = 0
dp[1] = 0
for i in range(2, len(cost) + 1):
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
return dp[len(cost)]
leetcode62.不同路径
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
# 1.确定dp数组意义
dp = [[1 for i in range(n)] for j in range(m)]
# 初始化
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1]
leetcode63.不同路径2
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
# 构造一个DP table
row = len(obstacleGrid)
col = len(obstacleGrid[0])
dp = [[0 for _ in range(col)] for _ in range(row)]
dp[0][0] = 1 if obstacleGrid[0][0] != 1 else 0
if dp[0][0] == 0: return 0 # 如果第一个格子就是障碍,return 0
# 第一行
for i in range(1, col):
if obstacleGrid[0][i] != 1:
dp[0][i] = dp[0][i-1]
# 第一列
for i in range(1, row):
if obstacleGrid[i][0] != 1:
dp[i][0] = dp[i-1][0]
print(dp)
for i in range(1, row):
for j in range(1, col):
if obstacleGrid[i][j] != 1:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[-1][-1]
leetcode343.整数拆分
class Solution:
def integerBreak(self, n: int) -> int:
dp = [0] * (n + 1)
dp[2] = 1
for i in range(3, n + 1):
for j in range(1, i - 1):
dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]))
return dp[n]
leetcode96.不同的二叉搜索树
这道题感觉挺有难度的
class Solution:
def numTrees(self, n: int) -> int:
dp = [0] * (n + 1)
dp[0], dp[1] = 1, 1
for i in range(2, n + 1):
for j in range(1, i + 1):
dp[i] += dp[j - 1] * dp[i - j]
return dp[-1]
四、背包问题
4.1.01背包问题
五部曲:
(1)确定dp数组以及下标的含义:对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
(2)确定递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
(3)初始化:这个是01背包问题的重点,先初始化dp[i][0],然后初始化dp[0][j],很好理解的是如果j=0即背包容量为0,那么dp[i][0]=0,当j>=weight[0]时,dp[0][j]初始化为value[0]。
(4)确定遍历顺序:一般是先物品后背包重量
(5)举例推导