形式语言与自动机 04 Regular Expressions

Regular Expressions

Definition

RE’ s: Introduction

• Regular expressions describe languages by an algebra
• They describe exactly the regular languages
• If E is a regular expression, then L(E) is the language it defines
• We’ll describe RE’ s and their languages recursively

Operations on Languages

Union

$\{01,111,10\}\cup \{00,01\}=\{01,111,10,00\}$

Concatenation

• The concatenation of languages $L$ and $M$ is denoted $LM$
• It contains every string $wx$ such that $w$ is in $L$ and $x$ is in $M$

$\{01,111,10\}\{00,01\}=\{0100,0101,11100,11101,1000,1001\}$

Kleene Star

• $L^{\ast }=\{ϵ\}\cup L\cup LL\cup LLL...\}$

$\{0,10{\}}^{\ast }=ϵ\cup \{0,10,00,010,100,1010,...\}$

RE’ s Definition

• Basis 1: If $a$ is any symbol. then $a$ is a RE, and L($a$) = {a}

  • Note: {a} is the language containing one string, and that string is of length 1

• Basic 2: $ϵ$ is a RE, and L($ϵ$) = {$ϵ$}

• Basic 3: $\varnothing$ is a RE, and L($\varnothing$) = $\varnothing$

• Induction 1: If $E_1$ and $E_2$ are regular expressions, then $E_1+E_2$ is a regular expression, and L($E_1+E_2$) = L($E_1$) + L($E_2$)

• Induction 2: If $E_1$ and $E_2$ are regular expressions, then $E_1{E}_2$ is a regular expression, and L($E_1{E}_2$) = L($E_1$)L($E_2$)

• Induction 3: If $E$ is a $RE$, then $E^{\ast }$ is a $RE$, and L($E^{\ast }$) = (L($E$))${}^{\ast }$

Precedence of Operators

• L(01) = {01}
• L(01+0) = {01,0}
• L(0(1+0)) = {01,00}
• L($0^{\ast }$) = {$ϵ,0,00,000,...$}
• L((0+10)${}^{\ast }$ ($ϵ$ + 1)) = all strings of 0’ s and 1’ s without two consecutive 1’ s

Equivalence to Finite Automata

We need to show that for every RE, there is a finite automaton that accepts

And for every finite automaton, there is a RE defining its language

Converting a RE to an $ϵ$-NFA

• Proof is an induction on the number of operators(+,concatenation,*) in RE

Basic

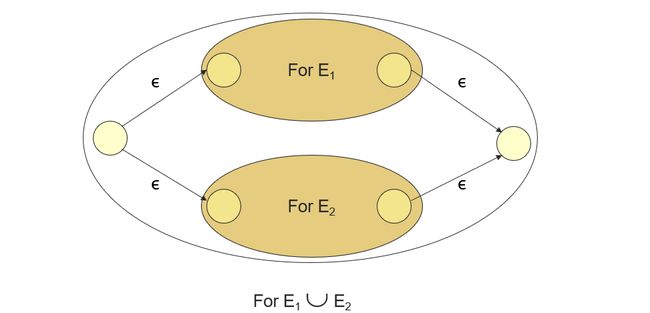
Union

Concatenation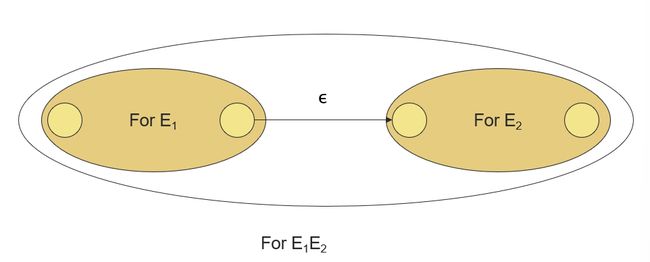

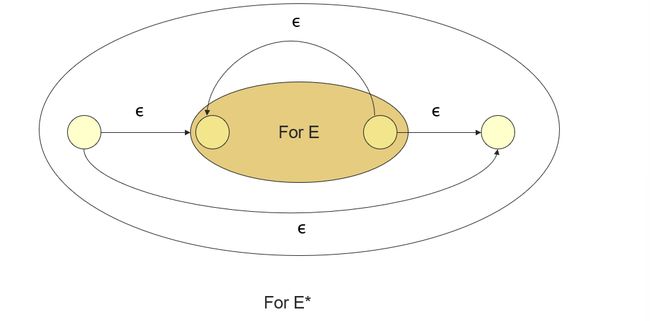
Closure

DFA to RE

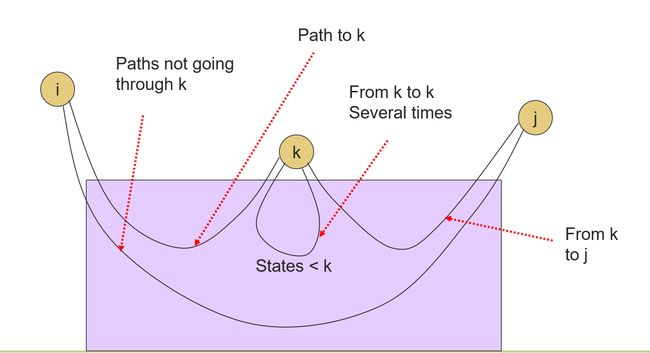
k-Paths

• A k-path is a path through the graph of the DFA that goes through no state numbered higher than k
• n-paths are unrestricted

RE is the union of RE’ s for the n-paths from the start state to each final state

• **Basis: ** k=0; only arcs or a node by itself
• **Induction: ** construct RE’ s for paths allowed to pass through state k from paths allowed only up to k-1

k-Path Induction

• Let $R_{ij}^k$ be the regular expression for the set of labels of k-paths from state i to state j
• Basis: k=0. $R_{ij}^0$ = sum of labels of arc from i to j
  • $\varnothing$ if no such arc
  • But add $\in$ if i=j

k-Path Inductive Case

$R_{ij}^k=R_{ij}^{k-1}+R_{ik}^{k-1}(R_{kk}^{k-1}{)}^{\ast }{R}_{kj}^{k-1}$

Final Step

• The RE with the same language as the DFA is the sum (union) of $R_{ij}^n,$ where:
  1. n is the number of states; i.e., paths are unconstrained
  2. i is the start state
  3. j is one of the final states

Summary

Each of the three types of automata (DFA,NFA,$ϵ$-NFA) we discussed, and regular expressions as well, define exactly the same set of languages: the regular languages

Algebraic Laws for RE’ s

Identities and Annihilators

• $\varnothing$ is the identity for +
  • R + $\varnothing$ = R
• $ϵ$ is the identity for concatenation
  • $ϵR=Rϵ=R$
• $\varnothing$ is the annihilator for concatenation
  • $\varnothing R=R\varnothing =\varnothing$

Decision Properties of Regular Languages

General Discussion of “Properties”

Properties of Language Classes

• A language class is a set of languages
• Language classes have two important kinds of properties
  • Decision properties
  • Closure properties

Closure Properties

A closure property of a language class says that given languages in the class, an operation(e.g) produces another language in the same class

example: the regular language are closed under union, concatenation and Kleene closure

Representation of Languages

formal or informal

Decision Properties

• A decision property for a class of languages corresponds an algorithm that takes a formal description of a language and tell whether or not some property holds
• Example: Is language L empty

Why Decision Properties

We might want a “smallest” representation for a language, a minimum-state DFA or a shortest RE

The Emptiness Problem

The Infiniteness Problem

• Is a given regular language infinite?

• **Key idea: ** if the DFA has n states, and the language contains any string of length n or more, then the language is inifinite

• Otherwise the language is surely finite

• **Second key idea: ** if there is a string of length $\ge$ n (= number of states) in L, then there is a string of length between n and 2n - 1

Proof

• Test for membership all strings of length between n and 2n -1
  • If any are accepted, then infinite, else finite
• A terrible algorithm
• **Better: ** find cycles between the start state and a final state

Finding Cycles

1. Eliminate states not reachable from the start state
2. Eliminate states that do not reach a final state
3. Test if then remaining transition graph has any cycle

The Pumping Lemma

泵引理

Statement of the Pumping Lemma

For every regular language L,

​ There is an integer n, such that

​ For every string w in L of length $\ge$ n

​ We can write w = xyz such that:

1. |xy| $\le$ n
2. |y| > 0
3. For all i $\ge$ 0, xy${}^i$z is in L

Example: Use of Pumping Lemma

泵引理帮助我们判断一些无穷语言是否为正则语言

$\{0^n{1}^n|k\ge 1\}$ is not a regular language

Proof

• Let w = $0^n{1}^n$, then write x = xyz, and y consists of 0’ s, y $\ne ϵ$

• But xyyz would be in L ,thus impossible

Decision Property： Equivalence

DFA L and M

• Let these DFA has sets of states Q and R

• Product DFA has set of states Q x R

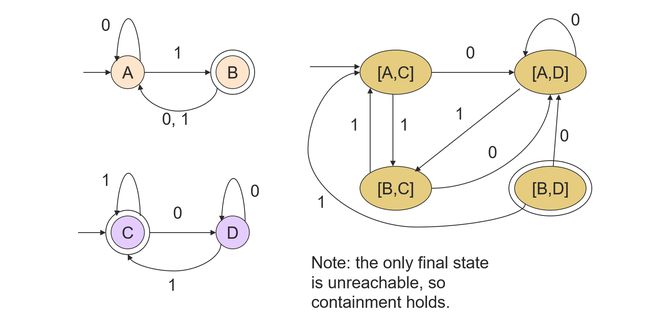
Decision Property: Containment

How do you define the final states [q.r] of the product so its language is empty iff L $\subseteq$ M

**Answer: ** q is final; r is not

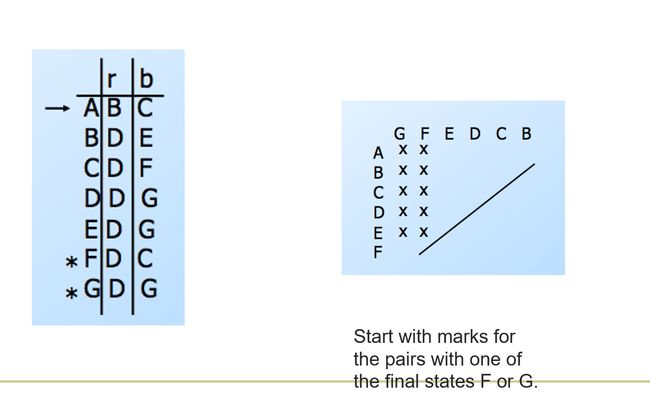
The Minimum-State DFA for a Regular Language

**Basis: ** Mark pairs with exactly one final state

**Induction: ** mark [q,r] if for some input symbol a, [$\delta (q,a),\delta (r,a)$] is marked

After no more marks are possible, the unmarked pairs are equivalent and can be into one state

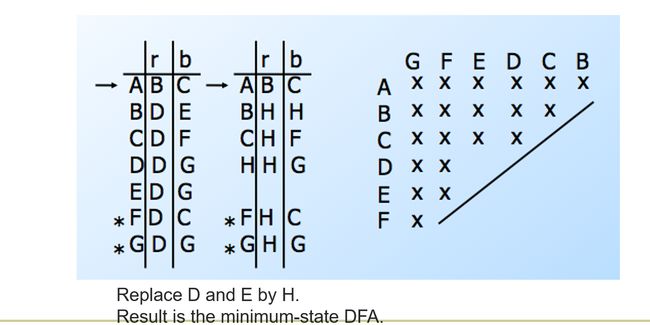
Constructing the Minimum-State DFA

• Suppose $q_1,...,q_k$ are indistinguishable states
• Replace them by one representative state q
• Then $\delta (q_1,a),...\delta (q_k,a)$ are all indistinguishable states.

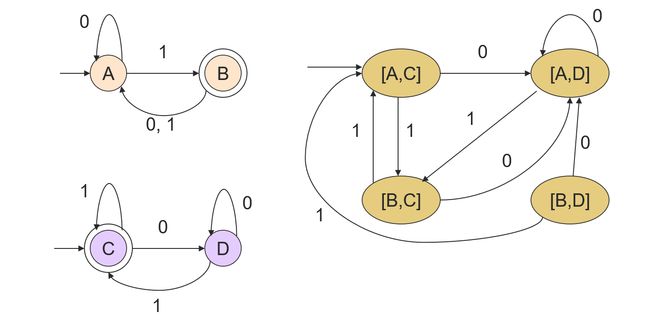
Example

Eliminating Unreachable States

The proof involves minimizing the DFA we derived with the hypothetical better DFA

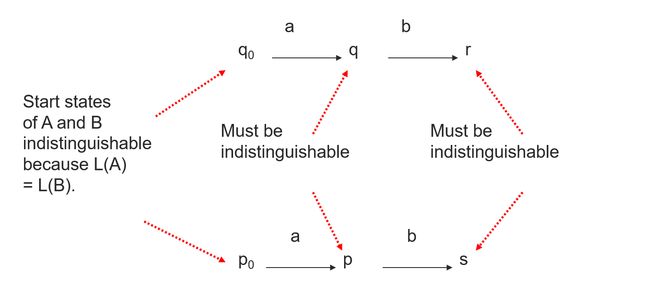
Proof: No unrelated, smaller DFA

IH: every state q of A is indistinguishable from some state of B

Proof

**Basis: ** Start states of A and B are indistinguishable

**Induction: ** Suppose w = xa, is a shortest string getting A to q

By IH, x gets to A to some state r that is indistinguishable from some state of B

Then ${\delta }_A(r,a)=q$ is indistinguishable from ${\delta }_B(p,a)$

However, two states of A cannot be indistingruishable from the same state of B, thus, B has at least as many states as A

Closure Properties of Regular Languages

Union

• If L and M are regular languages, so is L $\cup$ M

Intersection

• If L and M are regular languages, then so is L $\cap$ M
• Proof: Construct C, the product automaton of A and B

Difference

• If L and M are regular languages, then so is L - M
• Proof: Construct product automaton

Reversal

Proof: Let E be a regular expression for L, We show how to reverse E, to provide a regular expression E${}^R$ for L${}^R$

**Basis: ** If E is a symbol a, $ϵ$, or $\varnothing$, then E${}^R$ = E

**Induction: ** If E is

• F + G, then E^R = F^R + G^R
• FG, then E^R = G${}^R$ F${}^R$
• F${}^{\ast }$, then E^R = (F${}^R$)${}^{\ast }$

Homomorphisms

同态

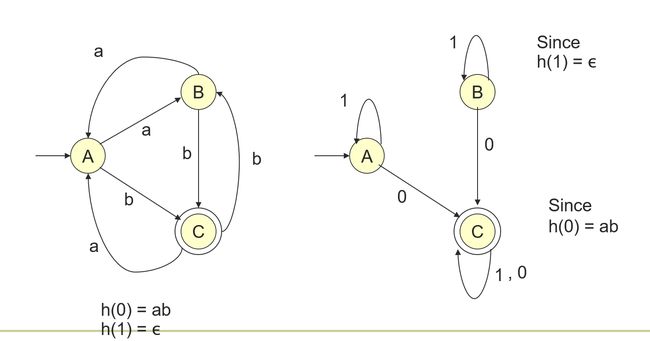
• A homomorphism on an alphabet is a function that gives a string for each symbol in that alphabet
• Example: h(0) = ab; h(1) = $ϵ$
• Extend to strings by h(a${}_1...$a${}_n$) = h(a${}_1$)…h(a${}_n$)
• Example: h(01010) = ababab

Closure Under Homomorphism

• If L is a regular language, and h is a homomorphism on its alphabet, then h(L) = {h(w)|w is in L} is also a regular language
• Proof: Let E be a regular language expression for L
• Apply h to each symbol in E
• Language of resulting RE is h(L)

Inverse Homomorphisms

• h$^{-1} = $ {w | h(w) is in L}

Example Inverse Homomorphisms

• Let h(0) = ab; h(1) = $ϵ$
• Let L = {abab,baba}
• h${}^{-1}$(L) = L($1^{\ast }01^{\ast }01^{\ast }$)

Closure Proof

• Start with a DFA A for L
• Construct a DFA B for h${}^{-1}$(L) with
  • the same set of states
  • the same start
  • the same final
  • Input alphabet = the symbols to which homomorphism h applies

${\delta }_B(q,a)={\delta }_A(q,h(a))$

• An induction on |w| (omitted) shows that $\delta (q_0,w)={\delta }_A(q_0,h(w))$
• Thus, B accepts w if and only if A accepts h(w)