深度学习，实验1：实现单隐藏层网络

数据集：planar dataset
实验内容：使用Pytorch实现含有单隐藏层的神经网络（节点数、损失函数、学习率等超参数原实验），完成数据分类

准确率要求：80%+  

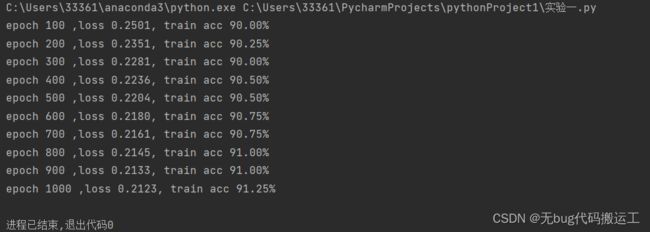
输出：不要求画图，要求显示每轮训练中的Loss及准确率

---

导入相应的数据集

import numpy as np
import torch
from torch import nn

#planar_utils.py提供的加载数据集方法
from planar_utils import load_planar_dataset
#加载数据集
def load_planar_dataset():
    np.random.seed(1)
    m = 400  # number of examples
    N = int(m / 2)  # number of points per class
    D = 2  # dimensionality
    X = np.zeros((m, D))  # data matrix where each row is a single example
    Y = np.zeros((m, 1), dtype='uint8')  # labels vector (0 for red, 1 for blue)
    a = 4  # maximum ray of the flower

    for j in range(2):
        ix = range(N * j, N * (j + 1))
        t = np.linspace(j * 3.12, (j + 1) * 3.12, N) + np.random.randn(N) * 0.2  # theta
        r = a * np.sin(4 * t) + np.random.randn(N) * 0.2  # radius
        X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
        Y[ix] = j

    X = X.T
    Y = Y.T

    return X, Y

---

定义网络模型，创建网络实例

class SingleNet(nn.Module):
    def __init__(self,input_size,hidden_size,output_size):
        super(SingleNet, self).__init__()
        self.hidden = nn.Linear(input_size,hidden_size)
        self.tanh = nn.Tanh()
        self.output = nn.Linear(hidden_size,output_size)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = self.hidden(x)
        x = self.tanh(x)
        x = self.output(x)
        x = self.sigmoid(x)
        return x
input_size,hidden_size,output_size = 2, 4, 1
net = SingleNet(input_size,hidden_size,output_size)

---

定义损失函数和优化器

cost = nn.BCELoss()
optimizer = torch.optim.SGD(net.parameters(), lr=1.2, momentum=0.9)

训练

#训练
def train(net,train_x,train_y,cost):
    num_epochs = 1000;
    for epoch in range(num_epochs):
        out = net(train_x)
        l = cost(out, train_y)
        optimizer.zero_grad()
        l.backward()
        optimizer.step()
        train_loss = l.item()

        if (epoch + 1) % 100 == 0:
            train_acc = evaluate_accuracy(train_x, train_y, net)
            print('epoch %d ,loss %.4f' % (epoch + 1, train_loss) + ', train acc {:.2f}%'
                  .format(train_acc * 100))

train(net, X, Y, cost)

输出结果：