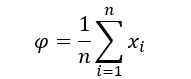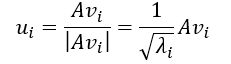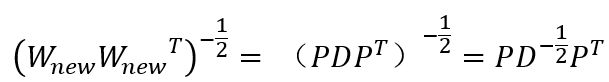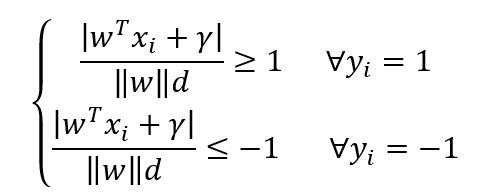SVM人脸识别（小白向，附代码）

上一篇最后说了要先更一篇AI的博文，先拿最近的实验作业补一补。主要讲解理论部分，文末自取链接。

LBP簇

LBP（Local Binary Pattern）

LBP(局部二值模式)是一种灰度测量的方法。其基本思想是在一个nxn的邻域内，用中心点的灰度值作为阈值，将其与周围8个点的灰度值进行比较得到一串8位的二进制编码，然后将编码的结果解码成十进制数赋给中心点的灰度值，恰好对应于灰度图的256种灰度值。
具体规则如下：如果周围点的像素值大于中心点的灰度值，那么将该位置置为1；如果周围点的灰度值小于中心点的灰度值，那么将该位置置为0。接着从中心点的左上位置开始顺时针遍历外围矩阵就得到了我们想要的二进制编码，接着解码成十进制数就得到了处理后的灰度值。
计算公式如下


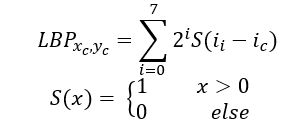
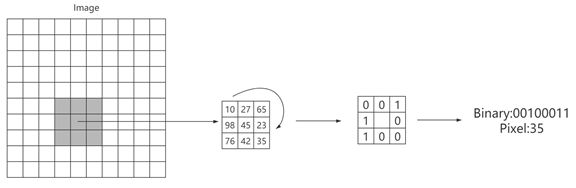
3x3邻域内的情况

n = 5 r = 2

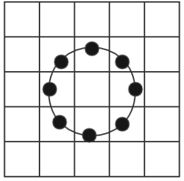
n = 5 r = 3
圆形LBP可以比较好地保留完整的图像信息，所以对特征向量的保留比较多，但这也导致特征提取后的图像大小没有发生改变。同时，由于圆形LBP的特征是通过邻域值的计算得到的，它可以确保局部特征不发生变化，而且由于计算时的方向性，圆形LBP得到的特征向量具有方向性，即同一张图旋转后得到的结果会发生改变。

使用圆形LBP进行特征提取后的人脸数据出现明显的马赛克。为了消除这种粗糙的像素点，我使用了双线性插值的方法让人脸数据变得更加平滑。

双线性插值法原理如下

由于圆形LBP算法是根据中心点画圆得到相邻8个点的坐标，所以实际得到的点坐标是一个小数，且一般不会出现在像素格的边界上。所以在LBP算子计算时可以加入双线性插值法来根据周围四个点计算得到更为正确的灰度值。
记Q点上下左右取整数值的点分别为Q_11、Q_12、Q_21、Q_22，Q点坐标值为(x，y)，Q_11的坐标值为(x_1,y_1)， Q_22的坐标值为(x_2,y_2)。
Q点在x,y两个方向上分别进行一次线性插值计算

其中f表示像素位置到图像灰度值的映射。
然后相加得到结果的灰度值。

经过双线性插值处理后的结果如下

可以发现双线性插值处理后的特征提取结果比处理前平滑很多。
经测试后发现圆形LBP的特征提取结果不是特别好，所以我又找到了LBP算法的其他分支来进行对比——旋转不变性LBP和统一模式LBP。

旋转不变性LBP

旋转不变性LBP是在圆形LBP的基础加以改进得到的。为了具有旋转不变性，
旋转不变性LBP重复了8次圆形LBP的计算过程，将所有的可能值都计算出来，然后选择其中的最小值作为中心点的灰度值。这使得同一张图即使经过旋转后还能得到相同的结果，改进了圆形LBP具有方向性的缺点。

等价模式LBP

一个LBP算子可以产生不同的二进制字符串，对于半径为r的圆形区域内含有p个采样点的LBP算子将会产生2^p种模式。为了解决二进制模式过多的问题,Ojala提出了采用一种“等价模式”来对LBP算子的模式种类进行降维。在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此，根据如下的规则可以进行数据降维：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式类。如00000000（0次跳变），00000111（只含一次从0到1的跳变），10001111（先由1跳到0，再由0跳到1，共两次跳变）都是等价模式类，除等价模式类以外的模式都归为另一类，称为混合模式类，例如10010111(共四次跳变)。

通过这样的改进，模式数量由原来的2^p种减少为p(p-1)+2种(p表示邻域集内的采样点数)。对于3x3邻域来说，8个点的二进制模式由256种减少为58种，它们对应的值按照从小到大分别编码为1-58，除了这些等价模式类之外的混合模式类被编码为0。因此，等价模式LBP特征图像整体偏暗（编码值对应灰度值）。这使得特征向量的存储空间和计算时的时间更少(单个灰度值仅需64位就可以存储)。并且由于高频噪声在这一过程中被计算为0或者很小的值，就能减少高频噪声带来的影响。

从处理结果上可以看出圆形LBP能比较完整地提取人脸面部的一些特征，旋转不变性LBP和等价模式LBP可以较好地提取人脸图片中的一些细节比如眼睛、嘴巴，甚至脸部肌肉的细节。旋转不变性LBP由于其在邻域内取8次旋转结果的最小值操作，所以整体的提取结果会比较暗（灰度值低）。但仅仅根据目前的提取结果来评判提取提取结果的优劣是不合理的，因为接下来的全局特征提取和分类器还会对特征进行变换和计算，而这些运算会决定哪些特征向量起分类的决定性因素。

PCA/ICA

数据降维对于SVM分类器而言是非常必要的。对SVM分类器而言，运算的时间复杂度取决于输入数据的维度n，不同的解法有不同的时间复杂度，常见的解法都在O(n)- O(n^3)之间。如果直接将局部特征提取的结果作为输入，那么SVM的训练时间会非常巨大。在本实验中，经过测试将400张112*92的图像输入到SVM分类器中进行训练，单次迭代的训练时间超过2小时。由于本实验需要进行不同的算法间的对比、K折交叉验证以及多次迭代，通过这种暴力训练的方式是非常不合理。因此，需要对图像进行降维。

PCA（主成分分析）

PCA是一种将多维数据降维的同时只丢失小部分特征向量的特征变换方法，PCA在很久之前就被应用到了人脸识别领域，也在数据降维过程中取得了不错的效果。在本次实验中，使用PCA对经过LBP算法得到的随机特征图像进行向量化操作，由于PCA本身的性质，能够在全局特征提取时对图像进行降维处理。

PCA推理如下
假设由LBP算法得到的人脸图像数据大小为[n,w,l]（n表示人脸图像数量，w表示图像宽度,l表示图像长度）。
1.先将该每张人脸图像变形为一维向量，即将[n,w,l]矩阵转换为[n,w*l]的矩阵。假设单张向量化的人脸图像用x_i表示，那么训练数据集x可以表示如下

2.计算平均脸φ

3.计算数据集内每张脸与平均脸的差值d

4.构建协方差矩阵A

需要求解出协方差矩阵C的特征值和特征向量，由于该矩阵的维度（wlwl）比较大,所以采用奇异值分解（SVD）来求得A^T A的特征值λ_i和特征向量V_i。
SVD推导过程如下：
假设矩阵A为MN的矩阵，将矩阵A映射到k维空间中（k=Rank（A））。现在的目标就是在n维空间中找到一组正交基V，使得A经过变换后还是正交的。
{v_1,v_2,…,v_n}
那么A矩阵的基映射就是
{Av_1,Av_2,…,Av_n}
如果两两正交，那么得到以下结果

根据假设的条件又有以下结论

所以如果正交基v选择为A^T A的特征向量，v之间两两正交

这样就找到了正交基使其映射后还是正交基，所以将映射的正交基单位化
因为

所以有

所以取单位向量

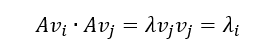
由此可得奇异值σ_i
σ_i=√(λ_i )
{u_1,u_2,…,u_k}正交基扩展成为{u_1,u,…,u_m } R^m空间的单位正交基，同样将
{v_1,v_2,…,v_k}扩展为 {v_1,v_2,…,v_n}(这n-k个向量要在Ax=0的解空间内)，所以对于在{v_1,v_2,…,v_n}中的v_j都有Av_j=0，因此σ_i=0。
由上述可得

得到A矩阵的奇异值分解结果（U是mm的正交阵，B是mn的对角阵，V是n*n的正交阵）
A=UBV^T
分析得：如果在n维空间中找到一个矩形，其边都落在A^T A的特征向量的方向上，那么经过A变换后的形状仍为矩形。
可以从上面的公式得出v_i为A^T A的右奇异特征向量，由u_i=Av_i得，u_i为A^T A的左奇异特征向量。

根据矩阵分块乘法展开得

结果需要表示成以下形式
A=XY
所以得到A的满秩分解结果为

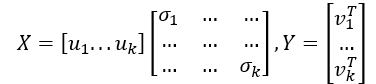
将数据输入即可获得对应的特征值。

5.根据特征值贡献率α选取前p个最大特征值及其对应的特征向量，贡献率指的是前i个特征值之和与所有特征值的和之比。

6.原协方差矩阵的特征向量w
w=(u_1,u_2,…,u_p)
差值投影到特征脸空间Ω
Ω_i=w^T d_i (i=1,2,…,200)
将这一结果Ω作为分类器的输入。

PCA提取结果（1024维，提取65维）
通过对图像的重建，可以得到PCA的结果。具体运算是将特征空间脸Ω右乘特征向量w的转置，再加上平均脸。这个过程相当于PCA逆操作，但由于特征向量本身减少了，所以还原的仅是提取结果后的PCA图像。
LBP+PCA提取结果如下图所示(以下均为PCA提取率为0.99的结果)

（均为112*92的图像，原特征个数为10304）

FastPCA（快速主成分分析）

假设A为图像矩阵， Z_nxm为A中每个样本减去平均值的矩阵。n为样本个数，m为样本维度。一般情况下，m远远大于n，协方差矩阵Z^T Z(mm)的大小也远远大于 ZZ^T(nn)，所以可以通过计算小矩阵的本征向量来计算大矩阵的本征向量。

假设向量v是ZZ^T的本征向量，那么
(ZZ^T )v=λv

两边乘Z^T得到
〖(Z〗^T Z〖)Z〗^T v=〖λZ〗^T v

所以将小矩阵的本征向量乘以Z^T就得到大矩阵的本征向量。
实际上，本次实验中的样本维度为112*92=1034，所以通过FastPCA能极大程度上地减少运算的时间。
以下是400张人脸图像处理总时间

FastICA（快速独立成分分析）

由于ICA（独立成分分析）是一个不定问题，没有确定解，所以本实验选择FastICA来对数据进行降维处理。作为两种比较广泛使用的降维算法，PCA寻找的是不相关因素，而FastICA寻找的是独立因素，即求解训练数据中的独立分量。本实验中使用这两种降维法，是为了寻找这两种算法在降维中的差异性，以及在人脸数据降维中的优劣性。

下图可以很好展示ICA和PCA的不同之处

左侧PCA，右侧ICA

FastICA算法的整体思路是基于特征向量（人脸图像中与决定其分类的特征向量）是可以通过高斯分布的线性组合来表示的，但特征向量本身是非高斯的。而FastICA就是基于该原理来对噪声进行高斯分离，得到其高斯表达。由于高斯分布的熵是最高的，因此通过计算概率分布函数的损失函数来对图像进行特征变换就可以得到对人脸识别起决定性作用的特征向量。

FastICA的理论基础Darmois-Skitovitch定理:

假设S_1,S_2,…,S_m是相互独立的源噪声，对于两个随机变量
X=a_1 S_1+a_2 S_2+⋯+a_n S_n
Y=b_1 S_1+b_2 S_2+⋯+b_n S_n
若X与Y独立，那么一定对于任意a_i b_i≠0,那么S_i一定是高斯分布。
所以，如果S_i不是高斯分布，而且X与Y不独立，那么a_i b_i=0。
FastICA算法分为三个部分：中心化、白化、迭代更新。
1.FastICA的中心化与PCA相同，都是将所有向量减去平均向量的差值作为下一步的输入X。

2.白化是求解互不相关的向量。
一定存在一个线性变换V，使得

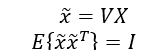
I表示初始输入的图像矩阵，E{x ̃x ̃^T }表示X的协方差矩阵C_x。
假设P是C_x的单位特征向量，D是C_x的特征值组成的对角阵，那么

这个V就是白化变换矩阵,由此可以解得

3.迭代更新的过程比较复杂，这里就不对其进行详细的原理推导，主要解释一下整体的思路。
首先初始化一组原矩阵的权重W_nxm（n是图像降维后维数，m是x ̃的行数）
然后每次迭代时先进行损失计算，公式如下

其中s=Wx ̃,g(x)是累积分布函数（cdf），本实验选择的是g（x）= tanh(x)

然后对W_new进行去相关处理

因为W_new 〖W_new〗^T是一个对角阵，所以

因此

然后计算W_new与W的一范数，如果值为0，那么该算法收敛，算法退出；否则继续迭代。

由于ICA算法输出的结果是s，该矩阵由x ̃和W相乘得到，在这一过程中可以实现图像的降维。找到了独立向量，由Darmois-Skitovitch定理可得，这些向量就可以近似看作服从高斯分布，所以这些向量具有较大的熵，也就是说它们对图像信息起决定作用，也就是PCA中特征贡献值高的向量。

原始图像ICA 圆形LBP+ICA 旋转不变LBP+ICA 等价模式LBP+ICA
在同样降维到80维的结果中可以看出，ICA和PCA效果相近，且都能比较完整地保留结果。

SVM

SVM（支持向量机）是一个非常经典的二分类器，它在人脸识别领域的应用较为成熟、效果较佳，且该二分类器可以通过集成的后处理来实现多分类，满足本实验的要求。

SVM具体思路如下

SVM是处理线性可分的数据的分类器，如果遇到线性不可分的数据，就将它们通过核函数映射到较高维度，只要维度数足够高，那么总能找到一个超平面将这两类数据分开。所以，SVM训练时的数据总是线性可分的。

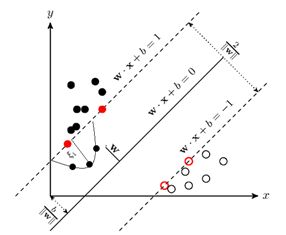
对于线性可分的两类数据，有很多个超平面可以将其分开，SVM分类器就是求解一个最优的超平面。如下图所示，红蓝二维数据间存在很多的条直线可以将其分开。

但这两个分类直线存在着性能上的差异。如下图所示，如果我再加入一个新的红点，那么在b分类器中分类正确，而在c分类器中分类错误。这是由于b分类器的分类间隔比c分类器的分类间隔大，即b分类器分界线上点到中心线的距离大。

为了得到最优的分类器，SVM所寻找的分类超平面只有一个，那就是分类间隔最大的分类超平面，而该超平面在理论上具有最优的性能。但实际来说，该平面具有最优性的前提是训练数据能高度概括测试数据，并且它们具有相似的分布。否则，该平面的最优性就不能成立。所以，在训练数据足够大的情况下，SVM的分类平面就能分类绝大多数的数据。

可以通过二维数据的分割结果发现，SVM所求解的是当2/‖w‖ 取最大值时，对应的超平面方程。

下面是理论推导

输入数据为X，超平面权重为W，超平面偏置为γ，那么分类间隔即为

为了给两类数据赋上标签-1和1，则可得如下方程组

两边除以d得到

由于w是一个二阶矩阵，所以‖w‖、d都是标量。所以上式描述的是一条直线的法向量和截距，由此得到需要求解的超平面方程就是w^T x_i+γ=0，根据定义的分类标准可以得到如下方程，这也是-1和1作为分类标签的好处，可以方便计算。

由于求解的目标是max⁡(2/‖w‖ )，这就等价于求解min ‖w‖/2的情况，为了方便后面的求导这里将求解目标变为min(〖‖w‖/2〗^2)。

由于该问题是约束最优化问题，而且目标函数为二次，约束条件是线性的，这是个凸二次规划。二次规划问题同样可以转化为对偶问题，并且对偶问题更容易求解，所以使用拉格朗日对偶法来对求解目标进一步变形

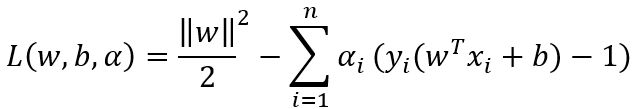
其中α是拉格朗日乘子，α≥0。
由于线性规划问题存在最优解的充要条件是满足KKT条件。
所以问题转化为L(w,b,α)对w、b求最小，再对α求最大。
为了使得L(w,b,α)最小，分别对w和b求导数，并使其都等于0

将结果代回到原函数L，并将其展开后化简得到

所以原问题变为

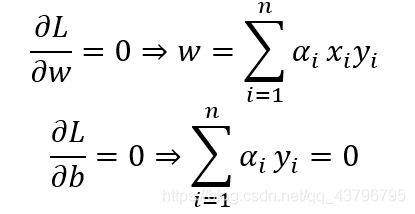
以上是线性可分SVM的求解过程，但实际数据不一定线性可分，所以需要加一个松弛变量ξ_i≥0来使得约束条件y_i （w^T x_i+γ）≥1-ξ_i可以是适应于分类间隔内的点。所以目标函数由〖‖w‖/2〗^2变为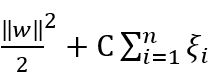
(C为惩罚系数)
这样就可以实现“软间隔”的支持向量机。

“软间隔”SVM的目标函数最后与“硬间隔”SVM相同，但α_i的条件变为0≤α_i≤C。

接下来使用SMO算法进行SVM具体值求解,SMO算法的思路是选择两个变量，固定其他变量，来构建一个新的二次规划的问题。
为了将数据转为线性数据，往往引入K核函数对x进行变换,设K_ij=K(x_i,x_j),线性核函数中K_ij=〖x_i*x〗_j
假设选择的两个变量分别为α_1，α_2，其他变量α_i(i=1,2,…,N)不变。那么如下公式

就可以转换为

根据∑_(i=1)^n▒α_i y_i=0可得

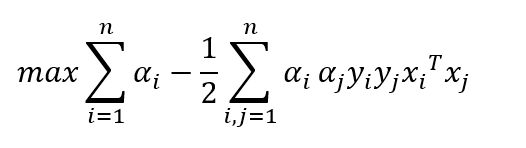
由于y_i是1或-1，所以y_i y_i=1，上式两边乘以y_i可以得到

将α_1带入到W(α_1,α_2)可以得到W（α_2）
令

其中F是将无关变量合并的常数项

求其极值点即导数为0的情况

因为SVM对数据点的预测值为f(x)= ∑_(i=1)^n▒α_i y_i K(x_(i ),x)+b,因此

记E_i=f(x_i)- y_i, 〖η=K〗_11+K_22-2K_12，将v_1 和v_2代入到∂W/(∂α_2 )表达式，即可得到


通过上图可知当y_1≠y_2时，〖α_2〗^new的取值范围是min(C,C-k),max(0,-k); 当y_1=y_2时，〖α_2〗^new的取值范围是min(C,k),max(0,k-C)
阈值b也会影响到f（x）的计算，所以b也需要不断更新。由于b的计算过程与α类似，所以这里直接给出公式。
当〖α_1〗^{new和〖α_2〗}new在(0,C)范围内时，

此时b=〖b_1〗^{new=〖b_2〗}new
如果〖α_1〗^new 与〖α_1〗^new 均为0或者C,则b=0.5(〖b_1〗^{new+〖b_2〗}new)

至此，SVM已通过SMO方法求得超平面。

但是为了得到多分类结果，需要训练多个分类器来区分不同的类，具体思路分为以下两种：

1.一对一（one-against-one）,如果有k类，就在每两类之间构造出一个分类器，一共构造了1/2 K（K-1）个分类器。测试时，分类器会采取投票法，得票数最多的点就是新点归属的类。

2.一对多（one-against-all），如果有k类，就构造出k个二分类器。第i次训练时，将样本中第i类作为正训练样本，其余作为负训练样本。测试时，将所有分类器分类结果的最大值作为最终分类结果。

一对一训练速度较一对多快，这是因为一对一单次训练时数据量较小。但是，其训练的分类器数量较多。而且若单个二分类器存在不规则化，那么整个K分类器就会趋向于过学习。而一对多分类器没有上述的风险，但是训练时间较长。

期末有点忙，所以下篇还是作业，AI的博文等到有空再更新了。

代码链接：https://pan.baidu.com/s/1TlGQ51gIYdV3_IOZGIuOjw 提取码：7392