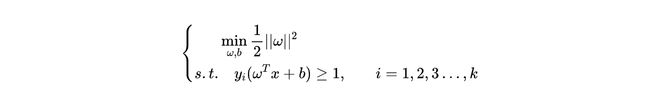机器学习 | 深入SVM原理及模型推导(一)
本文始发于个人公众号:TechFlow,原创不易,求个关注
今天是机器学习专题的第32篇文章,我们来聊聊SVM。
SVM模型大家可能非常熟悉,可能都知道它是面试的常客,经常被问到。它最早诞生于上世纪六十年代。那时候虽然没有机器学习的概念,也没有这么强的计算能力,但是相关的模型和理论已经提出了不少,SVM就是其中之一。
SVM完全可以说是通过数学推导出来的模型,由于当时还没有计算机,所以模型当中的参数都是数学家们用手来算的。它有一个巨大的应用就是前苏联的计划经济体系,我们知道在计划经济当中,国家有多少社会资源,每样商品需要生产多少都是国家统筹规划的。
但是国家和社会不是一成不变的,去年消耗了多少粮食不意味着今年也会消耗这么多,很多因素会影响。所以当时前苏联的科学家们用当时最先进的方法来计算参数预测各项商品的消耗来完成社会资源的调度,这个最先进的方法就是SVM。
废话说了这么多,下面我们就来看看这个模型实际的原理吧。
算法描述
SVM的英文全称是Support Vector Machine,翻译过来的意思是支持向量机。无论是英文还是中文,我们直观上有些难以理解。
难以理解没有关系,我们先把支持向量这个概念放一放,先来介绍一下它整体的原理。
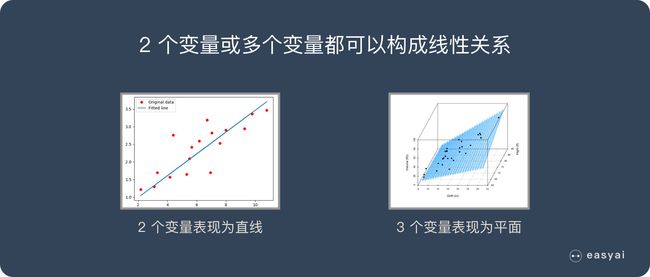
SVM最基本的原理就是寻找一个分隔“平面”将样本空间一分为二,完成二分类。进一步我们可以知道,对于二维的平面,我们要分隔数据需要一条线。对于三维的空间我们要分开需要一个面,发散开去对于一个n维的空间,我们要将它分开需要一个n-1的超平面。
SVM寻找的就是这样的超平面,为了方便理解,我们以最简单的二维场景为例。
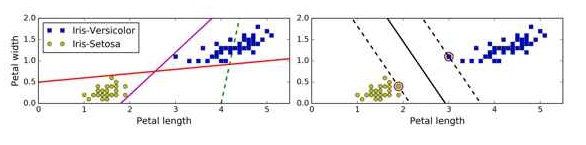
我们观察一下上图,很明显图中的数据可以分成两个部分。对于上图的数据而言理论上来说我们有无数种划分的方法,我们既可以像左边这样随意的划分,也可以像右边这样看起来严谨许多的划分,在这么多划分方法当中究竟哪一种是最好的呢?我们怎么来定义划分方法的好和坏呢?
SVM对这个问题的回答很干脆,右图的划分是最好的,原因是它的间隔最大。
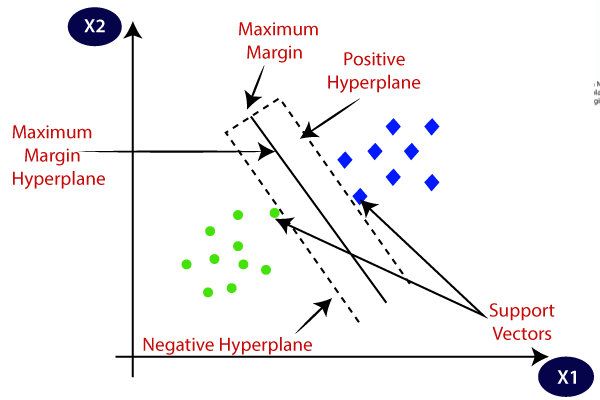
从图中我们可以看到,间隔也就是被划分成两个部分之间最接近的距离,间隔正中的这条红线就是SVM找到的用来划分的超平面。
我们进一步观察可以发现,对于间隔这个事情来说,绝大多数样本都不起作用,能够起作用的只有在落在虚线上也就是间隔边缘的样本。是这些样本确定了间隔,从而间接确定了分隔平面,支撑起了模型。
所以SVM当中把这些落在边缘上的样本成为支持向量,这也是SVM得名的由来。
模型推导
我们首先来考虑最简单的情况,即线性可分,也就是说所有样本都可以被正确的划分。这样划分出来得到的间隔是实实在在的,所以我们把线性可分的情况下的间隔称为硬间隔。
首先我们先写出这个分隔平面的公式:
ω T x + b = 0 \omega^Tx+b = 0 ωTx+b=0
其中x表示一条n维的样本特征组成的向量, ω \omega ω是平面的n维法向量,决定平面的方向。虽然从公式上来看和线性回归很像,但是它们之间的本质区别是线性回归是用来拟合label的,而SVM的平面方程是用来确定平面方向的。这里的b就是简单的偏移量,表示平面距离原点的距离。
表示出来分隔平面之后,我们就可以表示出每一个样本距离平面的距离:
γ = ∣ ω T x + b ∣ ∣ ∣ ω ∣ ∣ \gamma = \frac{|\omega^Tx + b|}{||\omega||} γ=∣∣ω∣∣∣ωTx+b∣
这个公式看起来好像不太明白,其实它是由二维的点到平面的距离公式演化得到的: d = ∣ A x + B y + c ∣ A 2 + B 2 d = \frac{|Ax + By + c|}{A^2 + B^2} d=A2+B2∣Ax+By+c∣
这里的 ∣ ∣ ω ∣ ∣ ||\omega|| ∣∣ω∣∣是一个L2范数,我们把它也展开可以写成: ∣ ∣ ω ∣ ∣ = ∑ i = 1 k ω i 2 ||\omega|| = \sqrt{\sum_{i=1}^k \omega_i^2} ∣∣ω∣∣=∑i=1kωi2
模型假设
这里我们做一点假设,对于样本当中的点,在分隔平面上方的类别为1,在分隔平面下方的类别为-1。那么我们可以进一步得到** ω x i + b \omega x_i +b ωxi+b应该和 y i y_i yi同号**。所以我们可以写成: y ( ω T x + b ) > 0 y(\omega^T x + b) > 0 y(ωTx+b)>0。
我们来观察支持向量,也就是刚好在间隔边缘的点,它们到分割平面的距离刚好是间隔的一半。我们假设这个点的函数值是 γ \gamma γ,我们把它表示出来可以得到:
y i ( ω T x i + b ) = γ y i ( ω γ x i + b γ ) = 1 \begin{aligned} y_i(\omega^T x_i + b)&=\gamma\\ y_i(\frac{\omega}{\gamma}x_i + \frac{b}{\gamma}) &= 1 \end{aligned} yi(ωTxi+b)yi(γωxi+γb)=γ=1
我们令新的 ω ^ = ω γ \hat{\omega} = \frac{\omega}{\gamma} ω^=γω,新的 b ^ = b γ \hat{b}= \frac{b}{\gamma} b^=γb。也就是说我们通过变形可以将函数值缩放到1,为了方便计算,我们选取恰当的参数,使得间隔刚好为1。既然如此,对于所有的样本点,我们都可以得到 y i ( ω T x i + b ) ≥ 1 y_i(\omega^Tx_i + b) \ge 1 yi(ωTxi+b)≥1,对于支持向量来说 y i ( ω T x i + b ) y_i(\omega^Tx_i + b) yi(ωTxi+b)=1。
利用这点,我们可以表示出间隔:
γ = 2 ∣ ω T x + b ∣ ∣ ∣ ω ∣ ∣ = 2 ∣ ∣ ω ∣ ∣ \gamma = 2\frac{|\omega^Tx + b|}{||\omega||} = \frac{2}{||\omega||} γ=2∣∣ω∣∣∣ωTx+b∣=∣∣ω∣∣2
2 ∣ ∣ ω ∣ ∣ \frac{2}{||\omega||} ∣∣ω∣∣2是一个分数,我们要求它的最大值,也就是求 ∣ ∣ ω ∣ ∣ 2 ||\omega||^2 ∣∣ω∣∣2的最小值。我们想要在线性可分的基础上让这个间隔尽量大,所以这是一个带约束的线性规划问题,我们把整个式子写出来:
接下来我们要做的就是在满足约束的前提下找到使得 1 2 ∣ ∣ ω ∣ ∣ 2 \frac{1}{2}||\omega||^2 21∣∣ω∣∣2最小的 ω \omega ω,这个式子看起来非常麻烦,又有不等式掺和在里面,那么我们应该怎么办呢?
这部分内容我们将会在下一篇文章分享,敬请期待。
今天的文章到这里就结束了,如果喜欢本文的话,请来一波素质三连,给我一点支持吧(关注、转发、点赞)。