【论文精读】NeRF详解
最近阅读了开启三维重建新纪元的经典文章《NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis》,接下来会更新NeRF系列的论文精读、代码详解,力求做到全网最细!欢迎大家关注和交流!
论文链接:论文
代码链接:Github (这是官方代码,是tensorflow版本)
Abstract
文章提出了一种合成复杂场景的新视角图片的方法,使用一组稀疏的输入视图来优化底层的连续体积场景函数。算法只需要使用全连接网络(而不需要卷积),仅需的输入是单个连续 5D 坐标,也就是空间位置 ( x , y , z ) (x, y, z) (x,y,z) 和观察方向 ( θ , φ ) (θ, φ) (θ,φ),而输出是在那个空间位置的volume density(体积密度)和依赖于视图的radiance。我们通过沿相机光线查询 5D 坐标来合成视图,并使用经典的体积渲染技术将输出的颜色和密度投影到图像中。因为volume rendering是可微分的,所以输入方面只需要已知pose的图片了。文章描述了如何有效地优化神经辐射场以渲染新视图,并展示了优于先前神经渲染和视图合成工作的结果。
1. Introduction
将静态场景表示为一个连续的 5D 函数,该函数输出空间中每个点$ (x, y, z)$ 在每个方向 ( θ , φ ) (θ, φ) (θ,φ) 发射的辐射,以及每个点的density,其作用类似于不透明度,控制穿过 ( x , y , z ) (x, y, z) (x,y,z) 的光线会累积很多少辐射。文章通过MLP来表示这个映射。
为了渲染从特定角度的神经辐射场,我们:1) 将相机光线穿过场景以生成一组采样的 3D 点,2) 使用这些点及其对应的 2D 观察方向作为神经网络的输入,以生成一组颜色和密度的输出,以及 3) 使用经典的体积渲染技术将这些颜色和密度累积到 2D 图像中。整个pipeline如下图:
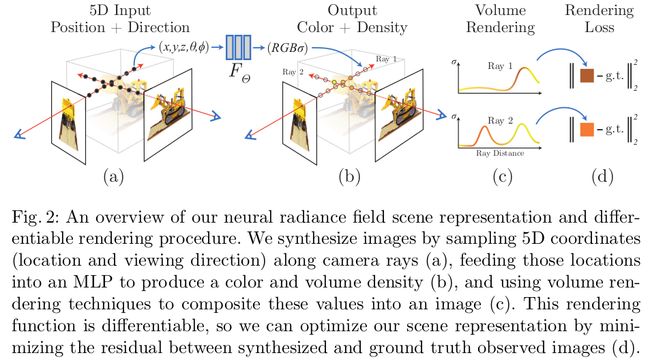
我们发现,针对复杂场景优化神经辐射场表示的基本实现不能收敛到足够高分辨率的表示,并且在每条摄像机光线所需的样本数量方面效率低下。所以文章将5D输入通过位置编码得到新的形式,使得MLP表征更高的频率,我们还使用层级式的采样,以减少采样此高频场景所需的查询数量。
文章提出的方法继承了体积表示的优点:两者都可以表示复杂的现实世界几何和外观,并且非常适合使用投影图像进行基于梯度的优化。 至关重要的是,该方法在对复杂场景进行高分辨率建模时克服了离散体积网格的高昂存储成本。总的来说文章主要贡献有:
- 把一种复杂的场景表示为 5D 神经辐射场的方法,并参数化为 MLP 网络。
- 基于可微渲染过程,我们优化这种场景表示。 这包括分层采样策略,用于将 MLP 的容量分配给具有可见场景内容的空间。
- 一种位置编码方式被使用,使我们可以成功优化神经辐射场以表示高频场景内容。
2. Related Work
2.1 Neural 3D shape representations
近年的工作通过优化将 x y z xyz xyz 坐标映射到signed distance functions或occupancy fields的深度网络,研究了连续 3D 形状的隐式表示。然而,这些模型需要有 3D 几何形状的ground truth作为真值。后来的一些工作制定了只需要使用 2D 图像就可以优化神经隐式形状表示的可微渲染函数。Niemeyer等人将物体表面表示为 3D occupancy fields,并使用数值方法找到每条射线的表面交点,然后使用隐式微分计算精确导数。每个光线交点位置都作为神经 3D texture field的输入,这个field预测该点的漫反射颜色。Sitzmann等人使用一种更加不直接的神经 3D 表示,在每个连续的 3D 坐标处简单地输出一个特征向量和 RGB 颜色,并提出一个由循环神经网络组成的可微渲染函数,该网络沿着每条射线行进以确定表面的位置。虽然这些方法有表示复杂和高分辨率形状的潜力,但是目前仍然只能表达简单的几何形状。
2.2 View synthesis and image-based rendering
给定密集的采样视角,新视角可以通过light field sample interpolation技术得到。如果是对于更稀疏的采样,就需要从观察到的图像中预测传统的几何和外观表示。一种流行的方法使用基于网格的场景表示,具有漫反射或与视图相关的外观。Differentiable rasterizers或pathtracers可以使用梯度下降直接优化网格表示以重现一组输入图像。然而,基于图像重投影的基于梯度的mesh优化通常很困难,可能是因为局部最小值或缺失的景观部分条件太差了。 此外,该策略需要在优化之前提供具有固定拓扑的模板网格作为初始化,这通常不适用于无约束的现实世界场景。
另一类方法使用体积。体积方法能表示复杂的形状和材料,非常适合基于梯度的优化,并且比基于mesh的方法产生的视觉干扰更少。早期的体积方法使用观测到的图像来直接给体积上色。近期,一些方法使用多个场景的大型数据集来训练深度网络,从一组输入图像中预测采样的体积表示,然后使用 alpha-compositing或沿光线学习的合成来在测试时渲染新的视图。其他工作针对每个特定场景优化了CNN和采样体积网格的组合,使得 CNN 可以补偿来自低分辨率体积网格的离散化伪影,或者允许预测的体积网格根据输入时间而变化。虽然这些体积技术在新视图合成方面取得不错的结果,但它们扩展到更高分辨率图像的能力受到了限制,因为离散采样导致时间和空间复杂度高,而渲染更高分辨率的图像需要对 3D 空间进行更精细的采样。文章提出的方法通过在MLP的参数中编码连续volume来规避这个问题,这不仅产生比先前体积方法更高质量的渲染,而且只需要更小的存储成本。
3. Neural Radiance Field Scene Representation
我们将一个连续的场景表示成一个3D坐标点x = (x, y, z)和2D视角方向(θ, φ)作为输入、颜色c = (r, g, b)和体积密度σ作为输出的函数。实践中,我们把方向表示为3D 笛卡尔单位向量 d。我们用 MLP 逼近这种连续的 5D 场景表示 F Θ : ( x , d ) → ( c , σ ) F_{Θ} : (x, d) → (c, σ) FΘ:(x,d)→(c,σ)并优化权重 Θ Θ Θ。我们通过让网络把体积密度 σ σ σ 预测为仅与位置 x x x有关,来保证这种表征方法在不同视图下是一致的,同时将 RGB 颜色 c c c 预测为位置和观察方向的函数。为了达到这个,MLP首先把3D坐标 x x x通过8层全连接层(激活函数为ReLU,每层256通道),输出体积密度 σ σ σ和一个256维的特征向量。然后将该特征向量与相机光线的观察方向concatenate起来,并传递到一个额外的全连接层(激活函数为ReLU,128 个通道),该层输出与视图相关的 RGB 颜色。
4. Volume Rendering with Radiance Fields
5D 神经辐射场将场景表示为空间中任意点的体积密度和定向发射的辐射。我们使用经典体积渲染的原理,来渲染任何穿过场景的光线的颜色。体积密度 σ ( x ) σ(x) σ(x)可以解释为射线终止在位置 x x x 处无穷小粒子的微分概率。而期望的颜色 C ( r ) C(r) C(r)(相机光线 r ( t ) = o + t d r(t) = o + td r(t)=o+td,近处远处界限为 t n t_{n} tn和 t f t_{f} tf)可以被表示为: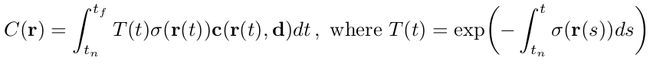
函数T(t)表示沿着光线从tn到t的accumulated transmittance,也就是光线从tn穿到t却不打到任何粒子的概率。从我们的连续神经辐射场渲染新视图,需要估算积分 C ( r ) C(r) C(r),虚拟相机上的每个像素都需要一条光线。
我们使用quadrature来求这个连续积分。通常用于渲染离散体积网格的deterministic quadrature将限制我们表示的分辨率,因为 MLP 只会在固定的离散位置集上被查询。取而代之的是,我们使用分层抽样方法,将 t n t_{n} tn到 t f t_{f} tf拆分为N个均匀分布的区间, i i i从 1 1 1到 N N N,然后从每个区间中随机均匀抽取一个样本:
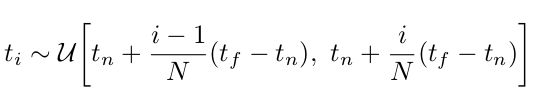
尽管我们使用一组离散的样本来估算积分,但分层采样使我们能够表示连续的场景表示,因为它导致在优化过程中在连续位置对 MLP 进行评估。我们使用这些样本通过quadrature rule估计 C ( r ) C(r) C(r),也就是文中的等式3:
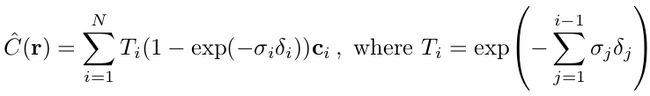
其中 δ i = t i + 1 − t i δ_{i} = t_{i+1} − t_{i} δi=ti+1−ti 是相邻样本之间的距离。这个从 ( c i , σ i ) (c_{i} , σ_{i}) (ci,σi) 值的集合中计算 C ^ ( r ) Ĉ(r) C^(r) 的函数是微分的,并简化为alpha 值 α i = 1 − e x p ( − σ i δ i ) α_{i} = 1 − exp(−σ_{i} δ_{i} ) αi=1−exp(−σiδi) 的传统alpha合成。
什么是alpha合成?
Alpha合成(alpha compositing)是一种将图像与背景结合的过程,结合后可以产生部分透明或全透明的视觉效果。图像里记录着每个像素的颜色信息,额外的信息以 0 和 1 之间的值表示,记录在Alpha通道里。0 表示该像素是透明的,即图中的几何体没有覆盖到本像素;而 1 则表示像素不透明,几何体完全覆盖了此像素。
Alpha混合(alpha blending)是将半透明的前景色与背景色结合的过程,可以得到混合后的新颜色。前景色的透明度不限,从完全透明到完全不透明都可以。如果前景色完全透明,混合后的颜色就是背景色;如果前景色完全不透明,混合后的颜色就是前景色;如果在这两种极端情况之间,混合后的颜色可以通过前景色和背景色的加权平均计算。
5. Optimizing a Neural Radiance Field
文章在上一节描述了将场景建模为神经辐射场并从该表示中渲染新视图所必需的核心组件。 然而,这些组件不足以实现最好的质量。 我们引入了两项改进以支持表示高分辨率复杂场景。 第一个是输入坐标的位置编码,有助于 MLP 表示高频函数,第二个是分层采样过程,它允许我们有效地采样这个高频表示。
5.1 Positional encoding
虽然神经网络是一个通用的函数逼近器,我们发现直接对5D输入进行操作会导致渲染在表示颜色和几何形状的高频变化方面表现不佳。在将输入传递到网络之前,使用高频函数将输入映射到更高维空间可以更好地拟合包含高频变化的数据。
将 F Θ F_{Θ} FΘ 重新定义为两个函数的组合 F Θ = F Θ ′ ◦ γ F_{Θ} = F_{Θ} '◦ γ FΘ=FΘ′◦γ,一个是学习的,一个不是,明显提高了性能。 γ γ γ是一个实数域向更高维度空间的映射 R 2 L \mathbb{R^{2L}} R2L ,另一个仍然是前文提到的那个简单MLP。
![]()
这个函数对 x x x坐标的3个值和向量 d d d的三个值都进行了编码。实验中设置了 L = 10 L = 10 L=10 for γ ( x ) γ(x) γ(x) and L = 4 L = 4 L=4 for γ ( d ) γ(d) γ(d)。
5.2 Hierarchical volume sampling
我们在沿每条摄像机光线的 N N N 个查询点处密集评估神经辐射场网络的渲染策略效率低下:没有贡献的空间和遮挡区域仍然被重复采样。 我们从体积渲染的早期工作中汲取灵感,通过分层样本来提高渲染效率,使其与最终渲染的预期效果成正比。
我们不只是使用单个网络来表示场景,而是同时优化两个网络:一个“粗糙”和一个“精细”。 我们首先使用分层抽样对一组 N c N_{c} Nc 个位置进行抽样,并评估这些位置的“粗略”网络。给定这个“粗略”网络的输出,我们然后沿着每条射线采样,其中样本偏向与体积相关的部分。 为此,我们首先在方程式中重写粗网络 C ^ c ( r ) Ĉ_{c} (r) C^c(r) 中的 alpha 合成颜色作为沿射线的所有采样颜色 c i c_{i} ci 的加权和:
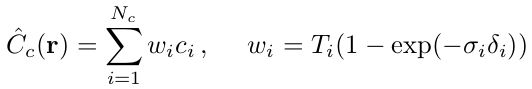
将这些权重归一化为 w ^ i = w i / ∑ j = 1 N c w j ŵ_{i} = w_{i}/\sum^{N_{c}}_{j=1}{w_{j}} w^i=wi/∑j=1Ncwj沿射线生成分段常数概率密度函数。我们使用逆变换采样从该分布中采样第二组 N f N_{f} Nf个位置,在第一组和第二组样本的并集评估我们的“精细”网络,并使用等式3计算射线的最终渲染颜色 C ^ f ( r ) Ĉ f (r) C^f(r) ,但使用所有 N c + N f N_{c} +N_{f} Nc+Nf 个样本。此过程将更多样本分配给我们期望包含可见内容的区域。 这达到了与importance sampling类似的目标,但我们将采样值用作整个积分域的非均匀离散化,而不是将每个样本视为整个积分的独立概率估计。
5.3 Implementation details
输入:场景的一系列RGB图片,对应的相机位姿和内参,和场景的bounds。
在每次优化迭代中,我们从数据集中所有像素的集合中随机采样一批相机光线,然后按照第 2 节中描述的分层采样,从粗网络中查询 N c N_{c} Nc 个样本,从细网络中查询 $N_{c} + N_{f} 个样本。 然后我们使用渲染过程,渲染来自两组样本的每条光线的颜色。我们的loss只是粗略和精细渲染的渲染像素颜色和真实像素颜色之间的总平方误差:
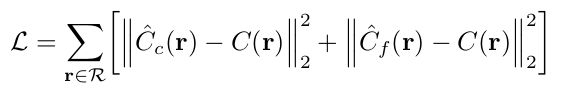
参数设置:batch size=4096 rays,每个在粗略中的 N c = 64 N_{c} = 64 Nc=64 个坐标和精细中的 N f = 128 N_{f} = 128 Nf=128 个附加坐标处采样。其余参数详情可见文章。
6. Results & Conclusion
在数据集上进行了实验,效果很好。
总结也不用解读了,当然是新颖又高效。
