NeRF神经辐射场学习笔记（七）— NeRF-W论文翻译及原理解读

声明

本人书写本系列博客目的是为了记录我学习三维重建领域相关知识的过程和心得，不涉及任何商业意图，欢迎互相交流，批评指正。

论文概述

NeRF-W（NeRF in the wild）针对于传统NeRF有关光照变换（variable illumination）和瞬时遮挡（transient occluders）的局限，提出了改进方案。文章引入了一些新的观点使得能够利用非结构化图像集合（instructured image collections）进行场景重建；

• 首先，在一个学习过的低维潜在空间（learned low-dimensional latent space）中建模每个图像的外观变化，如曝光、光照、天气和后期处理。 遵循生成性潜在优化（Generative Latent Optimization）的框架，我们对每个输入图像的外观嵌入（appearance embedding）进行优化，从而通过学习整个图片集合中的共享外观表示（shared appearance representation），使NeRF-W具有灵活性来解释图像之间的光度和环境变化（photometric
  and environmental variations）。
• 其次，文章利用了一个融合有数据相关不确定场的次级体素辐射场（a secondary volumetric radiance field combined with a data-dependent uncertainty field），其中不确定场的提出捕获了可变的观测噪声，并进一步降低了瞬态对象对静态场景表示的影响。通过优化能够识别和消除瞬时图像内容，我们可以通过只渲染静态部分来合成新视图的真实感渲染。
  

问题的提出

NeRF-W目的是通过一组非结构化的数据集（比如来自互联网上的照片集）来渲染场景，而这样的目的也违反了传统的NeRF网络中采用同样条件下采集的输入图片进行优化的这种前提——换句话说，就是违反了在两个不同的图像中从相同的位置和观看方向观察到的三维空间中的一个点具有相同的深度的这种假设。原因有两点，一是光度变化（Photometric variation，户外摄影的照片亮度产生不一致）、二是瞬态物体（Transient objects，遮挡物以及动态的物体对重建场景的影响）

NeRF-W主要观点

1.潜在外观建模（Latent Appearance Modeling）

为了使NeRF适应光度变化的问题，文章采用了Generative Latent Optimization（GLO）的方法——令每张图像${\mathcal{T}}_i$都附带一个长度为$n^{(a)}$的实外观嵌入向量${ll}_i^{(a)}$。（real-valued appearance embedding vector）并且重新定义了与图像相关的辐射值${cc}_i(t)$，以及最后合成后的像素颜色${\widehat{CC}}_i$：$$\begin{gathered} {\widehat{CC}}_i(rr)=\mathcal{R}(rr,{cc}_i,\sigma ), \\ {cc}_i(t)={\text{MLP}}_{{\theta }_2}(zz(t),{\gamma }_{dd}(dd),{ll}_i^{(a)}) \end{gathered}$$使用这些${ll}_i^{(a)}$作为仅向网络中传递颜色信息分支的输入数据，使模型可以自由地改变特定图像中场景的辐射亮度，同时仍然保证场景信息（不透明度$\sigma (t)$以及网络加工后的位置信息$zz(t)$）是静态的，并在所有图像中共享。

2.瞬态物体现象（Transient Objects）

文章使用两个观点来解决瞬态物体的遮挡现象：

第一个观点：

将传统的NeRF MLP网络结构视为静态网络（static）其中包括上文提到的光度输入、随之定义了一个瞬态网络（transient），结构与NeRF相似，输入位置信息与方向信息后得到另一组颜色与不透明度结果；这使得NERF-W既能够学习和渲染重建包含瞬态物体的图像，也能够保证与静态网络的分离，不会对静态场景的表示引入伪影。
对于瞬态网络而言，也需要构建其体素渲染的流程（计算公式与NeRF的一样，这里就不写了，太难敲了），并且利用得到的瞬态${\sigma }_i^{(\mathcal{T})}(t)$和${cc}_i^{\mathcal{T}}(t)$结果来扩充静态输出的${\sigma }_i(t)$和${cc}_i(t)$，以及用来合成最终的预测像素颜色$rr(t)$；

第二个观点：

在瞬态网络中引入另一个参数——不确定度（uncertainty，用来忽略不可靠的像素和可能包含遮挡物的三维位置）
按照文章的说法，利用 Kendall 的贝叶斯学习框架，来建模观测颜色的不确定性，即用一个依赖图像和光线的各向同性的正态分布（方差是${\beta }_i(rr{)}^2$，均值是${\widehat{CC}}_i(rr)$）来建模颜色信息${CC}_i(rr)$。换句话说，就是将渲染颜色的这个过程用上述框架进行建模，找到合适的对应参数，那么不确定度，即方差在该模型下的表述就可以近似类比为渲染的颜色结果：${\hat{\beta }}_i(rr)=\mathcal{R}(rr,{\beta }_i,{\sigma }_i^{(\mathcal{T})})$（这只是我的个人理解，不一定对）。紧接着将该不确定度变量也放入瞬时网络中作为输入：$$\left[{\sigma }_i^{(\mathcal{T})}(t),{cc}_i^{(\mathcal{T})}(t),{\tilde{\beta }}_i(t)\right]={\text{MLP}}_{{\theta }_3}(zz(t),{ll}_i^{(\mathcal{T})})$$
由于静态网络与瞬时网络在前端具有重合部分，则可以将重合部分提取出来，$[\sigma (t),zz(t)]={\text{MLP}}_{{\theta }_1}({\gamma }_{xx}(rr(t)))$，根据文章的描述，最后构建出完整的NeRF-W网络结构，如下图所示：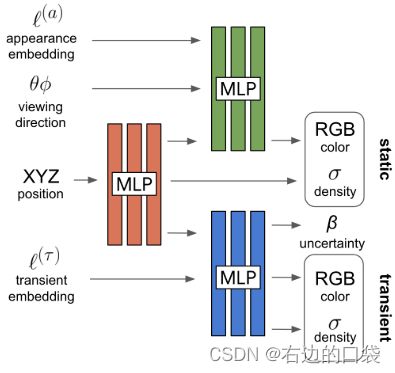

模型优化

定义图像$i$中的光线$rr$的颜色信息${CC}_i(rr)$的loss为：$$L_i(rr)=\frac{||{CC}_i(rr)-{\widehat{CC}}_i(rr)|{|}_2^2}{2{\beta }_i(rr{)}^2}+\frac{log{\beta }_i(rr{)}^2}{2}+\frac{{\lambda }_u}{K}\sum _{k=1}^K{\sigma }_i^{(\mathcal{T})}(t_k)$$前两项是${CC}_i(rr)$相对于均值${\widehat{CC}}_i(rr)$和方差${\beta }_i(rr{)}^2$的正态分布的（平移后的）负对数似然估计。${\beta }_i(rr)$值越大，赋值给像素的重要性就越小。第三项是$L_1$正则项，有一个非负的乘法系数${\lambda }_u$乘在瞬态${\sigma }_i^{(\mathcal{T})}$上面，这会鼓励模型使用瞬态不透明度来解释静态现象。在测试期间，我们会扔掉瞬态和不确定场，只渲染$\sigma (t)$和$cc(t)$，下图是NeRF-W网络的几个重要结果：

最后定义损失函数：$$\sum _{ij}{L}_i({rr}_{ij})+\frac{1}{2}||CC({rr}_{ij})-{\widehat{CC}}_i^c({rr}_{ij})|{|}_2^2$$

结果展示

参考文献和资料

[1]【论文精炼】 | NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections | NeRF in the Wild: 无约束照片集的神经辐射场 | 2021年
[2]NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections不受约束的照片集
[3]NeRF-W原文
[4]NeRF-W官网