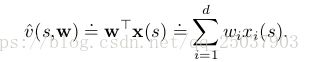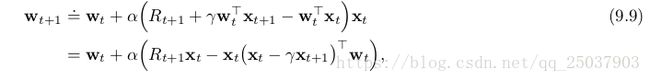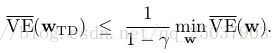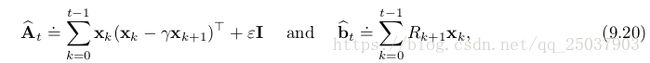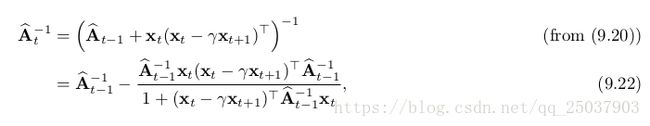强化学习（RLAI）读书笔记第九章On-policy Prediction with Approximation

这一章学习使用on-policy的数据对状态值函数进行逼近，也就是在策略下估计值函数。这一章的重点在于估计的值函数不是使用表格来表示而是使用参数w的函数形式。一般来说权重参数的数量是远远比状态的数量要小的，而且改变一个权重的大小会影响到很多个状态值的估计。于是一个值函数的更新会带来很多其它值函数的改变。这种泛化能力非常有用但更难操作和理解。

而且把强化学习延伸到函数逼近的形式也使得它能够应用于部分可观测的问题，也就是agent的部分状态是无法观察到的。实际上本章所讲的很多理论和方法都可以应用到部分观测的问题里。但是函数逼近不能够使用以往观测的记忆来改进当前状态表示。

9.1 Value-function Approximation

本书中讲到的所有预测方法都被描述为把特定状态的值函数估计朝着一个backup值变化的过程，这个backup值也叫作update target。很自然地把每个更新过程看作是值函数对于特定输入输出行为的一个例子。实际更新的过程很简单：其它状态的值函数都不变，当前状态的值函数向着目标值变动一个小部分。现在我们允许使用任意的复杂函数来完成这个更新的过程，并且在状态s的更新也会导致其它很多状态值的变化。通过这种方式来学习模仿输入输出样例的机器学习方法通常叫做监督学习，当输出是一个数字时一般叫做函数逼近。函数逼近希望能够收到它所期望模仿的函数的输入输出样例。然后我们把得到的近似函数叫做估计值函数。

把每次更新都看成一个传统的训练样例能够使我们能够应用很多现有的值函数逼近方法。理论上我们可以使用所有监督学习的方法，包括神经网络、决策树和其它很多多变量的回归函数。在强化学习中，能够在agent与环境进行交互的同时进行在线学习是一个很重要的要求。因此需要能够从增量式的数据中进行学习。而且强化学习还要求函数逼近能够解决非稳态目标函数。

 

9.2 The Prediction Objective (  )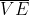

在表格形式的值函数计算里不需要一个评估估计质量的值因为学到的值函数就是精确收敛到真正的值函数的。但是在值函数的逼近中，一个状态的更新会影响很多其它状态，因此不可能精确得到所有的状态值函数。因为我们假设状态的数量远大于参数的数量，因此让一个状态的估计值更精确意味着很多状态的估计值更不精确。因此需要明确哪些状态是我们更加关注的。因此有一个根据状态的分布，代表的是每个状态的重要性。因此根据每个估计值和真正的状态值之间的平方差的加权和得到了我们的目标函数均方误差函数，用表示：

这个值的平方根给出了对于每个估计值与真值之间的误差。一般来讲选择的是在每个状态上花费的时间占比。对于on-policy的情况这个分布叫做on-policy分布也就是本章考虑的内容。对于continuing tasks，on-policy分布一般是在策略下的固定分布。

continuing tasks和episodic tasks虽然行为很相似，但是在值逼近中必须在正式分析中将它们分开看。也就是目标函数具体实现的不同。

目前来说还不清楚上述目标函数就是对于强化学习最适合的目标函数。因为我们的最终目标是找到最优的策略。而对应的最优的值函数不一定就是最小化VE。不过目前为止还没找到更好的替代函数，所以还是集中在VE上。

对于优化目标函数来说最好的是得到一个全局最优的权重，但是一般来说复杂函数很难收敛到全局最优，因此经常会收敛到局部最优。对于非线性函数来说，收敛到局部最优也不能完全保证，但是通常这样就够了。同样对于很多强化学习的例子中也不能保证收敛到极值或者极值的一个范围内。有些方法实际上是发散的。

 

9.3 Stochastic-gradient and Semi-gradient Methods

这节讲解一个具体的使用随机梯度下降来进行函数逼近的方法。

在梯度下降法中参数是一个列向量，有固定数量的实数值，，用来逼近的值函数是。每一个离散时刻进行一次参数的更新，因此每一步的参数为。需要记住的是，没有一组参数可以在所有的状态上得到精确解，甚至都不可能在所有的样本上达到完全一致。同时还需要考虑对于那些没出现过的状态的泛化。

假设所有出现的样本都是在同一个分布下产生的，在这些样本的基础上进行最小化均方误差。随机梯度下降法对于每一个出现的样本都进行一次参数的更新：

这个梯度下降法叫做随机的原因在于每一次只对一个样本的结果进行更新，而这个样本是随机选择的。

因为我们算法的目标不是在所有的状态值函数上都达到0误差，而只是得到一个近似函数能够平衡不同状态值函数的误差。因此每一次的更新都只进行一小步的更新，也就是步长参数会很小。而且还会假设步长会随着时间逐渐减小。如果它满足书中公式2.7的情况，那么这个方法能够保证结果收敛至一个局部极小值。

现在考虑一下目标输出值，也就是状态值的一个随机逼近。因为我们无法知道每个状态的精确值，因此没法进行精确地像公式（9.5）中的更新，只能使用替换真值。因此实际中随机梯度下降法的更新公式为：

只要估计值是真值的无偏估计，那么在步长参数满足2.7的情况下参数保证收敛至局部最优值。

如果目标值的估计中使用了自举的话就没法像9.7式中一样有收敛性保证。可以看到从9.4式到9.5的推导是基于括号中前一项与系数无关而得到的。但是使用了自举来作为前一项的估计，那么前一项就是与系数有关的。因此此时的更新只计算了一部分的梯度，所以这个方法叫做半梯度法。

尽管半梯度法不像梯度法一样健壮地收敛，但是在一些重要的应用中比如下一节的线性情况它依然收敛。而且，因为一些优点这个方法会被优先选择。一是这个方法一般会收敛得明显更快。二是这种方法可以进行连续而在线的学习，不如要等待一个episode结束。算法如下：

 

9.4 Linear Methods

函数逼近的一个最重要的例子是近似函数作为系数w的线性函数。线性近似方法中，状态值近似函数是和之间的内积：

 

其中向量x(s)叫做状态s的特征向量。对于线性方法来说，特征是奇函数，因为特征组成了近似函数的线性基的集合。对于线性方法来说使用SGD方法是很自然的。对应9.7的系数更新公式为：

因为它的简单，线性SGD法是最适合用来数学分析的。特别的是，线性方法中极值只有一个，因此任何保证能够收敛至局部最优的方法会自动保证收敛至全局最优。上节中介绍的半梯度法TD(0)算法同样会在线性函数逼近中收敛，不过这是根据SGD的另一个特性。对于每一步的系数迭代为：

可以写为另外的形式：

可以看出当系数收敛的时候

这个值叫做TD不动点。实际上半梯度法TD(0)收敛到这个点。而且这个点的存在和A的可逆在书上有证明。

在不动点上，目标函数被证明在一个值范围以内：

也就是TD法得到的误差不会比MC法的最小误差大倍。因为TD法之前讲过，方差更小而且收敛得更快，因此选用哪个方法要考虑近似和问题本身以及学习过程的长短。还有一些其它on-policy的自举方法也会收敛到相似的上限。比如线性半梯度法DP也收敛到TD不动点。半梯度法Sarsa(0)算法收敛至相似的点与相似的上限。对于episodic tasks有一些不同但是相关的上限。对于这些收敛结果来说最重要的一点是这些状态是根据on-policy分布来更新的。

半梯度法n步TD算法的伪代码如下：

练习9.1  系数为全为1的列向量。特征为对应状态的值函数，其他状态为0。

 

9.5 Feature Construction for Linear Methods

线性方法不仅仅因为能够保证收敛而有趣，更是因为在实际应用中能够对于数据和计算都很有效率。对于特定的问题，选择合适的特征向量是一个重要的对强化学习系统添加先验的方法。线性方法的一大局限是它不能够考虑进不同特征之间的交互，比如有的特征i只有在与j同时出现的时候才比较有效。

9.5.1 Polynomials

很多问题中，强化学习的函数逼近和很多插值和回归很像。多项式能够组成用来插值和回归的最简单的一组特征。

比如当前问题的状态有两个数字维度，那么对于每个状态来说可以使用这两个数字(s1,s2)表示。如果直接把他们当做状态的特征那么，但是这样就不能够体现出这两个维度之间的交互。而且如果这两个数字都是0，那么这个估计值也会是0。这两个限制都可以使用这个四维特征来克服。其中第一个1可以允许对初始状态数字的仿射函数，而最后一项两个数的乘积，考虑进了两个维度的交互。也可以选择一个含有更高维特征的特征向量。一般化这种选择特征的方式，我们可以得到使用多项式的特征，构成方式如下：

但是由于特征的数量会随着维度k呈指数增长，所以只需要选择其中一部分用来做函数逼近。

练习9.2 可以充分保证不同维度之间进行充分的交互，以及特征1用作原状态特征的仿射。

练习9.3  2 4

9.5.2 Fourier Basis

另一个使用线性近似函数的方法是使用傅里叶序列，也就是把时序函数表示成不同频率的sine基函数和cosine基函数的加权和的形式。在强化学习中，需要逼近的函数是未知的，使用傅里叶基因为用起来很简单而且能够在一些了强化学习问题中表现得很好。

（作为一名通信本科的学生我没有看懂它怎么弄得，算了，我有罪。）

9.5.3 Coarse Coding

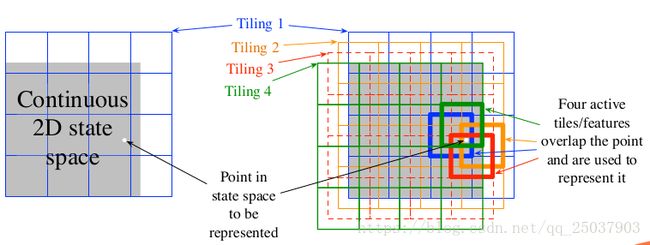
现在考虑任务是在一个自然连续的二维空间中。其中一种表示这种情况的特征是对于空间中对应圆的表示，如右图。如果一个状态是在圆中，那么该圆对应的特征值应该是1，表示present；否则应该是0表示absent。这种1-0的特征叫做二维特征。对于一个给定的状态，每个而为特征表示的是这个状态是否在这个圆中，于是就粗编码了这个位置。把状态通过这样的重叠的特征来表示的方法叫做粗编码。

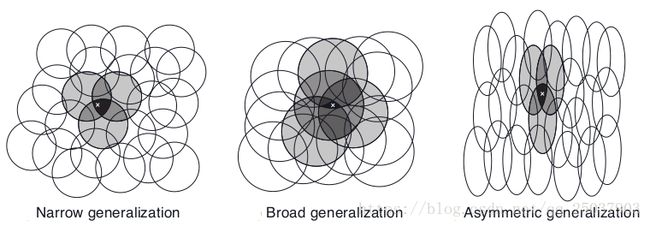
假设在线性梯度下降函数逼近中，考虑圆的大小和密度。对应每个圆的是会被学习算法影响的参数。如果我们训练一个在某个圆中的状态，那么所有的在这个圆中的其它状态都会受到影响。因此对于圆比较小的情况，每个点的影响距离就比较小，而对于比较大的圆影响就比较大。而且圆的形状也决定了泛化的特性。如下图所示：

9.5.4 Tile Coding

tile coding是对于高维连续空间的一种灵活高效的coarse coding。在tile coding中每个特征的接受范围被划分成一个个状态空间的分隔。比如在最简单的二维空间中使用一个均匀分布的网格。这个网格是正方形的，只使用一个网格，那么白色点可以被它落在的格子来表示。泛化会应用到格子中和格子外的所有状态。只用一个网格我们没有做到粗编码而只是一个状态聚集。

为了得到粗编码，我们需要对接收区域进行重叠，而且不能有完全重复的网格。上图中展示了使用四个网格的形式。每个状态，比如上右图中的白点，在四个网格中都落入了每个网格中的一个格子里。而这个特征向量对于每个网格的每个格子都有一个分量。因此在这个例子里有4x4x4=64个分量，除了落进去的4个格子，其它每个格子对应的分量都是0。

tile coding的一个快速的实用好处在于，因为是使用的对于空间的划分作为网格，因此对于每个状态来说，每次活跃的特征分量个数和网格数一样，因为每个网格中只有一个格子被激活。这样也可以简单的设置步长为网格数的倒数，可以带来精确地one-trial learning。

同样由于使用了二维特征，tile coding可以获得一定的计算优势。特征都是0和1，因此相加的时候非常快速。

对于其它状态而言，当前状态更新的时候受影响的程度和与当前状态有共享格子的个数有关。

在选择网格策略的时候，需要选择网格的数量和格子的形状。网格的数量决定了近似的精准度。而每个网格的形状决定了泛化的特点。方格对于每个维度相同看待，而沿着一个维度逐渐拉长的网格会增加那个维度的泛化性。而对角斜纹网格会增加对角线维度的泛化性。实际应用中经常需要在不同的网格中使用不同形状的格子。网格的选择决定了泛化性能，直到网格能够被自动化选择之前，选择更灵活而且对人类更有意义的网格很重要。

还有一种减少内存消耗的方式是哈希。

练习9.4 在一个维度上网格逐渐扩大，在另一维度等分。

9.5.5 Radial Basis Functions

RBFs是对于粗编码对于连续值特征的自然拓展。相对于只能是0或1的特征，RBFs特征可以是0-1之间任意的数字。经典的RBF特征作为一个高斯形式的反馈，只依赖于状态s与设定好的中心状态之间的距离以及特征的相对宽度:

使用RBFs相对于0-1特征的最原始的优点是它可以使得近似函数更加平滑而且可微。尽管很诱人但是实际上经常没有实用性。

9.6 Selecting Step-Size Parameters Mannually

大多数SGD方法需要手动选择步长参数。理论思考很不幸的没有多大帮助。使用2.7的收敛条件可以保证收敛，但是这种情况下学习的速度太慢。在表格MC方法中设计的不适应TD方法或者非稳态问题或者任意的函数逼近方法。对于线性方法，有一种递归的最小方差的方差来设定一个步长矩阵，这些方法可以延伸为一个差分学习方法叫做LSTD。因为复杂度的问题我们不在最需要函数逼近的大型问题中使用这些方法。

在表格型方法中，设定来使得表格估计值利用最近步的估计值来逼近目标的均值。但是在大部分函数逼近的方法中，并没有这么清楚的每个状态经验的数量，因为每个状态都可能与其它状态在某些地方相似或不相似。但是在线性函数逼近中依然有一个相似的规则给出相似的行为。假设想要学习一个有相同特征向量的状态个经验值，那么应该设定线性SGD算法的步长为

这个方法在特征向量长度不变的时候效果最好，理想状态是为常数。

练习9.5  

9.7 Nonlinear Frnction Approximation: Artificial Neural Networks

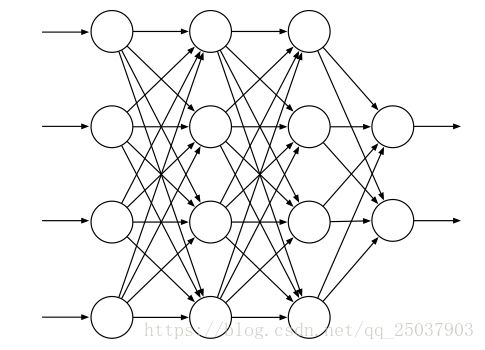
ANN是一个拥有一些神经元特性的单元连接起来的网络。第十六章介绍一些在强化学习系统中使用ANN进行函数逼近得到良好结果的例子。下图展示了一个简单的前馈神经网络。

每个单元一般是半线性的单元，意味着他们是输入的甲醛和然后在结果上应用一个非线性函数，叫做激活函数，来得到一个单元的输出，或者激活。一般使用的激活函数有sigmoid和rectifier。一个没有隐藏层的ANN只能表示很小一部分可能的输入输出函数。但是一个只有一层隐藏层但是有足够多的有限数量sigmoid单元的ANN可以在网络的输入空间上逼近输入任何连续函数到任意精度。但是如果所有的激活函数都是线性的，那么ANN等同于一个没有隐藏层的网络结构。

尽管一层隐藏层就可以逼近任何函数，但是依然选择使用多层级联的形式构成有多个隐藏层深度神经网络。越靠近输出层的隐藏层计算的输入表示就相对越抽象，而每个隐藏层单元都为整个输入输出函数的网络提供了一个层次的特征表示。因此训练一个ANN的隐藏层就相当于是对给定的问题自动的训练特征，而不需要完全依赖手动构造的特征。在大部分的监督学习里，目标函数是一个在一堆有标记的训练样本上期望的偏差或者损失函数。但是在强化学习里，ANN可以使用TD误差来学习值函数，或者可以最大化期望反馈或者进行策略梯度算法。

使用ANN最成功的算法是backpropagation算法。但是bp算法对于浅层网络效果很好，对于深层网络效果不太好。实际上训练k+1层网络一般会比训练k层网络得到的效果更差。原因在于，第一，深层网络的大规模的参数使得其很容易overfitting。第二，bp算法对于深层网络效果不好，因为随着深度加深，梯度回传至前面的隐藏层的时候，梯度的变化由于练成会变得太小或者太大都不能得到较好的效果。

过拟合在在线强化学习问题里不那么明显因为它并不是依赖于一个有限的训练集。但是过拟合对于ANN来说是一个很大的问题因为深度网络有非常多的参数，有几种方法可以缓和。一、当验证集上效果开始下降时停止训练。二、调整目标函数来抑制拟合的复杂性。三、通过增加权重之间的依赖性来减少自由度。还有一个特别有效的方法叫做dropout。指的是在训练的过程中随机的移除网络中的某些单元。这样就相当于在网络中训练了很多个更小的网络并且综合它们的效果。这个方法需要每个隐藏层单元学习出能够与其它特征随机集合都能有较好效果的特征，因此避免了其对于特殊样例的过拟合。

还有一种解决训练深层网络问题的方法是使用deep brief networks，不懂跳过。

batch normalization是让训练深层ANN更加简单的另一种技术。batch normalization在神经网络中对于每一个隐藏层的输出进入下一层之前都进行归一化。

还有个技术叫做deep residual learning。不懂跳过。

还有一种deep ANN叫做深度卷积网络。应用在图像领域很多，16章会讲很多相关的样例。

上面讲到的很多ANN的设计和训练方法，都能够应用到强化学习的使用中。尽管目前强化学习理论大部分局限于表格型和线性函数逼近的方法，但是著名的强化学习应用的惊人性能很多都来自于多层ANN来进行非线性函数逼近的成功应用。

 

9.8 Least-Squares TD

这章目前讲的都是需要在每一个时间步骤进行正比于参数数量复杂度的计算。但是如果进行更多计算，算法会得到更好结果。这节介绍一个对于线性函数近似可论证是最优的方法。

9.4节讲到了线性函数逼近的TD(0)算法会渐进收敛至TD不动点，其中。进行每步迭代计算是不必要的，可以使用一个更直接的方式来计算不动点，就是LSTD算法。其中

是一个很小的正数，用来保证A是可逆的。理论上讲还需要除以时间t，但是在进行计算的时候分子分母可以抵消因此不需要。可以直接计算系数为。

这个算法相比线性TD(0)法更充分利用了数据，但是需要更多的计算量。半梯度法TD(0)中每个时间步骤的计算复杂度是。在LSTD算法中，A和b的估计值可以使用增量形式在常数时间内完成，但是A的更新需要计算一个外积，复杂度是，空间复杂度也是这样。而且对A求逆才是最耗时间的，时间复杂度是。幸运的是A的逆是一个特殊形式，可以使用增量式写法，只需要复杂度的计算：

看起来很复杂，但实际上只包含了向量矩阵乘法和向量之间的乘法，因此时间复杂度是，空间复杂度也是。

当然这个时间复杂度依然是非常大的消耗，但是算法对于数据的高效利用是值得这个计算消耗的。LSTD算法不需要步长参数，这一点经常被吹捧，但是却需要一个。太小，求逆的结果可能会变化很大，太大学习的速度就会很慢。而且没有步长意味着LSTD算法不会遗忘，有时候这一点是需要的。在control算法中LSTD法需要结合其它的机制来引入遗忘，使得不需要步长的优点毫无意义。

9.9 Memory based Function Approximation

我们目前讲的都是参数化的方法来逼近值函数。但是基于记忆的方式不同，它们只需要保存算法访问过的训练样本（的一部分）而不需要更新任何参数。当需要查询某个状态的值估计的时候，利用记忆中的过往样本来计算出这个状态的值即可。这个方式有时也叫作lazy learning因为知道系统需要输出时才对训练样本进行处理。

和参数化方法不同，基于记忆的方法的近似函数并不局限于一类固定参数的函数，而是有训练样本来决定。通过组合过往的训练样本来输出查询状态的状态值。训练样本越多，非参数化方法的结果就越精确。

有很多种基于记忆的算法。我们关注一种local-learning的算法。这些算法通过利用查询状态附近的邻居来逼近值函数。从样本中先提取出和查询状态相近的样本，然后可以根据距离赋予权重，之后组合这些邻近样本给出查询结果。结果随后丢弃。最简单的基于记忆的方式叫做最近邻居法。就是直接返回和需要查询的状态最接近的状态的结果。稍微复杂点的方式就是抽取一堆比较邻近的样本，然后输出他们的加权平均。locally weighted regression也是类似，只不过是在附近的状态集合上拟合出一个平面来得到结果。之后这个平面也会被丢弃。

作为非参数化的方法，基于记忆的算法相对参数化方法有很多优点。比如随着数据增多，精准度会越来越高。而且非参数法可以更适应强化学习算法。比如在Trajectory sampling中，非参数化的结果可以更关注那些真实轨迹中访问过的状态。而且非参数法可以使得样本对于邻近状态的影响更直接，而不像参数法那样需要增量式调整参数来得到全局近似。

避免全局近似也是一个解决维度灾难的好方法。非参数法存储n个样本只需要正比于n的空间，但是对于有k维的样本空间，参数法需要解决指数级的参数或者状态空间。当然还有个关注点就是非参数法是否能够快速相应对状态的查询。在一个很大的数据集中查询最邻近节点需要太长的时间。

使用并行计算可以加速最邻近节点的查询，特殊的多维数据结构如kd树就是个快速查询的例子。locally weighted regression额外需要找到快速计算回归的方式。

 

9.10 Kernel-based Function Approximation

上节讲的基于记忆的加权平均和加权回归法都依赖于对于两个状态之间赋予一个权重的算法。这个赋予权重的函数叫做核函数，或者叫做一个核。稍微不同的看待的话，核函数是计算从s’到s泛化能力的计算。核函数计算出任何两个状态之间关联知识程度的数值表达。

kernel regression是一个计算记忆中所有样本核加权平均然后将结果赋值给查询状态的基于记忆的方法。

一个常用的核叫做高斯射线基函数（RBF），和RBF函数逼近用到的一样。函数逼近的形式是一个预先定义的RBFs的线性组合。每个基的参数可以通过SGD的方法进行学习。但是使用RBF核函数的kernel regression不一样，首先它是基于记忆的：RBF是以存储过的样例状态为中心的。第二：它是非参数化的：没有参数需要学习，只需要给出一个查询反馈。

任何线性参数回归的方法，比如9.4中讲的那种把状态表示为一个特征向量形式的，都可以重写为kernel regression的形式，其中核函数k(s,s')是特征向量的内积，也就是。重写为kernel regression的线性参数方法如果使用同样的学习样本会得到相同的结果。

我们可以直接构造核函数而不需要考虑任何的特征向量。不是所有的核函数都能够表示为特征向量的内积，但是那些可以表现为特征向量内积的核函数能够提供相对参数方法更重要的优势。很多特征向量有一个更加简洁的函数形式而不需要在一个d维空间中进行计算。在这些例子里，kernel regression比直接使用这些特征向量的线性参数表示更简单。这叫做核技巧，能够更高效的基于已知训练样本在高维的高消耗的特征空间中计算。这是很多机器学习方法的基础。

 

9.11 Looking Deeper at On-policy Learning: Interest and Emphasis

目前讲到的算法都把每个遇到的状态都平等看待，就像它们是一样重要一样。但是有些例子里我们更关注某些特定的状态。比如在discounted episodic的问题里，我们可能更关注更早访问的状态的值，因为后面状态的值被设置的很小。函数逼近的计算力是有限的，因此我们需要更加关注那些能够有效提高性能的状态。

我们把目前遇到的状态都平等看待的一个原因是我们目前根据on-policy分布进行更新。在这个分布上能够得到半梯度法更强的理论结果。现在介绍几个新概念。一个是介绍一个非负的标量值，叫做interest的一个随机变量，代表的是在时间t时我们关注当前状态的程度。于是9.1节中的均方误差函数VE中的分布就定义为根据遵循当前目标策略下遇到状态的分布根据Interest加权得到的结果。第二定义另一个非负的标量随机变量，emphasis 。这个标量乘以每次更新时候的误差来表示对这次学习的重视程度。比如n步更新可以写为：

其中emphasis的定义为：

 

9.12 Summary

如果想要强化学习能够应用到AI或者大型的更称应用中，强化学习就必须有足够的泛化能力。为了达到这个目的，目前的监督学习方法都可以将每次更新看做一个样本来作为监督学习的函数逼近。

最适合的监督学习方法可能是使用参数的函数逼近。其中策略被参数化为权重向量w。定义了均方误差函数作为函数逼近的衡量方式。为了找到更合适的权重向量，最流行的方式是随机梯度下降法。这章关注on-policy基于一个固定策略的形式，叫做prediction或者evaluation。在这种形式里最自然的算法是n步半梯度TD法，它包含了MC和半梯度TD(0)。

使用半梯度法可以在线性函数逼近中得到很好的结果。线性函数逼近的结果就是特征向量的参数加权和。线性情况有很好的理论研究结果。特征向量的选择是一个非常重要的往强化学习中添加先验的形式。主要方法有多项式法（在在线学习力泛化能力差），傅里叶基（需要重复分隔范围的粗编码），tile coding法和Radial basis函数法。LSTD算法是一个最有效的线性TD预测算法，不过需要平方级别的计算复杂度。非线性方法比如神经网络在最近几年通过深度强化学习的方式也变得很火。

线性半梯度n步TD算法保证收敛至一个最优误差的范围内。n越大误差越小。但是更大的n会使得学习更慢，因此实际中一定程度的自举会更好。