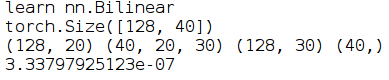pytorch中的nn.Bilinear

参考：pytorch中的nn.Bilinear的计算原理详解

代码实现

使用numpy实现Bilinear（来自参考资料）：

print('learn nn.Bilinear')
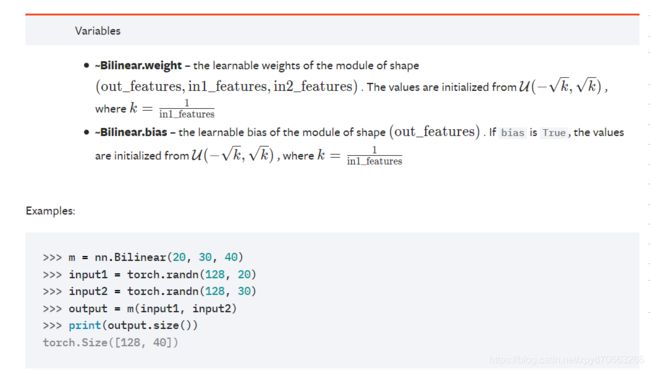
m = nn.Bilinear(20, 30, 40)
input1 = torch.randn(128, 20)
input2 = torch.randn(128, 30)
output = m(input1, input2)
print(output.size())
arr_output = output.data.cpu().numpy()
 
weight = m.weight.data.cpu().numpy()
bias = m.bias.data.cpu().numpy()
x1 = input1.data.cpu().numpy()
x2 = input2.data.cpu().numpy()
print(x1.shape,weight.shape,x2.shape,bias.shape)
y = np.zeros((x1.shape[0],weight.shape[0]))
for k in range(weight.shape[0]):
    buff = np.dot(x1, weight[k])
    buff = buff * x2
    buff = np.sum(buff,axis=1)
    y[:,k] = buff
y += bias
dif = y - arr_output
print(np.mean(np.abs(dif.flatten())))

输出结果：

可以看到我们自己用numpy实现的Bilinear跟调用pytorch的Bilinear的输出结果的误差在小数点后7位，通过编写这个程序，现在可以理解Bilinear的计算过程了。需要注意的是Bilinear的weight是一个3维矩阵，这是跟nn.linear的一个最大区别。

首先，以weight的第0维开始，逐个遍历weight的每一页，当遍历到第k页时，输入x1与weight[k,:,:]做矩阵乘法得到buff，然后buff与输入x2做矩阵点乘得到新的buff，接下来对buff在第1个维度，即按行求和得到新的buff，这时把buff的值赋值给输出y的第k列

遍历完weight的每一页之后，加上偏置项，这时候Bilinear的计算就完成了。为了检验编写的numpy程序是否正确，我们把输出y跟调用pytorch的nn.Bilinear得到的输出output转成numpy形式的arr_output做误差比较。

公式

设 $X_1$ 形状为 $[batch\_size,inpu{t}_1]$，$X_2$ 形状为 $[batch\_size,inpu{t}_2]$

nn.Bilinear 内部的参数形状为：

参数 $W:[output,inpu{t}_1,inpu{t}_2]$，令 $W_k=W[k,:,:],1\le k\le output$，其形状为 $[inpu{t}_1,inpu{t}_2]$ ;

参数 $b:[output]$

下述代码使用nn.Bilinear得到 $Y$，其形状为 $[batch\_size,output]$。

m=nn.Bilinear(input_1,input_2,output)
Y=m(X_1,X_2)

实际计算公式使用python语法可以表达为：

$$Y=concatenate([sum(X_1{W}_k\odot X_2,axis=1)for{W}_{k}inW],axis=1)+b$$

其中$X_1$与$W_k$之间使用矩阵乘法，其结果与 $X_2$ 使用逐元素乘法；

$sum(tensor,axis=1)$ 表示将在轴 1 方向上求和进行归约（维度减一）。

$concatenate(list\_of\_tensor,axis=1)$ 表示将多个tensor在轴 1 方向上进行拼接。

最后的加法为广播加法，因为加号左边维度为$[batch\_size,output]$，而右边为 $[output]$