机器学习算法 - 神经网络
文章目录
- 一、非线性假设
- 二、感知机与多层网络
-
- 2.1感知机
- 2.2多层网络
- 三、前向传播算法
- 四、神经网络模型展示
-
- 4.1单层神经网络模拟逻辑与、或
- 4.2多层神经网络模拟同或(异或非)
- 五、神经网络的代价函数
- 六、最小化代价函数 - 反向传播算法
-
- 6.1回顾前向传播
- 6.2反向传播的意义
- 梯度计算
- 链式法则
- 公式推导
- 6.3反向传播示例
-
- 误差公式解析
一、非线性假设
我们之前已经学习过线性回归和逻辑回归算法了,为什么还要研究神经网络? 我们先看一个例子。下面是一个监督学习分类问题的训练集。
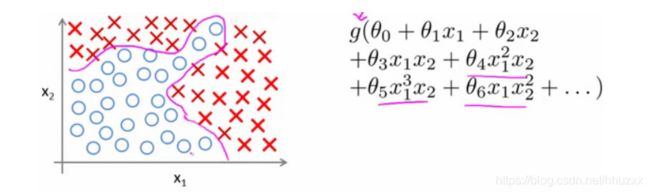
当我们使用x1,x2的多次项式进行预测时,我们可以应用的很好。 使用非线性的多项式项,能够建立更好的分类模型。假设有非常多的特征,例如大于100个变量,希望用这100个特征来构建一个非线性的多项式模型,结果将是数量非常惊人的特征组合,即便只采用两两特征的组合,也会有接近5000个组合而成的特征。这对于一般的逻辑回归来说需要计算的特征太多了。
普通的逻辑回归模型,不能有效地处理这么多的特征,这时候就需要神经网络模型。
二、感知机与多层网络
神经网络模型建立在很多神经元之上,每个神经元是一个学习模型。这些神经元(也叫激活单元,activation unit)采纳一些特征作为输入,并且根据本身的模型提供一个输出。
神经元接收来自其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过”激活函数“处理以产生神经元的输出。实际常用Sigmoid函数作为激活函数。(引用西瓜书上的原话)
2.1感知机
感知机(Perceptron)由两层神经元组成。输入层接收外界输入信号后传递给输出层,输出层是M-P神经元(亦称”阈值逻辑单元“(threshold logic unit))。
注意:
感知机只有输出层神经元进行激活函数处理,即只拥有一层功能神经元,学习能力有限。
感知机只能解决线性可分问题
2.2多层网络
要解决非线性可分问题,需要多层感知机,就是多层网络。
输入层和输出层之间的层称为”隐层“或”隐含层“,隐含层和输出层都是拥有激活函数的功能神经元。
在神经网络中,只需包含隐层,即可称为多层网络。
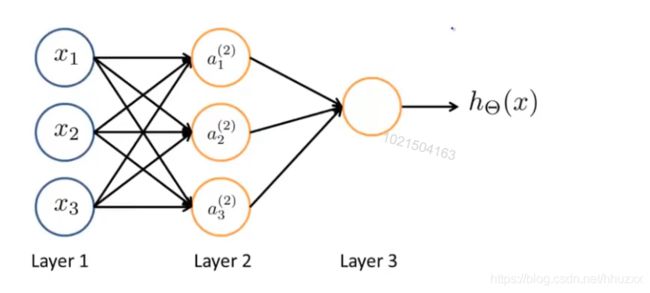
其中: x 1 , x 2 , x 3 \small x_{1},x_{2},x_{3} x1,x2,x3 是输入单元,将原始数据输入给它们,处于输入层; a 1 , a 2 , a 3 \small a_{1},a_{2},a_{3} a1,a2,a3是中间单元,负责将数据进行处理,然后呈递到下一层;最后是输出单元,它负责计算 h θ ( x ) \small h_{\theta}(x) hθ(x)。
标记:
L L L:表示神经网络层数
S L S_L SL:表示第L层的单元数(不包括偏置单元)
a i ( j ) a_i^{(j)} ai(j):第 j \small j j层的第 i \small i i个单元的激活值
θ ( j ) \theta^{(j)} θ(j):从第 j \small j j层映射到第 j + 1 \small j+1 j+1层的权重矩阵
k k k:表示输出的类别数,相当于输出单元数
说明:
当类别k=2时,则直接用一个输出单元
当类别k>=3时,就有k个输出单元。 S L = k S_L=k SL=k
三、前向传播算法
下图为一个3层的神经网络,第一层为输入层(Input Layer),最后一层为输出层(Output Layer),中间一层为隐藏层(Hidden Layers)。我们为每一层都增加一个偏差单位(bias unit)。
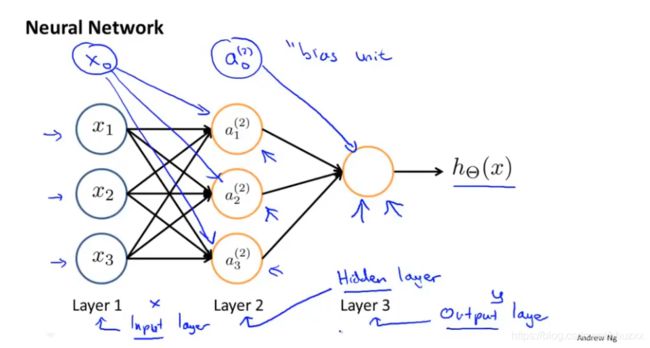
标记:
a i ( j ) \small a_i^{(j)} ai(j):第 j \small j j层的第 i \small i i个单元的激活值
θ ( j ) \small \theta^{(j)} θ(j):从第 j \small j j层映射到第 j + 1 \small j+1 j+1层的权重矩阵;例如 θ ( 1 ) \small \theta^{(1)} θ(1)代表从第1层映射到第2层的权重矩阵,其大小为:第 j + 1 \small j+1 j+1层的激活单元数量为行数,以第 j \small j j层的激活单元数加1为列数的矩阵。
对上述模型,激活单元和输出分别表达为:
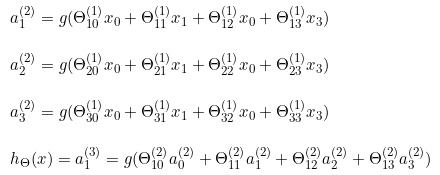
把 x , θ , a x,\theta,a x,θ,a 分别用矩阵表示:

可得 Θ ⋅ x = a \Theta \cdot x=a Θ⋅x=a
把这样从左到右的算法称为前向传播算法( Forward Propagation )
说明:
此处 θ ( 1 ) ∈ R 3 × 4 \theta^{(1)}\in R^{3\times4} θ(1)∈R3×4 ,属于 3 × 4 3\times4 3×4的向量
更一般的,如果一个网络在第 j j j层有 S j S_j Sj个单元,那么矩阵 θ ( j ) \theta^{(j)} θ(j)的维度为 S j + 1 × ( S j + 1 ) S_{j+1} \times (S_j+1) Sj+1×(Sj+1),这里包含了偏置单元
四、神经网络模型展示
介绍神经网络模型的展示,实现不同的功能。此处假设 h Θ ( x ) = 1 1 + e − θ T X \small h_\Theta(x)=\frac{1}{1+e^{-\theta^TX}} hΘ(x)=1+e−θTX1
4.1单层神经网络模拟逻辑与、或
单层神经网络可以解决线性可分问题,比如逻辑与、或、非等。
举例说明:逻辑与(AND)
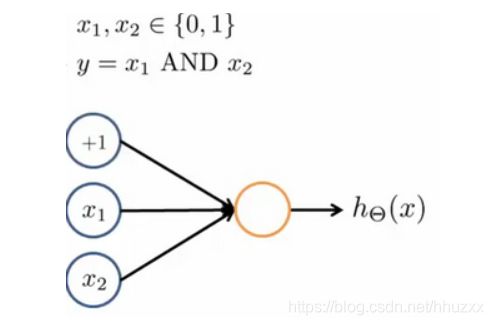
当 θ 0 = − 30 , θ 1 = 20 , θ 2 = 20 \theta_0=-30,\theta_1=20,\theta_2=20 θ0=−30,θ1=20,θ2=20,此时 h Θ ( x ) = g ( − 30 + 20 x 1 + 20 x 2 ) h_\Theta(x)=g(-30+20x_1+20x_2) hΘ(x)=g(−30+20x1+20x2)
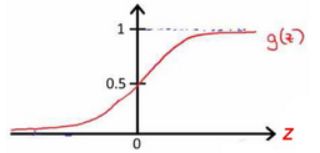

从图中可以看出 h Θ ( x ) ≈ x 1 A N D x 2 \small h_{\Theta}(x) \approx x_{1} AND \small x_{2} hΘ(x)≈x1ANDx2
4.2多层神经网络模拟同或(异或非)
多层功能神经元,解决非线性可分问题
举例说明:逻辑同或(XNOR)
XNOR = (x and y) or ((NOT x) and (NOT y))
x,y也可表示为下图中的 x 1 , x 2 x_1,x_2 x1,x2

这种方法可以逐渐构造出越来越复杂的函数,也能得到更加厉害的特征值。
五、神经网络的代价函数
以逻辑回归代价函数作为一般形式有
L o g i s t i c r e g r e s s i o n Logistic \ \ regression Logistic regression:
J ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) l o g h θ ( x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=-\frac{1}{m}\Biggl [\sum_{i=1}^my^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))\Biggl ]+\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2 J(θ)=−m1[i=1∑my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
可以这样理解,上述式子代表神经网络中一个输出单元的代价函数。
在逻辑回归中,我们只有一个输出变量,又称标量(scalar),也只有一个因变量,但
是在神经网络中,我们可以有很多输出变量,我们的ℎ()是一个维度为的向量,并且我们
训练集中的因变量也是同样维度的一个向量,因此我们的代价函数会比逻辑回归更加复杂一
些,为:
![]()
N e u r a l n e t w o r k Neural\ \ network Neural network:
J ( Θ ) = − 1 m [ ∑ i = 1 m ∑ k = 1 K y k ( i ) l o g ( h Θ ( x ( i ) ) ) k + ( 1 − y k ( i ) ) l o g ( 1 − ( h Θ ( x ( i ) ) ) k ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 S l ∑ j = 1 S l + 1 ( Θ j i ( l ) ) 2 J_{(\Theta)}=-\frac{1}{m}\Biggl [\sum_{i=1}^m\sum_{k=1}^{K}y_k^{(i)}log(h_\Theta(x^{(i)}))_k+(1-y_k^{(i)})log(1-(h_\Theta(x^{(i)}))_k)\Biggl ]+\frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{S_l}\sum_{j=1}^{S_{l+1}}(\Theta_{ji}^{(l)})^2 J(Θ)=−m1[i=1∑mk=1∑Kyk(i)log(hΘ(x(i)))k+(1−yk(i))log(1−(hΘ(x(i)))k)]+2mλl=1∑L−1i=1∑Slj=1∑Sl+1(Θji(l))2
解释:
L:表示神经网络层数
S l S_l Sl:表示第L层的单元数(不包括偏置单元)
K:表示输出层的单元数
j:表示权重矩阵的行数
正则化中的i:表示权重矩阵的列
这个看起来复杂很多的代价函数背后的思想还是一样的,我们希望通过代价函数来观察
算法预测的结果与真实情况的误差有多大,唯一不同的是,对于每一行特征,我们都会给出
个预测,基本上我们可以利用循环,对每一行特征都预测个不同结果,然后在利用循环
在个预测中选择可能性最高的一个,将其与中的实际数据进行比较。
正则化的那一项只是排除了每一层 θ 0 \theta_0 θ0后,每一层的矩阵的和。最里层的循环循环所
有的行(由 +1 层的激活单元数决定),循环则循环所有的列,由该层( S l S_l Sl层)的激活单
元数所决定。
六、最小化代价函数 - 反向传播算法
6.1回顾前向传播

为了计算偏导数,我们使用一种反向传播的算法。
假设训练集只有一个样本,记为(x,y)。
我们先用前向传播算法计算在给定输入的时候,假设函数是否会真的输出结果。
a ( 1 ) = x a^{(1)}=x a(1)=x ( a ( 1 ) \ \ \ \ (a^{(1)} (a(1)表示第一层的激活值)
z ( 2 ) = θ ( 1 ) a ( 1 ) z^{(2)}=\theta^{(1)}a^{(1)} z(2)=θ(1)a(1)
a ( 2 ) = g ( z ( 2 ) ) a^{(2)}=g(z^{(2)}) a(2)=g(z(2)) ( a d d a 0 ( 2 ) ) \ \ (add \ \ a_0^{(2)}) (add a0(2))
z ( 3 ) = θ ( 2 ) a ( 2 ) z^{(3)}=\theta^{(2)}a^{(2)} z(3)=θ(2)a(2)
a ( 3 ) = g ( z ( 3 ) ) a^{(3)}=g(z^{(3)}) a(3)=g(z(3)) ( a d d a 0 ( 3 ) ) \ \ (add \ \ a_0^{(3)}) (add a0(3))
z ( 4 ) = θ ( 3 ) a ( 3 ) z^{(4)}=\theta^{(3)}a^{(3)} z(4)=θ(3)a(3)
a ( 4 ) = h Θ ( x ) = g ( z ( 4 ) ) a^{(4)}=h_\Theta(x)=g(z^{(4)}) a(4)=hΘ(x)=g(z(4))
6.2反向传播的意义
反向传播算法是一种计算偏导数的方法。反向传播就是和之前正向传播算法相对应的,从神经网络模型的最后一层误差开始,逐层往前推导的,反向传播求误差,其实是求模型代价函数偏导 ∂ ∂ θ i j ( l ) J ( Θ ) \frac{\partial}{\partial\theta_{ij}^{(l)}}J(\Theta) ∂θij(l)∂J(Θ)的一种手段,意义就在于比正向传播算法更快速更高效地求出代价函数偏导,在实际模型训练过程中,能大大降低计算时间,使模型更快收敛。
梯度计算
链式法则
公式推导
6.3反向传播示例
为了计算偏导数,我们使用一种反向传播的算法。
反向传播的含义:把输出层(第四层)的误差反向传播到第三层,再反向传播到第二层。
根据数学证明,可以推出代价函数的偏导数的计算公式(下图中最下方的蓝色手写体)
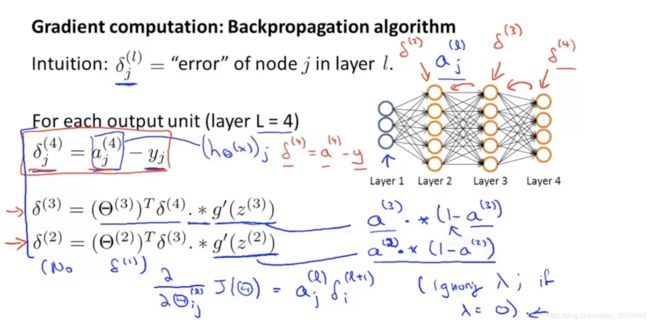
不考虑正则项,假设有m个样本,k项输出,我们从最后一层(输出层)的误差开始计算,假设误差用 δ \delta δ表示。 δ j ( l ) \delta_j^{(l)} δj(l)表示第 l l l层的第 j j j个单元的误差。
最后一层:误差 = 预测值 - 实际值 = δ j ( 4 ) = a j ( 4 ) − y j \delta_j^{(4)} = a_j^{(4)}-y_j δj(4)=aj(4)−yj ( a j ( 4 ) 也 可 写 成 ( h θ ( x ) ) j ) \ \ (a_j^{(4)}也可写成(h_\theta(x))_j) (aj(4)也可写成(hθ(x))j)
此图中:
第4层: δ ( 4 ) = a ( 4 ) − y \delta^{(4)}=a^{(4)}-y δ(4)=a(4)−y (向量表示)
第3层: δ ( 3 ) = ( θ ( 3 ) ) T δ ( 4 ) ⋅ ∗ g ′ ( z ( 3 ) ) \delta^{(3)}=(\theta^{(3)})^T\delta^{(4)}\cdot*g\prime(z^{(3)}) δ(3)=(θ(3))Tδ(4)⋅∗g′(z(3))
第2层: δ ( 2 ) = ( θ ( 2 ) ) T δ ( 3 ) ⋅ ∗ g ′ ( z ( 2 ) ) \delta^{(2)}=(\theta^{(2)})^T\delta^{(3)}\cdot*g\prime(z^{(2)}) δ(2)=(θ(2))Tδ(3)⋅∗g′(z(2))
第1层:No δ ( 1 ) \delta^{(1)} δ(1),因为第一层对应输入层,不存在误差
其中左半部分 ( θ ( 3 ) ) T δ ( 4 ) (\theta^{(3)})^T\delta^{(4)} (θ(3))Tδ(4)表示权重导致的误差的和;右半部分 g ′ ( z ( 3 ) ) g\prime(z^{(3)}) g′(z(3))是激活函数Sigmoid函数的导数。
具体的解析和推导见下面。
误差公式解析
参考资料:
https://zhuanlan.zhihu.com/p/74167352.
