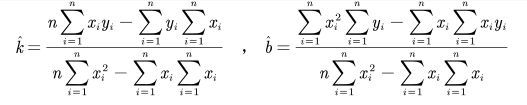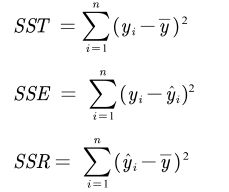数学建模常见的一些方法【04拟合算法】
文章目录
- 数学建模常见的一些方法
-
- 1. 拟合算法
-
- 1.1 插值和拟合的区别
- 1.2 求解最小二乘法
- 1.3 Matlab求解最小二乘
- 1.4 如何评价拟合的好坏
- 1.5 证明SST = SSE + SSR
- 1.6 计算拟合优度的代码
- 1.7 拟合工具箱
- 1.8 补充的计算函数randi,rand,normrnd,roundn
-
- 1.8.1 randi(范围,行,列): 产生均匀分布的随机整数(i = int)
- 1.8.2 rand(行,列): 产生0至1之间均匀分布的随机数
- 1.8.3 normrnd(均值,标准差,行,列):产生正态分布的随机数
- 1.8.4 roundn(数,位数)—任意位置四舍五入
数学建模常见的一些方法
1. 拟合算法
- 与插值问题不同,在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数(曲线),使得该曲线在某种准则下与所有的数据点最为接近,即曲线拟合的最好(最小化损失函数)。
1.1 插值和拟合的区别

插值算法中,得到的多项式f(x)要经过所有样本点。但是如果样本点太多,那么这个多项式次数过高,会造成龙格现象。
尽管我们可以选择分段的方法避免这种现象,但是更多时候我们更倾向于得到一个确定的曲线,尽管这条曲线不能经过每一个样本点,但只要保证误差足够小即可,这就是拟合的思想。(拟合的结果是得到一个确定的曲线)
1.2 求解最小二乘法
1.3 Matlab求解最小二乘
x =
4.2000
5.9000
2.7000
3.8000
3.8000
5.6000
6.9000
3.5000
3.6000
2.9000
4.2000
6.1000
5.5000
6.6000
2.9000
3.3000
5.9000
6.0000
5.6000
>> y
y =
8.4000
11.7000
4.2000
6.1000
7.9000
10.2000
13.2000
6.6000
6.0000
4.6000
8.4000
12.0000
10.3000
13.3000
4.6000
6.7000
10.8000
11.5000
9.9000
计算代码:
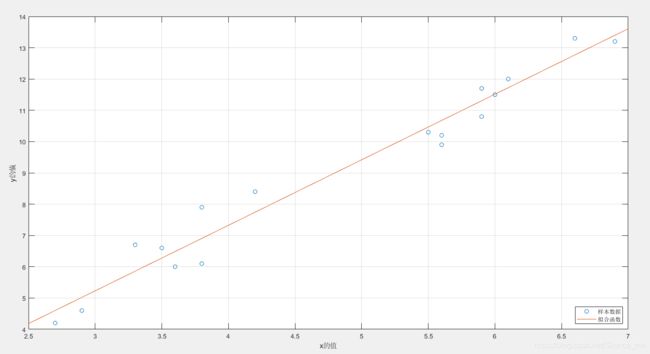
>> plot(x,y,'o')
>> % 给x和y轴加上标签
>> xlabel('x的值')
>> ylabel('y的值')
>> n = size(x,1);
>> k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
>> b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))
>> hold on % 继续在之前的图形上来画图形
>> grid on % 显示网格线
>> f=@(x) k*x+b; % 函数线
>> fplot(f,[2.5,7]); % 设置显示范围
>> legend('样本数据','拟合函数','location','SouthEast')
计算过程:
>> plot(x,y,'o')
>> % 给x和y轴加上标签
>> xlabel('x的值')
>> ylabel('y的值')
>> n = size(x,1);
>> n*sum(x.*y)-sum(x)*sum(y)
ans = 1.3710e+03
>> n*sum(x.*x)-sum(x)*sum(x)
ans = 654.4600
>> k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
k = 2.0948
>> b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))
b = -1.0548
>> hold on
>> grid on
>> f=@(x) k*x+b;
>> fplot(f,[2.5,7]);
>> legend('样本数据','拟合函数','location','SouthEast')
1.4 如何评价拟合的好坏
线性函数是指对参数为线性(线性于参数)
在函数中,参数仅以一次方出现,且不能乘以或除以其他任何的参数,并不能出现参数的复合函数形式。
1.5 证明SST = SSE + SSR
1.6 计算拟合优度的代码
>> y_hat = k*x+b; % y 的拟合值
>> SSR = sum((y_hat-mean(y)).^2) % 回归平方和
>> SSE = sum((y_hat-y).^2) % 误差平方和
>> SST = sum((y-mean(y)).^2) % 总体平方和
>> SST-SSE-SSR
>> R_2 = SSR / SST
计算过程:
>> y_hat = k*x+b; % y 的拟合值
>> SSR = sum((y_hat-mean(y)).^2) % 回归平方和
SSR = 151.1583
>> SSE = sum((y_hat-y).^2) % 误差平方和
SSE = 5.7281
>> SST = sum((y-mean(y)).^2) % 总体平方和
SST = 156.8863
>> SST-SSE-SSR
ans = 5.6843e-14
>> R_2 = SSR / SST
R_2 = 0.9635
1.7 拟合工具箱
低版本的Matlab可以在命令窗口中直接输入”cftool”

1.8 补充的计算函数randi,rand,normrnd,roundn
1.8.1 randi(范围,行,列): 产生均匀分布的随机整数(i = int)
%产生一个1至10之间的随机整数矩阵,大小为2x5;
s1 = randi(10,2,5)
9 4 5 3 2
7 6 1 2 3
%产生一个-5至5之间的随机整数矩阵,大小为1x10;
s2 = randi([-5,5],1,10)
-1 -5 4 5 0 0 -2 4 -1 -4
1.8.2 rand(行,列): 产生0至1之间均匀分布的随机数
%产生一个0至1之间的随机矩阵,大小为1x5;
s3 = rand(1,5)
0.780252068321138 0.389738836961253 0.241691285913833 0.403912145588115 0.0964545251683886
%产生一个a至b之间的随机矩阵,大小为1x5; % a + (b-a) * rand(1,5); 如:a,b = 2,5
s4= 2 + (5-2) * rand(1,5)
2.39591987781901 4.82615177232646 4.86840362068941 3.72562578523540 2.17933862884147
1.8.3 normrnd(均值,标准差,行,列):产生正态分布的随机数
%产生一个均值为0,标准差(方差开根号)为2的正态分布的随机矩阵,大小为3x4;
s5 = normrnd(0,2,3,4)
-1.73093606110961 -2.66400884263049 0.667021666131612 -0.260569306291441
-0.353068228462902 -4.65973431161015 0.782707208865802 0.367378191723884
1.58283212325727 -2.89819458567748 0.903358837856475 -0.952306033238148
1.8.4 roundn(数,位数)—任意位置四舍五入
% 0个位 1十位 2百位 -1小数点后一位 以此类推
a = 3.1415
roundn(a,-2) % ans = 3.1400
roundn(a,2) % ans = 0
a =31415
roundn(a,2) % ans = 31400
roundn(5.5,0) %6
roundn(5.5,1) %10
参考链接