神经网络预测模型基本原理与编程实现

原理

数据归一化

• 把数据经过处理后使之限定在一定的范围内。比如通常限制在区间[0, 1]或者[-1, 1]

为什么要归一化？

• 奇异样本数据：指相对于其他输入样本特别大或特别小的样本矢量
• 奇异样本数据的存在会引起训练时间增大，并可能无法收敛。所以在存在奇异样本数据的情况下，进行训练之前最好进行归一化，如果不存在奇异样本数据，则可以不用归一化。

归一化常用方法

网络设计

输入输出层设计

模型输入层节点数为输入特征数，输出层节点数为想要得到结果的个数。

隐层设计

• 只要隐节点足够多, 就可以以任意精度逼近一个非线性函数。
• 在网络设计过程中, 隐层神经元数的确定十分重要。隐层神经元个数过多, 会加大网络计算量并容易产生过度拟合问题; 神经元个数过少, 则会影响网络性能, 达不到预期效果。网络中隐层神经元的数目与实际问题的复杂程度、输入和输出层的神经元数以及对期望误差的设定有着直接的联系。
• 目前, 对于隐层中神经元数目的确定并没有明确的公式, 只有一些经验公式, 神经元个数的最终确定还是需要根据经验和多次实验来确定
• 经验公式： $l=\sqrt{n+m}+a$
  其中, n为输入层神经元个数, m为输出层神经元个数,a为[1,10]之间的常数。

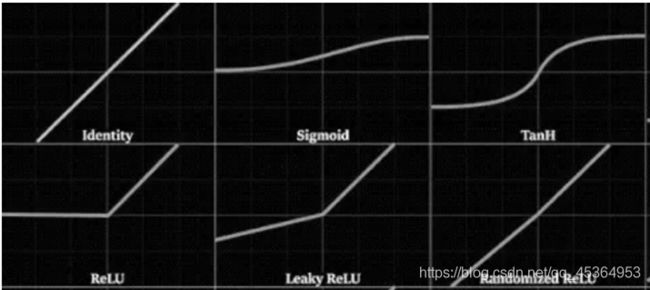
激活函数的选取

在神经网络中,激活函数的作用是能够给神经网络加入一些非线性因素,使得神经网络可以更好地解决较为复杂的问题。

神经网络训练效果评价

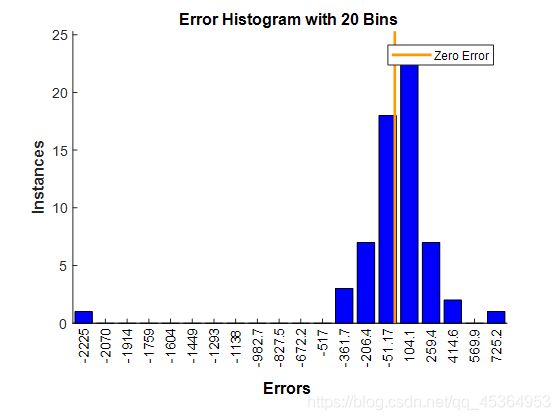
• 误差直方图
• 混淆矩阵（confusion matrix）
  混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目。
• ROC曲线：与混淆矩阵相同，也用来表征该神经网络的效果
  若训练效果不理想，可以选择Retrain

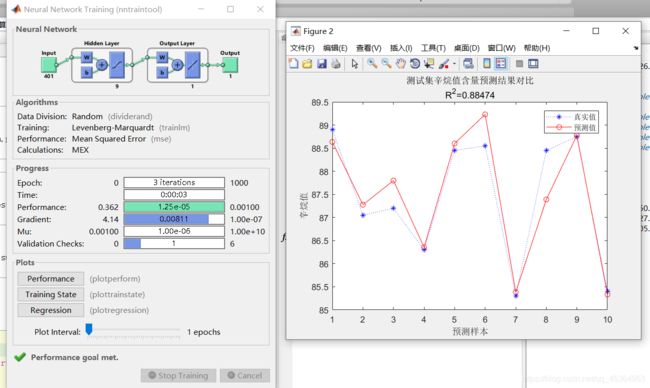
matlab工具箱

• epoch：其代表着迭代次数。BP神经网络的训练是采用迭代训练的，图中显示训练（迭代）15次即停止。特别的，右边的1000意思是训练次数上限为1000次，超过1000次自动停止。
• time：训练的时间。
• validation checks：与performance和gradient同为停止条件之一。但是通过performance和gradient停止意味着该神经网络达到了我们的预期，而通过validation checks停止则意味着该神经网络没有达到了我们的预期。

BP神经网络

• BP网络（Back-ProPagation Network）又称反向传播神经网络， 通过样本数据的训练，不断修正网络权值和阈值使误差函数沿负梯度方向下降，逼近期望输出。
• 它是一种应用较为广泛的神经网络模型，多用于函数逼近、模型识别分类、数据压缩和时间序列预测等。
• BP网络具有高度非线性和较强的泛化能力，但也存在收敛速度慢、迭代步数多、易于陷入局部极小和全局搜索能力差等缺点。

RBF神经网络

RBF神将网络是一种三层神经网络，其包括输入层、隐层、输出层。从输入空间到隐层空间的变换是非线性的，而从隐层空间到输出层空间变换是线性的。

RBF神经网络与BP神经网络之间的区别

• 1、局部逼近与全局逼近
  　　BP神经网络的隐节点采用输入模式与权向量的内积作为激活函数的自变量，而激活函数采用Sigmoid函数。各调参数对BP网络的输出具有同等地位的影响，因此BP神经网络是对非线性映射的全局逼近。
  　　RBF神经网络的隐节点采用输入模式与中心向量的距离（如欧式距离）作为函数的自变量，并使用径向基函数（如Gaussian函数）作为激活函数。神经元的输入离径向基函数中心越远，神经元的激活程度就越低（高斯函数）。RBF网络的输出与部分调参数有关，譬如，一个wij值只影响一个yi的输出（参考上面第二章网络输出），RBF神经网络因此具有“局部映射”特性。
• 局部逼近：指目标函数的逼近仅仅根据查询点附近的数据。
• 高斯径向基函数，函数图象是两边衰减且径向对称的，当选取的中心与查询点（即输入数据）很接近的时候才对输入有真正的映射作用，若中心与查询点很远的时候，欧式距离太大的情况下，输出的结果趋于0，所以真正起作用的点还是与查询点很近的点，所以是局部逼近
• 而BP网络对目标函数的逼近跟所有数据都相关，而不仅仅来自查询点附近的数据。
• 2、中间层数的区别
  　　BP神经网络可以有多个隐含层，但是RBF只有一个隐含层。
• 3、训练速度的区别
  　　使用RBF的训练速度快，一方面是因为隐含层较少，另一方面，局部逼近可以简化计算量。对于一个输入x，只有部分神经元会有响应，其他的都近似为0，对应的w就不用调参了。

BP神经网络实战

预测人口

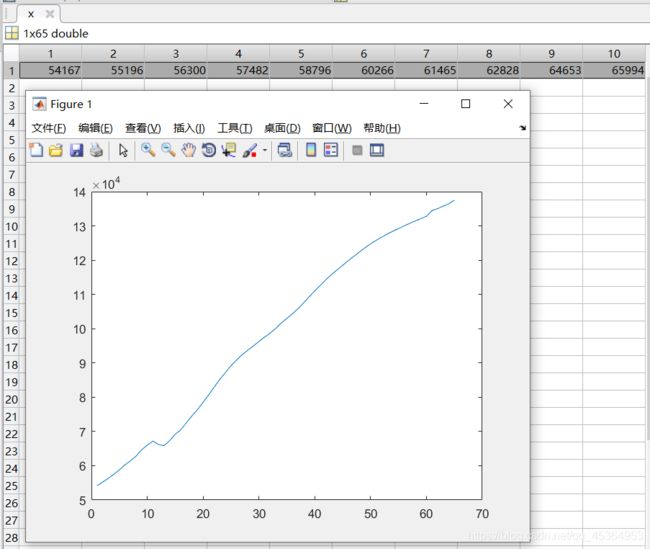
数据准备

注意x最后有个转置，变为行向量

% 清空环境变量
clear all
clc
% 输入数据，注意有个转置'
x=[54167    
55196    
56300    
57482    
58796    
60266    
61465    
62828    
64653    
65994    
67207    
66207    
65859    
67295    
69172    
70499    
72538    
74542    
76368    
78534    
80671    
82992    
85229    
87177    
89211    
 90859    
 92420    
 93717    
 94974    
 96259    
 97542    
 98705    
100072    
101654    
103008    
104357    
105851    
107507    
109300    
111026    
112704    
114333    
115823    
117171    
118517    
119850    
121121    
122389    
123626    
124761    
125786    
126743    
127627    
128453    
129227    
129988    
130756    
131448    
132129    
132802    
134480    
135030    
135770    
136460    
137510]';

自回归阶数：认为与前三年密切相关
input：训练网络的输入数据，shape为3行n-3列，表示这一年的人口只与前三年有关
inputs(:,i)=iinput(i:i+lag-1)’：第i+1年的人口由i~i+lag-1，这lag年的人口决定
targets=x(lag+1:end)：预测的目标结果

% 该脚本用来做神经网络预测
lag=3;    % 自回归阶数
iinput=x;    % x为原始序列（行向量）
n=length(iinput);

% 准备输入和输出数据
inputs=zeros(lag,n-lag);
for i=1:n-lag
    inputs(:,i)=iinput(i:i+lag-1)';
end
targets=x(lag+1:end);

网络构建与训练

fitnet函数在Matlab中的使用方法

% 创建网络
hiddenLayerSize = 10; %隐藏层神经元个数
net = fitnet(hiddenLayerSize);

% 避免过拟合，划分训练，测试和验证数据的比例
net.divideParam.trainRatio = 70/100;
net.divideParam.valRatio = 15/100;
net.divideParam.testRatio = 15/100;

%训练网络
[net,tr] = train(net,inputs,targets);

画图显示训练效果

%% 根据图表判断拟合好坏
yn=net(inputs);
errors=targets-yn;
figure, ploterrcorr(errors)                      %绘制误差的自相关情况（20lags）
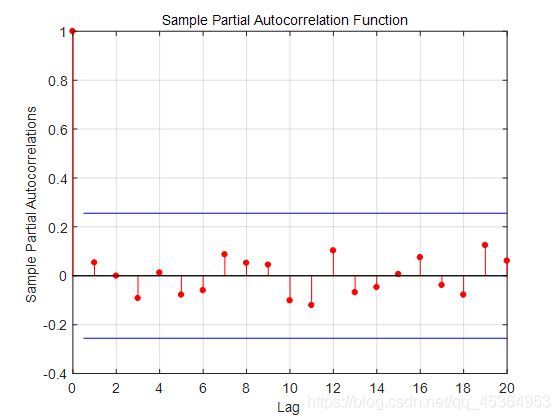
figure, parcorr(errors)                          %绘制偏相关情况
% [h,pValue,stat,cValue]= lbqtest(errors)         %Ljung－Box Q检验（20lags）
figure,plotresponse(con2seq(targets),con2seq(yn))   %看预测的趋势与原趋势
figure, ploterrhist(errors)                      %误差直方图
figure, plotperform(tr)                          %误差下降线

训练时的迭代效果：

回归系数（越接近1越好）：

自相关误差：

自相关性图中除了0阶自相关外，其他的自相关系数系数都不应该超过上下置信区间。

预测结果

预测未来7年的人口
注意f_in的更新方法，将预测得到的数据做为历史数据再进行预测
f(1) = net([iinput(n-2), iinput(n-1), iinput(n)])
f(2) = net([iinput(n-1), iinput(n), f(1)]
f(3) = net([ iinput(n), f(1), f(2)]
f(4) = net([f(1), f(2), f(3)]
…

%% 下面预测往后预测几个时间段
fn=7;  %预测步数为fn
f_in=iinput(n-lag+1:end)';	%取最后lag个数
f_out=zeros(1,fn);  %预测输出
% 多步预测时，用下面的循环将网络输出重新输入
for i=1:fn
    f_out(i)=net(f_in);	%预测第i年的人口
    f_in=[f_in(2:end);f_out(i)];	% 将预测出的第i年人口当作历史数据输入
end
% 画出预测图
figure,plot(1949:2013,iinput,'b',2013:2020,[iinput(end),f_out],'r')

预测汽油辛烷含量值

数据集中包含采集到的60组汽油样品，利用傅立叶近红外变换光谱仪对其进行扫描，扫描间隔为2nm的近红外光谱曲线如图所示，其中包含对曲线的局部放大图。同时数,每个样品的光谱曲线包含401个波长点，样品据集中包含使用传统的检测方法测定的辛烷含量值。

数据

%% I. 清空环境变量
clear all
clc

%% II. 训练集/测试集产生
%%
% 1. 导入数据
load spectra_data.mat

%%
% 2. 随机产生训练集和测试集
temp = randperm(size(NIR,1));
% 训练集——50个样本
P_train = NIR(temp(1:50),:)';
T_train = octane(temp(1:50),:)';
% 测试集——10个样本
P_test = NIR(temp(51:end),:)';
T_test = octane(temp(51:end),:)';
N = size(P_test,2);

%% III. 数据归一化
[p_train, ps_input] = mapminmax(P_train,0,1);
p_test = mapminmax('apply',P_test,ps_input);

[t_train, ps_output] = mapminmax(T_train,0,1);

网络

%% IV. BP神经网络创建、训练及仿真测试
%%
% 1. 创建网络
net = newff(p_train,t_train,9);

%%
% 2. 设置训练参数
net.trainParam.epochs = 1000;
net.trainParam.goal = 1e-3;
net.trainParam.lr = 0.01;

%%
% 3. 训练网络
net = train(net,p_train,t_train);

%%
% 4. 仿真测试
t_sim = sim(net,p_test);

%%
% 5. 数据反归一化
T_sim = mapminmax('reverse',t_sim,ps_output);

性能评价

决定系数越接近1越好

%% V. 性能评价
%%
% 1. 相对误差error
error = abs(T_sim - T_test)./T_test;

%%
% 2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2)); 

%%
% 3. 结果对比
result = [T_test' T_sim' error']

%% VI. 绘图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)

也可以使用径向基网络训练

net = newrbe(P_train, T_train, 30);