python简单实现 反向传播算法
1 一些铺垫
1、本文所使用例子来自于《一文弄懂神经网络中的反向传播法——BackPropagation》
![]()
I1,I2是输入层,h1,h2是隐含层,o1,o2是输出层,b1,b2是偏置。
其中,输入数据 i1=0.05,i2=0.10;
输出数据 o1=0.01,o2=0.99;
初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30; w5=0.40,w6=0.45,w7=0.50,w8=0.55
目标:给出输入数据i1,i2(0.05和0.10),使输出尽可能与原始输出o1,o2(0.01和0.99)接近。
2、本文所使用的反向传播算法的公式,都是来自吴恩达的神经网络与深度学习视频。
2 前向传播与反向传播
设代价函数为
![]()
其中A为预测值,Y为输出值。
由上面两层神经网络的的图片可以得到正向传播的步骤如下(上标代表所在神经元的层数):
![]()
![]()
![]()
3 python代码实现
import numpy as np
from matplotlib import pyplot as plt
# 设置中文可以显示
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
# 变量的定义
# 权重和偏置
W1=np.array([[0.15,0.20],[0.25,0.30]])
b1=0.35 # 因为有广播机制,所以不用写成向量形式
W2=np.array([[0.40,0.45],[0.50,0.55]])
b2=0.6
# 输入
X=np.array([[0.05],[0.10]])
# 输出
Y=np.array([[0.01],[0.99]])
# 学习率
alpha=0.5
# 迭代次数
Count=10000
# 样本个数
m=2
def sigmoid(x):
return 1/(1+np.exp(-x))
# 神经网络的训练
def NNtraining(W1,X,b1,W2,b2,Y,m,alpha):
Count=1000
J = np.zeros((Count, 1))
for i in range(Count):
# 前向传播
Z1 = np.dot(W1, X) + b1
A1 = sigmoid(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)
# 代价函数计算
J[i]=-1/m*(np.dot(Y.T,np.log(A2)+np.dot((1-Y).T,np.log(1-A2))))
# 反向传播
dZ2=A2-Y
dW2=1/m*np.dot(dZ2,A1.T)
db2=1/m*np.sum(dZ2,axis=1,keepdims=True)
dZ1=np.dot(W2.T,dZ2)*np.dot(Z1.T,1-Z1)
dW1=1/m*np.dot(dZ1,X.T)
db1=1/m*np.sum(dZ1,axis=1,keepdims=True)
# 梯度下降
W1=W1-alpha*dW1
b1=b1-alpha*db1
W2=W1-alpha*dW2
b2=b2-alpha*db2
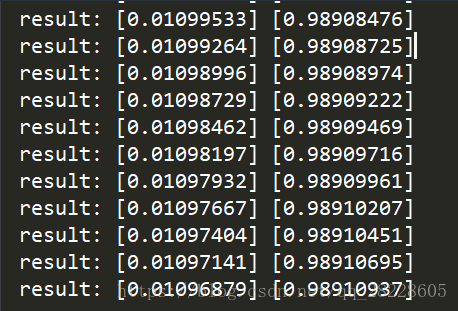
print("result:",A2[0],A2[1])
return J
if __name__ == '__main__':
# W1,X,b1,W2,b2,Y,m,alpha=InitNN()
J=NNtraining(W1,X,b1,W2,b2,Y,m,alpha)
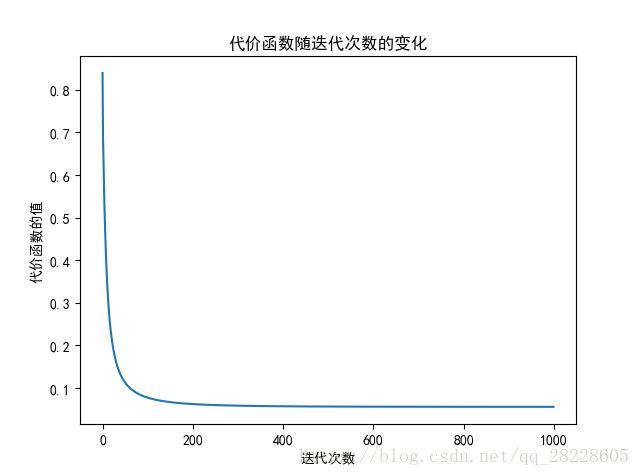
fig=plt.figure(1)
plt.plot(J)
plt.title(u'代价函数随迭代次数的变化')
plt.xlabel(u'迭代次数')
plt.ylabel(u'代价函数的值')
plt.show()