李宏毅2020机器学习05 - Logistic Regression

上节课提到在使用Generative model，且假设样本点服Gaussian distribution的情景下做Classification，后验概率P(C1|x) = $\sigma (w\cdot x+b)$，此时我们需要先找到$N_1,N_2,{\mu }^1,{\mu }^2,\Sigma$，再去找参数w和b。但我们希望直接找到参数w和b，这节课将提供解答。

Logistic Regression（逻辑回归）

步骤一：寻找model

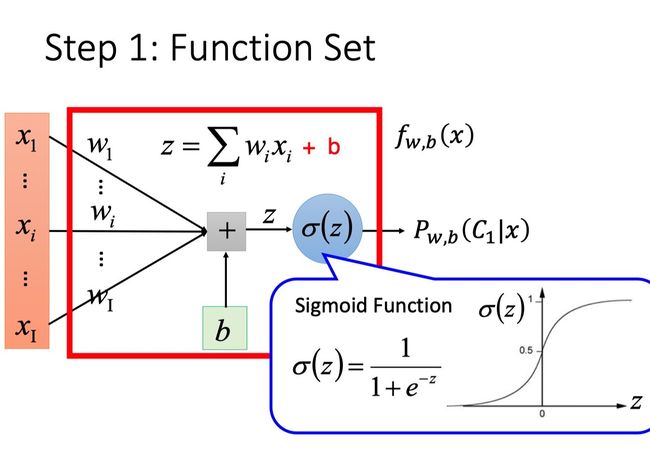
我们想要找到model：$P_{w,b}\left(C_1\mid x\right)$，当$P_{w,b}\left(C_1\mid x\right)\ge 0.5$时输出类型为class1，反之输出class2 。

又因为$$P_{w,b}\left(C_1\mid x\right)=\sigma (z)=\frac{1}{1+e^{-z}}$$ $$z=w\cdot x+b=\sum _i{w}_i{x}_i+b$$

这里的w和x都是vector，x_i代表不同的feature，而w_i对应不同feature的权重，对于每一个x_i，都对应一个w_i。

因此model可以进一步写成：$f_{w,b}(x)=P_{w,b}\left(C_1\mid x\right)=\sigma ({\sum }_i{w}_i{x}_i+b)$，它包含了w和b的所有可能性。

从上式我们可以看出，model是受w和b控制的。我们不必要像上节课一样计算一大堆东西，而是直接利用这个全新的由w和b决定的model——「Logistic Regression」。

注：在高斯分布的情景下考虑class1和class2共用Σ，可以得到一个线性的z，但是很多其他的概率分布模型也可以得到同样的结果：

$$P_{w,b}\left(C_1\mid x\right)=\sigma (z)=\frac{1}{1+e^{-z}}$$ $$z=w\cdot x+b=\sum _i{w}_i{x}_i+b$$

步骤二：找到loss function评估model好坏

已知model：$f_{w,b}(x)=P_{w,b}\left(C_1\mid x\right)=\sigma (w\cdot x+b)$

假设training data符合概率分布函数$f_{w,b}(x)$，且x¹属于class1，x²属于class1，x³属于class2，… ，x^N属于class1。

那么似然函数$L(w,b)=f_{w,b}\left(x^1\right)f_{w,b}\left(x^2\right)\left(1-f_{w,b}\left(x^3\right)\right)\cdots f_{w,b}\left(x^N\right)$。

当参数满足w=w^*,b=b^*时，取到最大似然估计值L(w^*,b^*)。

注：由于这里我们考虑的是二元分类问题，因此$f_{w,b}(x^3)=P_{w,b}\left(C_2\mid x^3\right)=1-f_{w,b}\left(x^3\right)$。

这次我们使用的是Logistic Regression而不是Gaussian distribution，因此不能再直接用平均值来求w^*和b^*，从而得到$L(w,b)$最大值。

由于$L(w,b)$是乘积形式，为了方便计算，我们作如下变换：

$$w^{\ast },b^{\ast }=\arg \underset{w,b}{\max }L(w,b)=\arg \underset{w,b}{\min }(-\ln L(w,b))$$

其中$$-\ln L(w,b)=-\ln f_{w,b}\left(x^1\right)-\ln f_{w,b}\left(x^2\right)-\ln \left(1-f_{w,b}\left(x^3\right)\right)-\dots$$

由于class1和class2的概率表达式不统一，上面的式子无法写成统一的形式。为统一格式，这里将所有training data打上0和1的标签。class1对应的label为1，class2对应的label为0 。$td:model真的只输出0和1吗？$

于是我们可以将上述式子进一步写成：

$$\begin{array}{rl}-\ln L(w,b)=& -\left[{\hat{y}}^1\ln f_{w,b}\left(x^1\right)+\left(1-{\hat{y}}^1\right)\ln \left(1-f_{w,b}\left(x^1\right)\right)\right]\\ & -\left[{\hat{y}}^2\ln f_{w,b}\left(x^2\right)+\left(1-{\hat{y}}^2\right)\ln \left(1-f_{w,b}\left(x^2\right)\right)\right]\\ & -\left[{\hat{y}}^3\ln f_{w,b}\left(x^3\right)+\left(1-{\hat{y}}^3\right)\ln \left(1-f_{w,b}\left(x^3\right)\right)\right]\\ & -\dots \end{array}$$

现在有了统一的格式，我们就可以「把要求最小值的对象写成和的形式」：

$$-\ln L(w,b)=\sum _n-\left[{\hat{y}}^n\ln f_{w,b}\left(x^n\right)+\left(1-{\hat{y}}^n\right)\ln \left(1-f_{w,b}\left(x^n\right)\right)\right]$$

实际上这表示的就是两个「伯努利分布」的交叉熵$H(p,q)=-{\sum }_{x}p(x)\ln (q(x))$。

交叉熵的含义是表达这两个分布有多么接近，如果p(x)和q(x)是一模一样的分布，那么它们的交叉熵就是0 。这里的$\hat{y}$代表理想的target，f(xⁿ)代表model的输出，把交叉熵放在这里就是想衡量$\hat{y}$和f(xⁿ)的分布之间的关系，我们希望他们的关系越接近越好，最好就是0 。

此刻，我们将交叉熵函数作为model的loss function。

步骤三：追寻最好的function

和上节课不同，这次我们可以对loss function进行微分，这就代表了我们可以用Gradient Descent来更新参数，找到最好的function，也就是找到w^*和b^*。$td：b不是scalr吗，怎么更新？$

我们会发现Gradient Descent的每次update只需要做：

$$w_i=w_i-\eta \sum _n-\left({\hat{y}}^n-f_{w,b}\left(x^n\right)\right)x_i^n$$

这个式子意味着每次的update只取决于三件事：

• 学习速率lr（这是你自己定的）
• x_i（来自于data）
• ${\hat{y}}^n-f_{w,b}\left(x^n\right)$，代表model的输出与理想target之间的差距，差距越大，update的步距就越大。

Logistic Regression和Linear Regression的区别

step1：

• logistic regression的输出介于0~1之间（因为它是借助sigmoid函数输出的）
• liner regression的输出可以是任何值

step2：

• logistic regression
  • 用输出1代表class1，输出0代表class2
  • 用交叉熵函数代表loss function
• liner regression
  • 输出是一个real number
  • 对差值的平方求均值，用来代表loss function

step3：

logistic regression和liner regression更新w_i的方式一模一样。唯一区别是logistic regression的$\hat{y}$取值介于0、1之间。

logistic regression + square error

上面我提到logistic regression采用的loss function和linear regression不同。但实际上，我们loss function选什么完全是可以由我们自己决定的。那么我们为什么选择用交叉熵来做logistic regression的loss function呢？为了对其作出解释，我们现在尝试不用交叉熵，而选择$L(f)=\frac{1}{2}{\sum }_n{\left(f_{w,b}\left(x^n\right)-{\hat{y}}^n\right)}^2$作为loss function。

机器学习的三个步骤：

现在会遇到一个问题：如果第n个点的target是class1，即$\hat{y}$=1，此时如果function的输出$f_{w,b}\left(x^n\right)=1$，就说明现在离target很接近了，$f_{w,b}\left(x^n\right)-{\hat{y}}^n$这一项等于0，于是微分$\partial L/\partial w_i=0$，这是很合理的。但是如果$f_{w,b}\left(x^n\right)=0$，这就说明离target很远，但是微分$\partial L/\partial w_i$仍旧等于0，这就不合理了。

对于class2的，得到的结果与class1一致。

如果我们把参数的变化对totol loss作图的话，loss function选择cross entropy和square error，参数的变化跟loss的变化情况可视化结果如下：

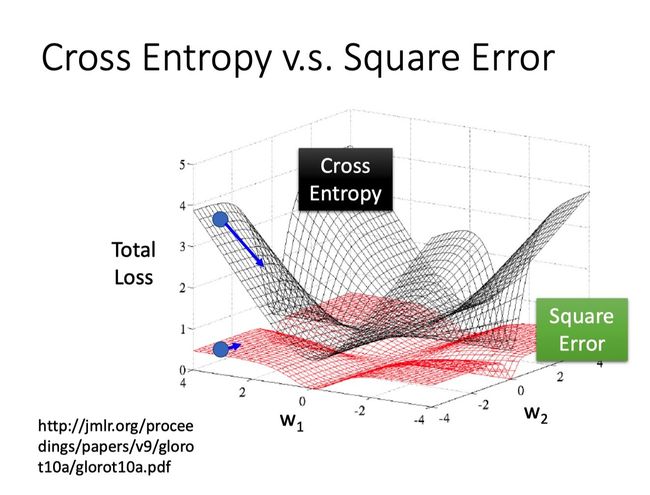
我们可以看到，对于square error，即使参数点所处位置与目标点很远，它的微分也很小，因此update的速度很慢。而对于cross entropy，离目标点很远的位置，参数微分很大，因此update速度很快。

这就是为什么在logistic regression中采用cross entropy而不是square error的原因。

Discriminative vs. Generative

Logistic Regression的方法，我们把它称之为Discriminative的方法；而我们用Gaussian来描述posterior Probability这件事，我们称之为Generative的方法。

他们采用的model都是一样的，都是$P\left(C_1\mid x\right)=\sigma (w\cdot x+b)$。但是Discriminative的方法是直接找w和b，而Generative的方法需要先找到${\mu }^1,{\mu }^2,{\Sigma }^{-1}$，再去找w和b。

同时，我们需要知道的是，两种不同的方法找到的w和b很可能是不同的。也就是说，我们采用的model一样，但是最终找到的function不见得是相同的。

这是因为在Logistic Regression里面，我们没有做任何实质性的假设，没有对Probability distribution有任何的描述，我们就是单纯地去找b和w（推导过程中的假设只是便于理解和计算，对实际结果没有影响）。
而在Generative model里面，我们对Probability distribution是有实质性的假设的，我们假设的是Gaussian，甚至假设在相互独立的前提下是否可以是naive bayes（朴素贝叶斯），根据这些假设我们才找到最终的b和w。
哪一个假设的结果是比较好的呢？ Generative model和discriminative model的预测结果比较如下:

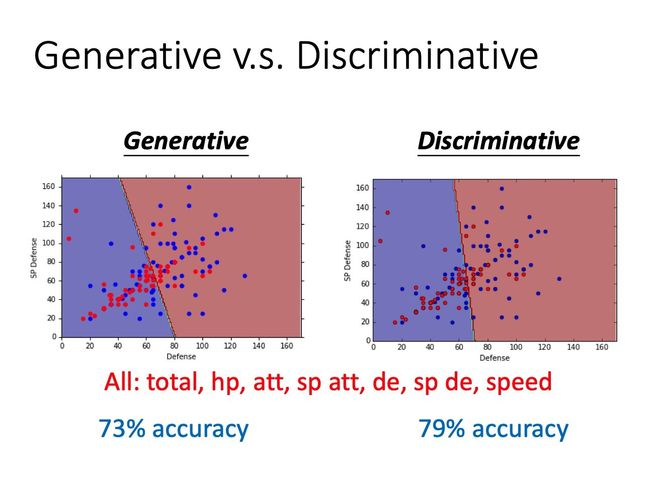
可以看到Discriminative的结果比Generative好。

这是因为Discriminative是「不含任何假设」的，而Generative「假设了你的data来自某个概率模型」。

而这种「假设」可能会损害model的performance。

比如下面这个例子：

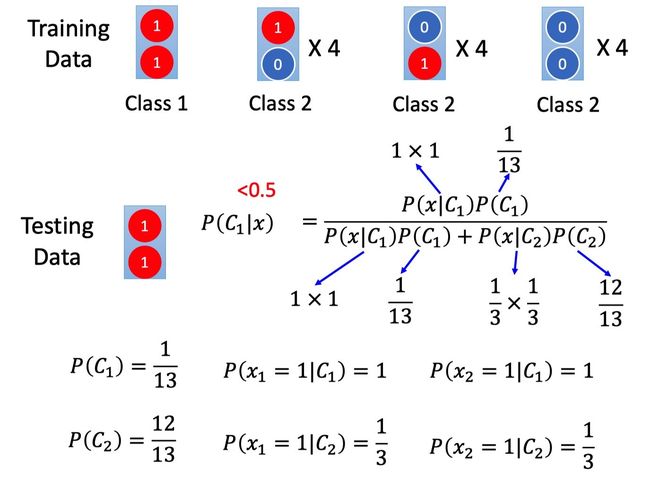
我们假设一笔testing data，它含有两个都是值为1的feature，现在判断它来自于class1和来自于class2的可能性哪个比较大。我们的直觉告诉我们，它来自于class1，因为class1中有一笔data的两个feature x₁,x₂都是1 。但是我们假设training data来自于「朴素贝叶斯模型」那么经过计算你会发现，这笔testing data是来自class2的。

因为当你有了「training data来自于「朴素贝叶斯模型」」这一假设，你就默认了feature x₁,x₂之间是相互独立的，你自己「脑补」了这种关系，因此你认为之所以在training data中我们没有看到x₁,x₂同为1却属于class2的data，是因为我们采样的点不够多，当你采样的点足够多，就会发现这笔testing data更可能属于class2 。

我们的直觉告诉我们「脑补」是不好的。这否就意味着Generative的方法不如Discriminative呢？如果不是，那么什么场景Generative model的表现更好？

Generative model表现较好的场景：

• training data较少时
  • Discriminative的performance是很依赖于data的，当data数量不足，或者data本身的label就有问题时，让Generative model做一些假设，反而可以把data不足或者label有问题带来的影响降到最低。
• 假设一种probability distribution对noise的鲁棒性会更好时
• Prior probability和class-dependent probabilities 能通过不同来源进行预测的时候
  • 比如语音辨识，你要预测某一句话被说出来的概率并不一定需要training data是有声音data，你也可以去网上爬取大量的文字，这样就可以计算出某一段文字出现的概率Prior probability，而对class-dependent的部分结合声音和文字去预测。这样处理可以把Prior probability预测的更加准确。$td$

多分类问题

之前讨论的都是二分类问题，现在探讨一下多分类问题。

假设有三个class：C1、C2、C3，三个类的分别对应不同的权重wⁱ和偏差b，我们通过softmax函数对其进行处理。

softmax函数作用：

• 对最大值做强化，拉开大小值之间的差距。
  • 因为在做第一步的时候，以e为底数，z为指数，使得大的值更大，小的值更小，拉开两者之间的差距。
• 实现给定一些数字，softmax函数就能将任意数字转化为概率。
• 在深度学习的CNN中，softmax层被作为多类分类问题的标准最终层，赋予CNN预测的能力。

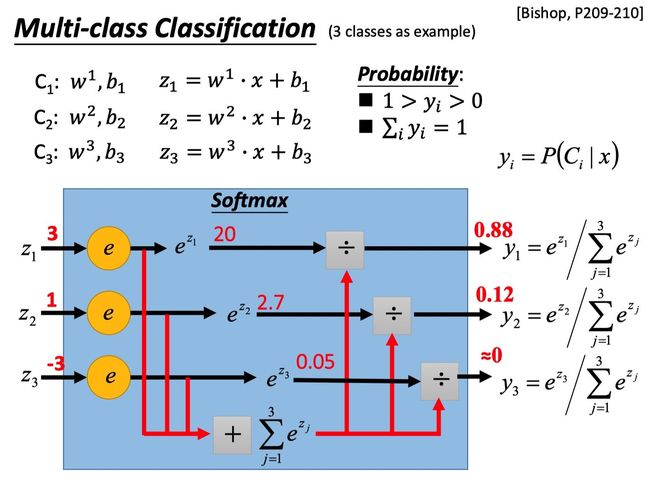
比如我们输入的z₁,z₂,z₃分别是3，1，-3。首先，我们计算e的指定数字zⁱ次方，然后将其所有结果相加，当作分母。最后，e的指定数字zⁱ次方作为分子，由此计算出后验概率y₁、y₂、y₃，分别表示输入x时，是class1、class2、class3的概率。且满足0 i <1,${\sum }_i{y}_i=1$。

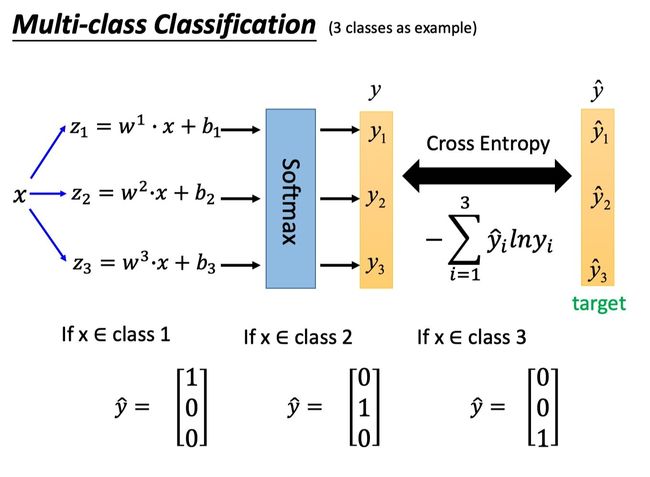
有了后验概率我们便可以像处理二分类问题一样，将输出y和target $\hat{y}$的交叉熵$-{\sum }_{i=1}^3{\hat{y}}_i\ln y_i$作为loss function，再作Gradient Descent得到最优function。

在做交叉熵的时候将3个class的label分别定为$\hat{y}=\left[\begin{array}{l}1\\ 0\\ 0\end{array}\right]\hat{y}=\left[\begin{array}{l}0\\ 1\\ 0\end{array}\right]\hat{y}=\left[\begin{array}{l}0\\ 0\\ 1\end{array}\right]$，这样就避免了像是定义3个class的label分别为1、2、3时，「假设了3个class之间，相邻class关系相差是一致的」的问题。

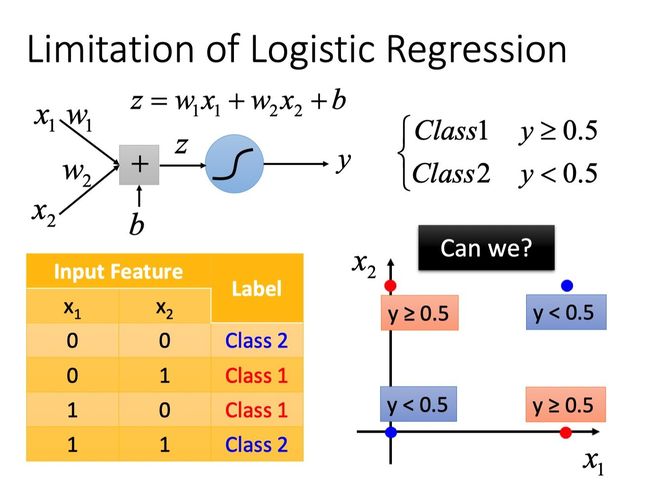
Logistic Regression的局限性

Logistic Regression其实存在很大的局限性，像是下面的情况，它就无法处理。因为在feature space上，它不能找到一条分界线，将class1和class2分到两个不同区域。

注：下图红点代表class1，蓝点代表class2.

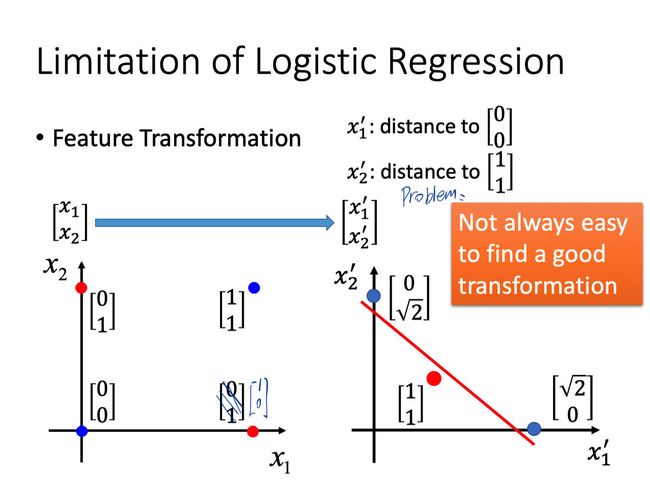
Feature Transformation

为了解决上述的问题，我们想到了对feature进行转换，比如将每个点的坐标x₁,x₂分别转换成到$\left[\begin{array}{l}0\\ 0\end{array}\right]$和$\left[\begin{array}{l}1\\ 1\end{array}\right]$的距离。

这样一来我们确实实现了将红点和蓝点划到分界线两边。但是这种需要人工去找的方法效率太低，况且我们不总是能找到好的转换方式。

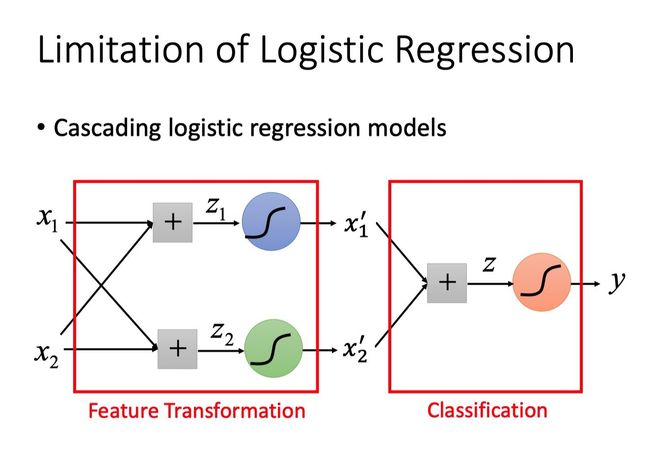
Cascading logistic regression models

为了让机器自己去做Feature Transformation，我们可以将regression model连接起来。

比如我们输入x₁、x₂，然后乘上它们各自的权重，得到z₁、z₂，再分别经过sigmoid function，得到$x_1^{\prime }$、$x_2^{\prime }$

。最后再接另外一个logistic regression，将$x_1^{\prime }$、$x_2^{\prime }$作为它的输入，在新的feature space上，我们就可以把class1和class2分开。

这里前两个model做的就是Feature Transformation，后面的model作为分类器。

注：为了简化model，我们这里不考虑bias。

通过改变权重参数，我们可以得到不同的$x_1^{\prime }$、$x_2^{\prime }$。

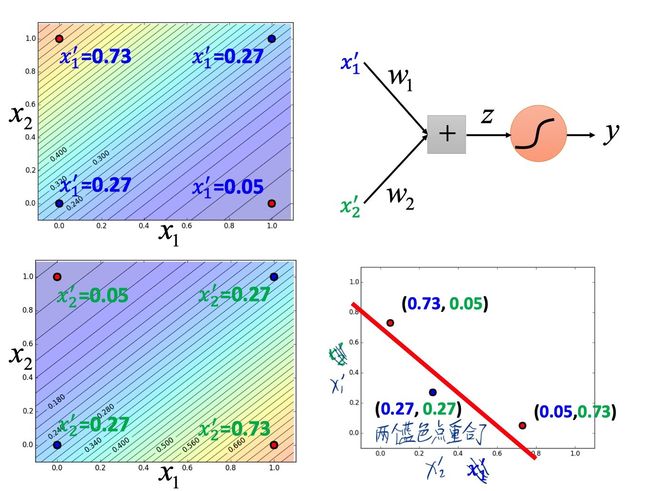
Logistic Regression的boundary一定是一条直线，它可以有任何的画法，但肯定是按照某个方向从高到低的等高线分布，具体的分布是由Logistic Regression的参数决定的，每一条直线都是由$z=b+{\sum }_i^n{w}_i{x}_i$组成的（二维feature的直线画在二维平面上，多维feature的直线则是画在多维空间上）。

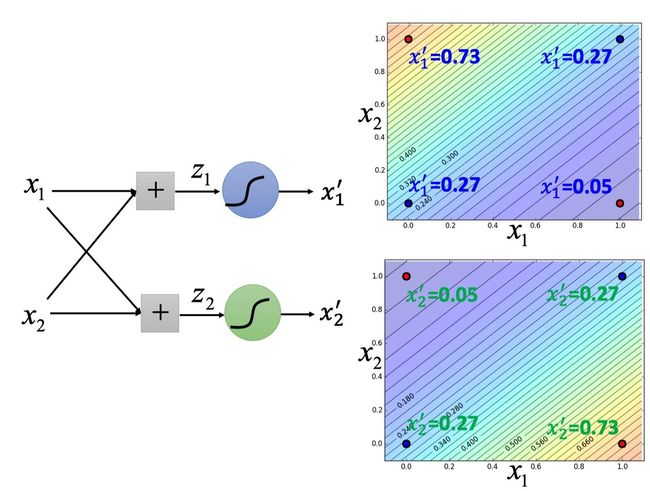
下图是二维feature的例子，分别表示四个点经过转换之后的$x_1^{\prime }$、$x_2^{\prime }$，在新的feature space中可以通过最后的Logistic Regression划分开来。

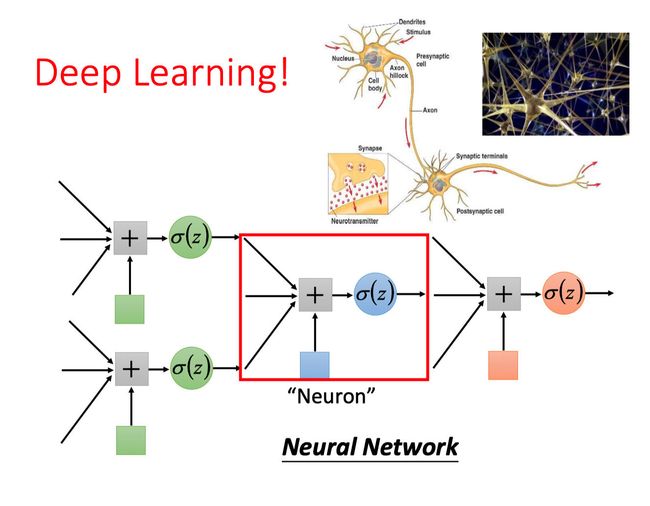
Deep Learning

事实上我们可以把每一个logistic regression model的输出当作令一个logistic regression model的输入，形成一个网状的结构。如果我们给每一个logistic regression model起一个新的名字——Neuron。那么它们形成的就是一个「类神经网络」，这东西就是Deep Learning。

Conclusion

对于分类的问题（主要是二元分类）我们可以用Generative model也可以用Logistic Regression，本质都是从「贝叶斯方程」出发，即
$$\begin{array}{rl}P\left(C_i\mid x\right)& =\frac{P\left(C_i\right)P\left(x\mid C_i\right)}{{\sum }_{j=1}^{n}P\left(C_j\right)P\left(x\mid C_j\right)}(1)\\ & =\sigma (z)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-\left(b+{\sum }_k{w}_k{x}_k\right)}}\end{array}(2)$$
其中分子表示属于x属于class i的可能性，分母表示所有可能性之和。

Generative model和Logistic Regression的区别在于「是否假设了某种概率分布」。由于Logistic Regression不存在「任何实质性假设」，因此只能通过公式(2)作为model进行分析。

对于多分类问题，引入softmax函数，用输出后验概率y_i构成的y与target $\hat{y}$做交叉熵，最后对交叉熵函数作梯度下降，得到最优function。