pytorch入门

一. 概念：张量、算子

张量：深度学习中表示和存储数据的主要形式。

即矩阵的扩展与延伸，可以认为是高阶的矩阵。1阶张量是向量，二阶张量是矩阵。与numpy的多维数组概念类似，可以具有任意多的维度。

算子：构建神经网络模型的基本组件。

深度学习算法由一个个算子组成，在网络模型中，算子对应层中的计算逻辑。

二. 使用pytorch实现张量运算
1.2 张量

import torch
#使用arange创建一个行向量x
x=torch.arange(12)
print(x)

1.2.1 创建张量
1.2.1.1 指定数据创建张量

import torch
import numpy as np
num=np.array([1,2,3])
#将num数组转化为tensor张量
num_tensor=torch.tensor(num)
print(num_tensor)

1.2.1.2 指定形状创建

import torch
import numpy as np
#创建2行3列的全零张量
num=torch.zeros([2,3])
print(num)

1.2.1.3 指定区间创建

import torch
import numpy as np
num_arange=torch.arange(start=1,end=3,step=1) #1~3不包括3
num_linspace=torch.linspace(start=1,end=3,steps=5) #1~5，共5个数
print(num_arange)
print(num_linspace)

1.2.2 张量的属性
1.2.2.1 张量的形状

import torch
import numpy as np
x=torch.ones([1,2,3,4])
print(x.ndim) #x的维度
4

print(x.shape) #x大小
torch.Size([1, 2, 3, 4])

print(x.shape[-1]) #最后一维大小
4

1.2.2.2 形状的改变

import torch
import numpy as np
num=np.array([[[1, 2, 3, 4, 5],
                        [6, 7, 8, 9, 10]],
                        [[11, 12, 13, 14, 15],
                         [16, 17, 18, 19, 20]],
                        [[21, 22, 23, 24, 25],
                         [26, 27, 28, 29, 30]]])
num_tensor=torch.tensor(num)
#改变张量形状，总数一致
num_tensor_reshape=torch.reshape(num_tensor,[2,3,5])
print('Before reshape:',num_tensor.shape)
print('After reshape:',num_tensor_reshape.shape)

1.2.2.3 张量的数据类型

整数会生成int 64。浮点数会生成float 32

import torch
import numpy as np
print(torch.tensor(0).dtype)
print(torch.tensor(0.0).dtype)
print(torch.zeros([2,2],dtype=torch.float32)) #指定浮点数类型

1.2.2.4 张量的设备位置

# 创建CPU上的Tensor
cpu_Tensor = torch.tensor(1, device=torch.device('cpu'))
print('cpu_Tensor:', cpu_Tensor.device)

运行结果
cpu_Tensor: cpu

 

1.2.3 张量与Numpy数组转换

import torch
import numpy as np
num=np.array([[1,2],[3,4]])
num_tensor=torch.tensor(num)
print(num_tensor)

1.2.4 张量的访问
1.2.4.1 索引和切片

import torch
import numpy as np
#生成张量
num= np.array([[1,2,3],[4,5,6]])
num_tensor = torch.tensor(num);
#索引:和普通的数组获取索引一样索引,对应的下标
for i in range(0, len(num_tensor)):
    print(num_tensor[i])
#切片：和普通的数组切片一样,start stop step
print(num_tensor[0:1:])

1.2.4.2 访问张量

import torch
import numpy as np
num= np.array([[1,2,3],[4,5,6]])
num_tensor = torch.tensor(num);
print(num_tensor[0]) #访问第一维
print(num_tensor[1,1]) #访问第一维第二个数字
print(num_tensor[1:]) #访问第一维的所有数字

 1.2.4.3 修改张量

import torch
import numpy as np
num=np.array([[1,2,3],[4,5,6]])
num_tensor=torch.tensor(num)
num_tensor[1,1]=1;
print('after change',num_tensor)

 

1.2.5 张量的运算

1.2.5.1 数学运算

import torch
import numpy as np
num=np.array([[1,2,3],[4,5,6]])
num_tensor=torch.tensor(num)
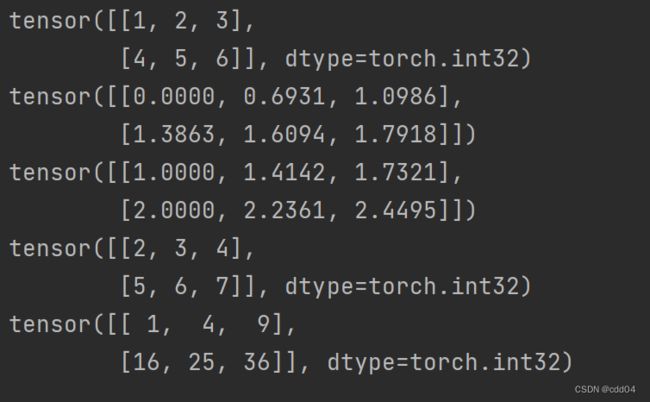
print(num_tensor.abs()) #取绝对值
print(num_tensor.log()) #取自然对数
print(num_tensor.sqrt()) #计算平方根
print(num_tensor.add(1)) #所有元素加一
print(num_tensor.pow(2)) #求平方

x.abs()                       # 逐元素取绝对值
x.ceil()                      # 逐元素向上取整
x.floor()                     # 逐元素向下取整
x.round()                     # 逐元素四舍五入
x.exp()                       # 逐元素计算自然常数为底的指数
x.log()                       # 逐元素计算x的自然对数
x.reciprocal()                # 逐元素求倒数
x.square()                    # 逐元素计算平方
x.sqrt()                      # 逐元素计算平方根
x.sin()                       # 逐元素计算正弦
x.cos()                       # 逐元素计算余弦
x.add(y)                      # 逐元素加
x.subtract(y)                 # 逐元素减
x.multiply(y)                 # 逐元素乘（积）
x.divide(y)                   # 逐元素除
x.mod(y)                      # 逐元素除并取余
x.pow(y)                      # 逐元素幂
x.max()                       # 指定维度上元素最大值，默认为全部维度
x.min()                       # 指定维度上元素最小值，默认为全部维度
x.prod()                      # 指定维度上元素累乘，默认为全部维度
x.sum()                       # 指定维度上元素的和，默认为全部维度

1.2.5.2 逻辑运算

x.isfinite()                  # 判断Tensor中元素是否是有限的数字，即不包括inf与nan
x.equal_all(y)                # 判断两个Tensor的全部元素是否相等，并返回形状为[1]的布尔类Tensor
x.equal(y)                    # 判断两个Tensor的每个元素是否相等，并返回形状相同的布尔类Tensor
x.not_equal(y)                # 判断两个Tensor的每个元素是否不相等
x.less_than(y)                # 判断Tensor x的元素是否小于Tensor y的对应元素
x.less_equal(y)               # 判断Tensor x的元素是否小于或等于Tensor y的对应元素
x.greater_than(y)             # 判断Tensor x的元素是否大于Tensor y的对应元素
x.greater_equal(y)            # 判断Tensor x的元素是否大于或等于Tensor y的对应元素
x.allclose(y)                 # 判断两个Tensor的全部元素是否接近

1.2.5.3 矩阵运算

import torch
import numpy as np
num_numpy = np.array([[1.0,2,3],[4,5,6]]) #需含浮点数
num_tensor = torch.tensor(num_numpy)
print(num_tensor.t()) #矩阵的转置
print(torch.transpose(num_tensor,1,0)) #交换第0维和第1维
print(torch.norm(num_tensor,p="fro")) #矩阵的弗洛贝尼乌斯范数
print(num_tensor.dist(num_tensor,p=2)) #矩阵(x-y)的2范数
print(num_tensor.matmul(num_tensor.t())) #矩阵乘法

 

1.2.5.4 广播机制

广播规则：

1）每个张量至少为一维张量。

2）从后往前比较张量的形状，当前维度的大小要么相等，要么其中一个等于1，要么其中一个不存在。

import torch
import numpy as np
x=torch.ones((1,2,3))
y=torch.ones((1,2,3))
z=x+y
print('broadcasting with two same shape tensor:',z.shape)
x1=torch.zeros((2,3,1,5))
y1=torch.zeros((3,4,1))
z1=x1+y1
print('broadcasting with two different shape tensor:',z1.shape)

三. 使用pytorch实现数据预处理
1. 读取数据集 house_tiny.csv、boston_house_prices.csv、Iris.csv

2. 处理缺失值

3. 转换为张量格式

import pandas as pd
import numpy as np
import torch

# 读取数据集
data_iris = pd.read_csv('Iris.csv')
data_house_tiny = pd.read_csv('house_tiny.csv')
data_boston_house_prices = pd.read_csv('boston_house_prices.csv')
# 处理缺失值和离散值
input, output = data_iris.iloc[:, 0:5], data_iris.iloc[:, 5]
# 使用均值处理缺失值
input = input.fillna(input.mean())
input = np.array(input)

# 处理离散值
output = pd.get_dummies(output, dummy_na=True)
output = np.array(output)
# 转换为张量形式
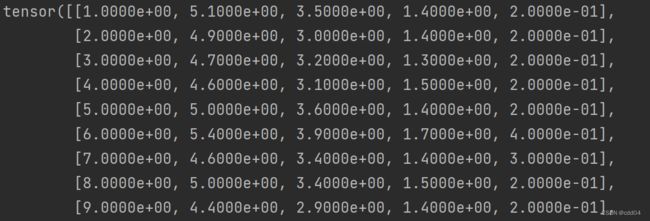
input_tensor, output_tensor = torch.tensor(input), torch.tensor(output)
print(input_tensor, output_tensor)
# 读取输入输出
input_house_tiny, output_house_tiny = data_house_tiny.iloc[:, 0:2], data_house_tiny.iloc[:, 2]
# 处理缺失值
input_house_tiny = input_house_tiny.fillna(input_house_tiny.mean())
# 处理离散值
input_house_tiny = pd.get_dummies(input_house_tiny, dummy_na=True)
input_house_tiny, output_house_tiny = np.array(input_house_tiny), np.array(output_house_tiny)
# 转换为张量形式
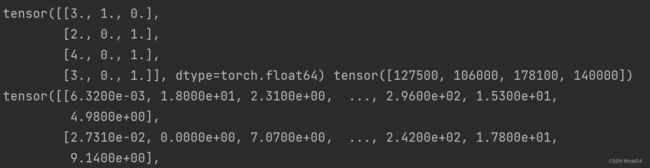
input_house_tiny_tensor, output_house_tiny_tensor = torch.tensor(input_house_tiny), torch.tensor(output_house_tiny)
print(input_house_tiny_tensor, output_house_tiny_tensor)

# 读取输出
input_boston_house_prices, output_boston_house_prices = data_boston_house_prices.iloc[:,
                                                        0:12], data_boston_house_prices.iloc[:, 12]
# 处理缺失值
input_boston_house_prices, output_boston_house_prices = input_boston_house_prices.fillna(
    input_boston_house_prices.mean()), output_boston_house_prices.fillna(output_boston_house_prices.mean())
# 转换为张量形式
input_boston_house_prices_numpy, output_boston_house_prices_numpy = np.array(input_boston_house_prices), np.array(
    output_boston_house_prices)
input_boston_house_prices_tensor, output_boston_house_prices_tensor = torch.tensor(
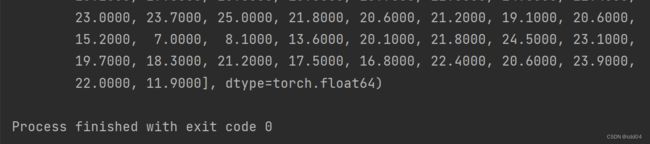
    input_boston_house_prices_numpy), torch.tensor(output_boston_house_prices_numpy)
print(input_boston_house_prices_tensor, output_boston_house_prices_tensor)

 

 

 

心得体会：了解了张量和算子的概念和属性，以及创建不同维度张量的多种方法；认识了一些tensor函数的用法，对数据处理也加深了印象。